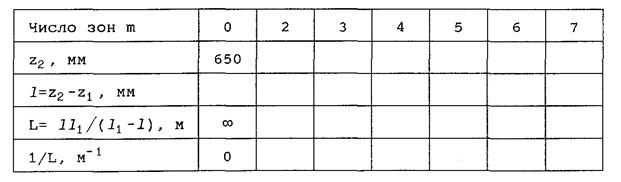
Дифракция в сходящейся волне
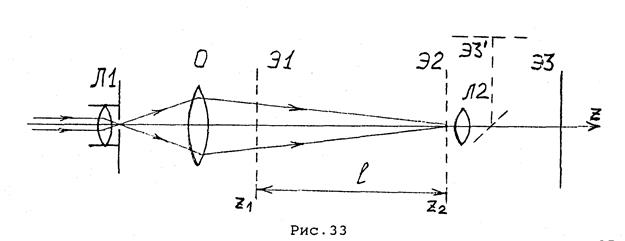
1. Схема опыта - та же (рис.47), однако теперь подберите положение объектива О так, чтобы волна сфокусировалась в плоскости Э2 (на экране фотоприемника Э3 получите яркую точку минимальных размеров, при этом модуль 3 должен быть в «стандартном» положении с координатой риски 650 мм). В итоге получаем схему по рис. 33.
 |
2. Помещайте в плоскости Э1 различные объекты. В плоскости Э2 и, соответственно, Э3 наблюдайте дифракционные картины Фраунгофера от этих объектов. Перепробуйте все объекты, что окажутся под рукой, как прилагаемые к установке, так и самодельные. Не забывайте размещать объекты на оси светового пучка.
4. Подвиньте экран Э1 возможно ближе к объективу и получите дифракционную картину Фраунгофера от круглого отверстия. Измерьте расстояние 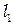 от экрана Э1 до фокуса волны. Оно потребуется нам для вычислений по формуле (70). Затем, перемещая модуль 3, приближайте плоскость Э2 к экрану Э1. При этом Вы будете получать дифракционные картины Френеля. Зафиксируйте и измерьте значения
от экрана Э1 до фокуса волны. Оно потребуется нам для вычислений по формуле (70). Затем, перемещая модуль 3, приближайте плоскость Э2 к экрану Э1. При этом Вы будете получать дифракционные картины Френеля. Зафиксируйте и измерьте значения 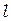 , при которых открыты
, при которых открыты 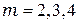 и т.д. зоны Френеля. Измеренные данные занесите в таблицы 1 и 2.
и т.д. зоны Френеля. Измеренные данные занесите в таблицы 1 и 2.
6. Постройте график зависимости 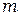 от
от 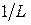 . Сравните теорией.
. Сравните теорией.
Таблица 1.
| Координата объекта Э1 | 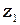 , мм. , мм. | |
| Координата плоскости наблюдения | 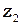 , мм. , мм. | |
| Координата фокальной плоскости волны | 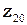 , мм. , мм. | |
| Расстояние от фокуса волны до экрана Э1 | 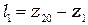 , мм. , мм. | |
| Диаметр отверстия | 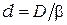 , мм. , мм. |
Таблица 2.
ЛАБОРАТОРНАЯ РАБОТА № 3.43 ДИФРАКЦИЯ ФРАУНГОФЕРА НА ПРЯМОУГОЛЬНОМ ОТВЕРСТИИ
Цель работы – Определение углов дифракции для минимумов на дифракционных картинах от прямоугольного отверстия.
Оборудование – модульный лабораторный учебный комплекс ЛКО-1.
Методика эксперимента
Наблюдение дифракции Фраунгофера на крупных объектов (более 0,1мм) без использования дополнительной оптики может потребовать слишком больших размеров установки. Поэтому, как правило, дифракционные картины Фраунгофера наблюдают в фокальной плоскости сходящейся сферической волны.
Пусть плоская волна нормально падает на экран Э1 (Рис. 50), а дифракционная картина наблюдается на экране Э2 в фокальной плоскости линзы Л. (Здесь сохранена нумерация рисунков и формул по учебному пособию - В. В. Светозаров. Модульный оптический практикум: Учебное пособие. М.: ВЛАДИС, 1998. 85 с.) Каждой точке Р в плоскости наблюдения соответствует определённое направление излучения, выходящего из плоскости Э1. Такое же соответствие мы получили бы без линзы Л, если бы удалили экран Э2 на расстояние 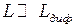 , где
, где 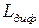 - дифракционная длина (расстояние Релея, см раздел 7.).
- дифракционная длина (расстояние Релея, см раздел 7.).
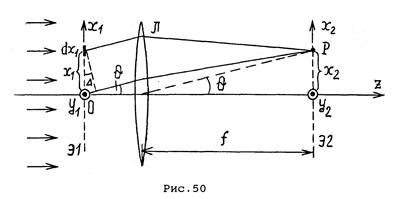
Амплитуда колебаний в точке Р, в соответствии с принципом Гюйгенса-Френеля, определяется амплитудами и фазами приходящих в эту точку волн, излучённых в соответствующем направлении всеми элементами экрана Э1. В простейшем случае амплитуды определяются коэффициентом пропускания экрана Э1, а фазы - разностью хода 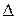 (рис. 50).
(рис. 50).
Такая схема позволяет упростить установку и более гибко варьировать параметры опыта, благодаря чему широко используется в современной когерентной оптике. Непосредственный расчёт дифракционной картины в сходящейся волне сложен, но можно воспользоваться результатами расчёта для классической схемы.
Рассмотрим ещё раз классическую схему (рис. 51а). Согласно принципу Гюйгенса - Френеля амплитуда колебаний в произвольной точке наблюдения Р экрана Э2 определяется амплитудами и фазами колебаний вторичных источников, расположенных на поверхности, отделяющей первичный источник от наблюдателя. Выберем в качестве такой поверхности плоскость 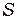 , расположенную сразу после линзы. Амплитуды и фазы колебаний в этой плоскости определяются коэффициентом пропускания экрана Э1 и оптической длиной лучей, идущих от источника до плоскости.
, расположенную сразу после линзы. Амплитуды и фазы колебаний в этой плоскости определяются коэффициентом пропускания экрана Э1 и оптической длиной лучей, идущих от источника до плоскости.
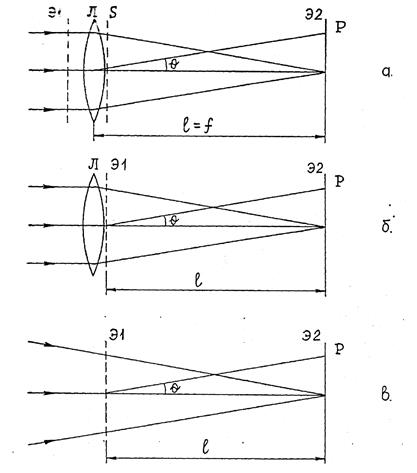
Рис. 51
Указанные амплитуды и фазы не изменятся, если экран Э1 расположить не перед линзой Л, а сразу после неё, совместив его с плоскостью S, как показано на рис.51б. Не изменится при этом и дифракционная картина на экране Э2. Теперь дифракционная картина полностью определяется экраном Э1 и падающей на него волной. Способ создания волны несуществен. Поэтому оптическая система, создающая сходящуюся волну, может быть какой угодно и расположена где угодно. На рис.51в эта система вынесена за пределы рисунка.
Зависимость интенсивности излучения на экране Э2 от положения точки Р, или, что то - же, от направления излучения, определяемого углом 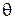 , в схеме по рис. 51в будет такой же, как и в классической схеме (рис. 50), с тем лишь различием, что во всех формулах вместо фокусного расстояния линзы
, в схеме по рис. 51в будет такой же, как и в классической схеме (рис. 50), с тем лишь различием, что во всех формулах вместо фокусного расстояния линзы 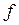 будет фигурировать расстояние
будет фигурировать расстояние 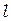 между экранами Э1 и Э2.
между экранами Э1 и Э2.
ПРЯМОУГОЛЬНОЕ ОТВЕРСТИЕ
Дифракционная картина от прямоугольного отверстия (рис.53) размером 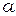 вдоль оси х1 и размером
вдоль оси х1 и размером 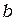 вдоль оси y1 имеет вид креста, состоящего из дифракционных максимумов. Большей стороне отверстия соответствует меньшая ширина максимума. Распределение интенсивности вдоль оси
вдоль оси y1 имеет вид креста, состоящего из дифракционных максимумов. Большей стороне отверстия соответствует меньшая ширина максимума. Распределение интенсивности вдоль оси 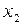 описывается выражением:
описывается выражением:
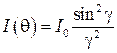 (76
(76
где 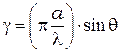 .
.
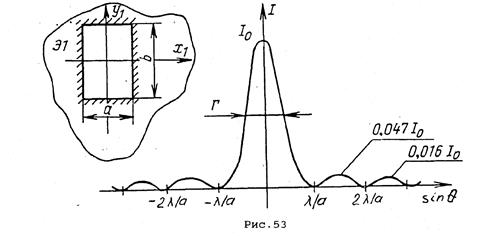
Условие минимумов интенсивности света в плоскости наблюдения ( 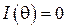 ) определяется формулой:
) определяется формулой:
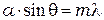 , (77)
, (77)
где 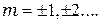 При малых
При малых 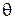 это условие эквивалентно выражению (64).
это условие эквивалентно выражению (64).
Распределение интенсивности света по оси 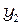 аналогично распределению по оси х2 и отличается лишь заменой размера
аналогично распределению по оси х2 и отличается лишь заменой размера 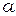 на размер
на размер 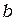 .
.
Порядок выполнения работы
1. Перед началом работы изучите общую теорию явления дифракции и дифракцию Фраунгофера на щели.
2. Изучите устройство и правила эксплуатации комплекса ЛКО-1 в Приложении 5.
3. Ознакомьтесь с порядком включения и выключения лазерного источника света и инструкцией по технике безопасности. Обратите особое внимание на недопустимость попадания в глаза прямого лазерного излучения.
4. Соберите на оптической скамье комплекса типичную схему для наблюдения интерференции и дифракции согласно рис. 33.
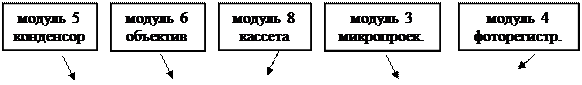 |

Параллельный пучок излучения лазера превращается конденсорной линзой Л1 и объективом О в сходящуюся волну, сфокусированную в объектной плоскости Э2 линзы Л2 микропроектора (модуль 3) с координатой риски 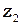 = 650 мм. При этом на экране фотоприемника Э3 (или Э3׳) видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой
= 650 мм. При этом на экране фотоприемника Э3 (или Э3׳) видна яркая точка малых размеров. Исследуемые объекты (щели, пары щелей) помещаются в кассете для экранов (модуль 8) в плоскости Э1 с координатой 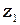 . При этом в плоскости Э2 образуется интерференционная или дифракционная картина, которая в увеличенном виде наблюдается на экране Э3.
. При этом в плоскости Э2 образуется интерференционная или дифракционная картина, которая в увеличенном виде наблюдается на экране Э3.
Для наблюдения и измерения параметров самих объектов их помещают в кассету в объектной плоскости линзы Э2 (модуль 3), а объектив О (модуль 5) смещают так, чтобы волна расфокусировалась и осветила всю поверхность объекта. При этом на экране фотоприёмника Э3 возникает увеличенное изображение объектов.
В схеме на рис. 33 и последующих вместо реального положения экрана Э3׳ показанного пунктиром, мы будем давать положение Э3, в котором игнорируется излом лучей зеркалом микропроектора.
3*. Включите лазерный источник света.
Внимание. Пункты, помеченные звёздочкой, выполняет преподаватель или лаборант.
Задание 1
1. Установите в кассету модуля 8 объект 20 с квадратным (2х2 мм) отверстием. Получите на экране Э3 увеличенную в 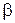 раз дифракционную картину, где
раз дифракционную картину, где 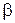 - увеличение микропроектора.
- увеличение микропроектора.
2. Рукоятками горизонтального и вертикального перемещения на модуле 8 расположите дифракционный “крест” вдоль координатных осей экрана Э3 и измерьте координаты нескольких (не менее 3 в каждом “луче” креста) минимумов. Данные занесите в таблицу.
Таблица 1.
| Объект 20 Отверстие 2х2 мм. | Объект 21 Отверстие 1х2 мм. | ||||||
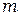 | 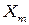 | 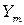 | 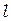 | 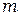 | 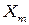 | 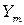 | 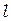 |
3. Аналогичные измерения сделайте для объекта 21 - прямоугольного отверстия 1х2 мм.
4. Установите объект 20 в кассету микропроектора (модуль 3) и, перемещая окуляр (модуль 6) получите увеличенное изображения квадратного отверстия. Определите увеличение микропроектора по формуле 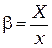 , где
, где 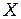 - размер изображения квадратного отверстия на экране Э3׳,
- размер изображения квадратного отверстия на экране Э3׳, 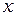 - реальный размер отверстия по паспорту 2х2 мм.
- реальный размер отверстия по паспорту 2х2 мм.
5. Определив реальный размер координат минимумов 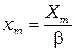 , рассчитайте углы дифракции
, рассчитайте углы дифракции 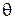 , соответствующие минимумам, и сравните с теоретическими, рассчитанными по формуле (77)
, соответствующие минимумам, и сравните с теоретическими, рассчитанными по формуле (77) 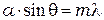 при
при 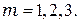 При расчёте экспериментального значения углов дифракции полагаем что
При расчёте экспериментального значения углов дифракции полагаем что 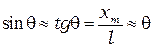 . Расчётные данные занесите в таблицу 2.
. Расчётные данные занесите в таблицу 2.
Таблица 2
