Моделирование случайных событий
В теории вероятностей реализацию некоторого комплекса условий называют испытанием. Результат испытания, регистрируемый как факт, называют событием.
Случайным называют событие, которое в результате испытания может наступить, а может и не наступить (в отличие от достоверного события, которое при реализации данного комплекса наступает всегда, и невозможного события, которое при реализации данного комплекса условий не наступает никогда). Исчерпывающей характеристикой случайного события является вероятность его наступления. Примерами случайных событий являются отказы в экономических системах; объемы выпускаемой продукции каждым предприятием в каждый день; котировки валют в обменных пунктах; состояние рынка ценных бумаг и биржевого дела и т. п.
Моделирование случайного события заключается в определении («розыгрыше») факта его наступления.
Для моделирования случайного события А, наступающего в опыте с вероятностью РА, достаточно одного случайного (псевдослучайного) числа R, равномерно распределенного на интервале [0; 1]. В случае попадания ПСЧ R в интервал [0; РА]событие А считают наступившим в данном опыте; в противном случае — не наступившим в данном опыте. На рис. 10.5 показаны оба исхода: при ПСЧ R1событие следует считать наступившим; при ПСЧ R2 — событие в данном испытании не наступило.
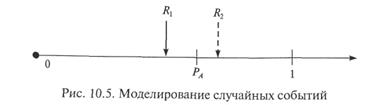
Очевидно, что чем больше вероятность наступления моделируемого события, тем чаще ПСЧ, равномерно распределенные на интервале [0; 1], будут попадать в интервал [0; РА],что и означает факт наступления события в испытании.
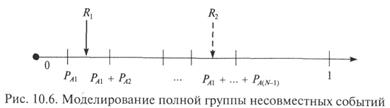
Для моделирования одного из полной группы N случайных несовместных событий А1, A2, ..., AN свероятностями наступления {PA1, РА2, ..., PAN}соответственно также достаточно одного ПСЧ R.
Для таких случайных событий можно записать
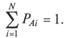
Факт наступления одного из событий группы определяют, исходя из условия принадлежности ПСЧ R тому или иному интервалу, на который разбивают интервал [0; 1]. Так, на рис. 10.6 для ПСЧ R1 считают, что наступило событие А2. Если ПСЧ оказалось равным R2, считают, что наступило событие A(N - 1).
Если группа событий не является полной, вводят дополнительное (фиктивное) событие A(N + 1), вероятность которого определяют по формуле
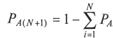
Далее действуют по уже изложенному алгоритму для полной группы событий с одним изменением: если ПСЧ попадает в последний (N + 1)-й интервал, считают, что ни одно из N событий, составляющих неполную группу, не наступило.
В практике имитационных исследований часто возникает необходимость моделирования зависимых событий, для которых вероятность наступления одного события оказывается зависящей от того, наступило или не наступило другое событие. В качестве одного из примеров зависимых событий приведем доставку груза потребителю в двух случаях: когда маршрут движения известен и был поставщиком дополнительно уточнен и когда уточнения движения груза не проводилось. Понятно, что вероятность доставки груза от поставщика к потребителю для приведенных случаев будет различной.
Для того чтобы провести моделирование двух зависимых случайных событий А и В, необходимо задать следующие полные и условные вероятности:
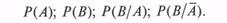
Заметим, что, если вероятность наступления события В при условии, что событие А не наступило, не задана, ее можно определить по формуле
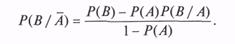
Существуют два алгоритма моделирования зависимых событий. Один из них условно можно назвать «последовательным моделированием»; другой — «моделированием после предварительных расчетов».
Последовательное моделирование.Алгоритм последовательного моделирования представлен на рис. 10.7.
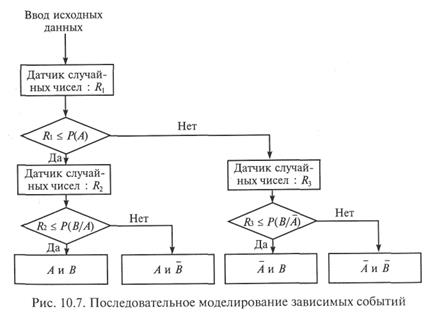
Несомненными достоинствами данного алгоритма являются его простота и естественность, поскольку зависимые события «разыгрываются» последовательно — так, как они наступают (или не наступают) в реальной жизни, что и является характерной особенностью большинства имитационных моделей. Вместе с тем алгоритм предусматривает троекратное обращение к датчику случайных чисел, что увеличивает время моделирования.
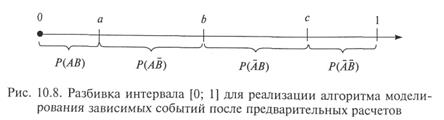
Моделирование после предварительных расчетов.Как легко заметить, приведенные на рис. 10.7 четыре исхода моделирования зависимых событий образуют полную группу несовместных событий. На этом основан алгоритм моделирования, предусматривающий предварительный расчет вероятностей каждого из исходов и «розыгрыш» факта наступления одного из них, как для любой группы несовместных событий. Рис. 10.8 иллюстрирует разбивка интервала [0; 1] на четыре отрезка, длины которых соответствуют вероятностям исходов наступления событий.
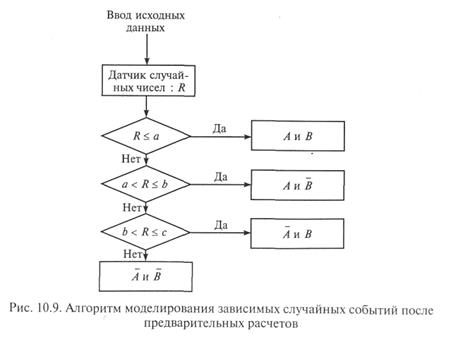
На рис. 10.9 представлен алгоритм моделирования. Данный алгоритм предусматривает одно обращение к датчику случайных чисел, что обеспечивает выигрыш во времени имитации по сравнению с последовательным моделированием, однако перед началом работы алгоритма исследователь должен рассчитать и ввести вероятности реализации всех возможных исходов (естественно, эту несложную процедуру можно также оформить программно, но это несколько удлинит алгоритм).