Алгоритм обратного распространения ошибки

Цель обучения состоит в том, чтобы достичь баланса между способностью сети давать верный отклик на входные данные, использовавшиеся в процессе обучения (запоминания), и способностью выдавать правильные результаты в ответ на входные данные, схожие, но неидентичные тем, что были использованы при обучении (принцип обобщения). Обучение сети методом обратного распространения ошибки включает в себя три этапа: подачу на вход данных, с последующим распространением данных в направлении выходов, вычисление и обратное распространение соответствующей ошибки и корректировку весов. После обучения предполагается лишь подача на вход сети данных и распространение их в направлении выходов. При этом, если обучение сети может являться довольно длительным процессом, то непосредственное вычисление результатов обученной сетью происходит очень быстро. Кроме того, существуют многочисленные вариации метода обратного распространения ошибки, разработанные с целью увеличения скорости протекания процесса обучения.

Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска. Для функционирования алгоритма Обратного распространения ошибки необходимо задать критерий окончания алгоритма. Основные критерии окончания алгоритма:

· Прошло необходимое количество итераций. Не эффективный способ, так как заранее неизвестно как много итераций необходимо для обучения сети

· Достигнута заданная точность. Более эффективный способ. Однако встает вопрос выбора необходимой точности. Слишком большое значение может привести к плохой работе сети, слишком маленькое значение к малой обобщающей способности или, возможно, сеть никогда не достигнет заданной точности.

· Изменение ошибки меньше заданной. Может означать что сеть слишком медленно обучается, так как попала в локальный минимум.

· Комбинация предложенных выше способов.

В тех случаях, когда удается оценить работу сети, обучение нейронных сетей можно представить, как задачу оптимизации. Оценить — означает указать количественно, хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех её параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:

Где Е – ошибка сети

L – Количество образов из обучающей выборки

N – Размерность выходных образов

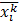– Значение, рассчитанное сетью

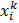– Эталонное значение

Для модификации настраиваемых параметров используется метод градиентного спуска. После каждого обучающегося примера необходимо подправлять веса. Чтобы добраться до минимума ошибки, необходимо двигаться в сторону, противоположную градиенту, то есть прибавлять к исходным весам

Где 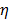– Коэффициент, задающий скорость обучения. Обычно принимается из диапазона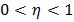

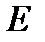— среднеквадратичная ошибка нейронной сети для одного образа. Она определяется, как ,где — эталонное выходное начение j-го нейрона. Ошибка j-го нейрона выходного слоя равняется: .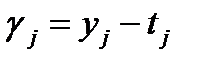

Для любого скрытого слоя 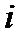ошибка 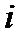-го нейронного элемента определяется рекурсивным образом через ошибки нейронов следующего слоя :

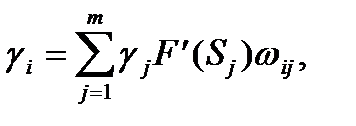
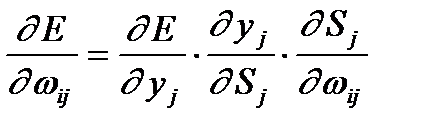
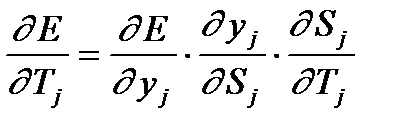
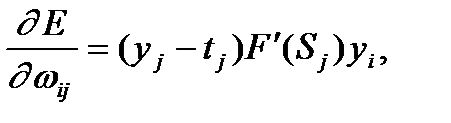
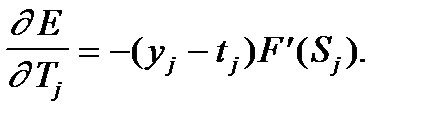
Где - вес между I и j нейроном.

- значение, рассчитанное на выходе j нейрона

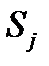- взвешенная сумма j нейрона

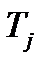- порог j нейрона

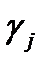- разность между эталонным и выходным значением

- производная функции активации.

Алгоритм выглядит следующим образом:

1) Инициализировать настраиваемые параметры (рекомендуется в достаточно узком диапазоне, например, (0,1)

2) Подать текущий образ на сеть

3) Рассчитать ошибку для каждого элемента

3.1) рассчитать ошибку выходного слоя

3.2) рассчитать ошибку скрытых слоев

4) Модифицировать настраиваемы параметры

5) Если есть ещё образы, то на шаг 2

6) Проверить условие завершения алгоритма обучения (например, рассчитать ошибку сети). Если условие не выполнено, на шаг 2

Несмотря на многочисленные успешные применения обратного распространения, оно не является универсальным решением. Больше всего неприятностей приносит неопределённо долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.

В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.

Анализ задания

Pixel Art можно также назвать “Рисунок символами». Люди используют рисунки символами по ряду причин. Вот некоторые из них.

1. Это самый универсальный вид компьютерного искусства в мире - каждый компьютер, система способна отображать рисунки символами без преобразования или специального программного обеспечения.

2. ASCII графика компактна, размер рисунков символами в сотни раз меньше размера файлов GIF или BMP, что даёт им преимущество перед обычными графическими форматами.

3. Это просто - скопировать из одного файла в другой (так же, вырезать и вставить).

4. Это интересно, увлекательно и эстетически красиво!

В результате выполнения курсовой работы должна быть разработана программа, позволяющая кодировать изображение в цветной текст. Для возможности вывода его в дальнейшем на Windows консоль необходимо предусмотреть вариант сведения всей цветовой палитры изображение к ограниченному множеству цветов, поддерживаемых в консоли. При этом критерием качества кодирования является не качество отображения отдельно взятого образа, а конечный результат. Кодирование является успешным если выходное текстовое поле схоже с входным изображением.

Рисунок 2.1: Пример входного изображения, и схожего выходного поля

Также необходима возможность применения алгоритмов предобработки до начала процесса кодирования. Например удаление цвета или фона.