Анализосновныхметодовпоиска

В данном разделе проводятся анализ и сравнение основных методов поиска. Вна­чале рассмотрим их применение для поиска в графах, затем прокомментируем опти­мальность вырабатываемых ими решений. Наконец, проанализируем предъявляемые ими требования к ресурсам времени и пространства.

Примеры, которые рассматривались до сих пор, могут создать ложное впечатле­ние, что рассматриваемые программы поиска могут применяться только в простран­ствах состояний, которые представляют собой деревья, а не графы в любой форме. Но при поиске в графе он, по сути, развертывается в дерево таким образом, чтоне­которые пути, возможно, копируются в другие части дерева. Такая ситуация иллю­стрируется на рис. 11.8. Поэтому рассматриваемые программы работают также с графами, но могут без какой-либо необходимости продублировать часть работы в тех случаях, если некоторый узел можетбыть достигнут разными путями. Такое разви­тие событий можно предотвратить, проверяя, не произошло ли повторное появление некоторого узла во всех возможных путях, а не только в том пути, в котором был сформирован этот узел. Безусловно, что такая проверка возможна в рассматриваемых программах поиска в ширину только в тех случаях, если для проверки доступны альтернативные пути.

Часть II. Применение языка Prolog в области искусственного интеллекта

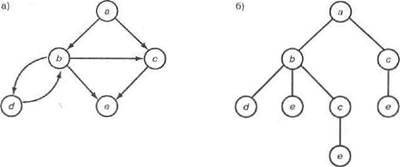Рас. 11.8. Пример дублирования узлов: а) пространства состояний, в котором а представляет собой начальный узел; б) дерево всех возмож­ных ациклических путей из узла з, которое, по сути, формируется про граммой поиска в ширину, приведенной в листинге 11.3

Рассматриваемые программы поиска в ширину вырабатывают один за другим пу­ти решений, упорядоченные по длине, причем вначале формируются кратчайшие решения. Это важно, если необходимо обеспечить получение оптимальных решений (с точки зрения длины). Стратегия поиска в ширину гарантирует первоочередную выработку кратчайших решений. Это утверждение, безусловно, не относится к стра­тегии поиска в глубину. Но во время поиска в глубину с итеративным углублением такой поиск выполняется с постепенно увеличивающимися пределами глубины, и поэтому наблюдается тенденция к тому, что в первую очередь обнаруживаются крат­чайшие решения. Таким образом, при итеративном углублении происходит своего рода моделирование поиска в ширину.

Но в приведенных в данной главе программах не учитываются какие-либо стои­мости, связанные с дугами в пространстве состояний. Если в качестве критерия оп­тимизации рассматривается минимальная стоимость пути решения (а не его длина), поиск в ширину не может обеспечить выбор оптимального пути решения. Для опти­мизации стоимости предназначен поиск по заданному критерию, который рассмат­ривается в главе 12.

Типичной проблемой, связанной с поиском, является комбинаторная сложность. При наличии нетривиальных проблемных областей количество вариантов, подлежа­щих рассмотрению, становится столь значительным, что наибольшее значение при­обретает существенное увеличение затрат ресурсов на исследование данных вариан­тов. Можно легко проанализировать причины того, почему это происходит. Для уп­рощения такого анализа предположим, что пространство состояний представляет собой дерево с единообразным ветвлением Ь. Это означает, что каждый узел в дереве, за исключением листьев, имеет точно b преемников. Предположим, что кратчайший путь решения имеет длину d, и в дереве на глубине d или меньшей отсутствуют ли­стья. Количество альтернативных путей длины d от начального узла равно ъ°. При поиске в ширину количество рассматриваемых путей пропорционально Ь". Это обо­значается как О (Ь^с) . Итак, количество возможных путей очень быстро возрастает при увеличении их длины, что приводит к так называемому комбинаторному взрыву.

Теперь сравним затраты ресурсов на осуществление основных алгоритмов поиска. Потребность в ресурсах времени обычно определяется в зависимости от количества узлов, формируемых алгоритмом поиска, а затраты ресурсов пространства обычно определяются в зависимости от максимального количества узлов, которые должны храниться в памяти во время поиска.

Рассмотрим поиск в ширину в дереве с коэффициентом ветвления Ь и кратчай­шим путем решений длиной d. Количество узлов на последовательно углубляющихся

Глава 11.Основные стратегии решения проблем

уровнях дерева возрастает экспоненциально с глубиной, поэтому количество узлов, вырабатываемых при поиске в ширину, можно определить следующим образом:

1 + b ■to² + b 3 + . . .

Общее количество узлов, вплоть до глубины решения с, составляет Э(Ь^П), поэто­му затраты ресурсов времени при поиске в ширину измеряются значением Qjb^). Кроме того, при поиске в ширину информация обо всех возможных путях хранится в памяти, поэтому затраты ресурсов пространства также измеряются значением 0(b^d).

Задача анализа неограниченного поиска в глубину является менее очевидной, по­скольку при таком поиске система может полностью пропустить правильный путь решения длиной о и неограниченно долго продолжать поиск в бесконечном поддере­ве. Для упрощения анализа рассмотрим поиск в глубину, ограниченный максималь­ной глубиной d_raaK, такой, что d < cW Затраты времени при этом измеряются зна­чением ОоЛынс). Но затраты ресурсов пространства составляют всего C(d_ms*). При

поиске в глубину, по сути, сопровождается лишь путь между начальным и текущим узлами поиска, рассматриваемый Б настоящее время. Преимущество поиска в глуби­ну по сравнению с поиском в ширину состоит в том, что он требует намного меньших затрат ресурсов пространства, а его недостатком является то, что он не гарантирует получение оптимального решения.

При итеративном углублении выполняется поиск в глубину (d + 1) со все воз­растающей глубиной: О, I, ..., d. Поэтому затраты ресурсов пространства при этом по­иске измеряются значением 0!d). Посещение начального узла происходит {d + 1) раз, дочерних узлов начального узла — d раз и т.д. В худшем случае количество формируемых узлов измеряется следующим выражением: (d+l)*l + d*b + (d-l}*b² + ... + l*b^d

Это выражение также измеряется значением 0(b^d;. Но фактически затраты на повторное формирование узлов верхних уровней по сравнению с поиском в ширину весьма малы. Можно показать, что отношение между количеством узлов, вырабаты­ваемых при итеративном углублении и при поиске в ширину, составляет приблизи­тельно Ь/ ! b - 1) . При Ь Ь 2 такие дополнительные расходы на итеративное углуб­ление относительно невелики, если к тому же учесть весьма значительное уменьше­ние потребности в пространстве по сравнению с поиском в ширину. В этом смысле итеративное углубление сочетает в себе наилучшие свойства поиска в ширину (гарантированное достижение оптимального решения) и поиска в глубину (экономия пространства) и поэтому на практике часто является наиболее предпочтительным среди всех основных методов поиска.

Рассмотрим также двунаправленный поиск (упражнения 11.10-11.12). В тех слу­чаях, если этот метод поиска является применимым (известен целевой узел), он мо­жет привести к значительной экономии. Предположим, что имеется граф поиска с единообразным ветвлением b в обоих направлениях, а двунаправленный поиск реа­лизован как поиск в ширину в обоих направлениях. Допустим, что кратчайший путь решения имеет длину d, поэтому двунаправленный поиск окончится, когда встретят­ся оба пути поиска в ширину; это означает, что оба эти пути пройдут приблизитель­но до середины между начальным и целевым узлами. Таким образом, встреча путей произойдет, когда они пройдут от своих соответствующих узлов на глубину, состав­ляющую примерно d/2. Поэтому затраты ресурсов при выполнении поиска в каждом из направлений измеряются значением, которое ориентировочно равно Ь . При та­ких благоприятных обстоятельствах двунаправленный поиск позволяет найти путь решения длиной d с потреблением примерно таких же ресурсов, как при поиске в ширину, но в результате решения более простой задачи с длиной пути решения, рав­ной d/2. В табл. 11.1 приведены итоговые данные, позволяющие провести сравнение основных методов поиска.

244 Часть II. Применение языка Prolog в области искусственного интеллекта

Таблица 11.1. Приближенные оценки затрат ресурсов, связанных с использованием основных методов поиска. Здесь b - коэффициент ветвления, d - длина кратчайшего пути решения, d™, предел глубины при поиске в глубину, d_< dr.«

Метод поиска Время Пространство Сам ое к оротк: ое га р а нтир уе мое решен и

е

Поиск в ширину		Ъ"	b	да
Поиск а глубину		b<W	■drrai	l-.Cl
Итеративное углубление		ъ"	d	да
Двунаправленный, если он	возможен	bd/2	ьа/3	да

Рассматриваемые в данной главе основные методы поиска не обеспечивают вы­полнения каких-либо обоснованных действий, позволяющих преодолеть комбинатор­ный взрыв. В них все возможные пути рассматриваются как в равной степени пер­спективные и не используется какая-либо информация, относящаяся к конкретной задаче, для управления ведением этого поиска в более перспективном направлении. В данном смысле эти методы не являются достаточно информационно насыщенными. Поэтому описанные в этой главе простые методы поиска не позволяют решать круп­номасштабные задачи. При решении подобных задач необходимо использовать ин­формацию, относящуюся к конкретной проблеме, для обеспечения целенаправленно­го поиска. Такая руководящая информация называется эвристикой. Алгоритмы, в которых применяются эвристики, обеспечивают выполнение эвристического поиска. Подобный метод поиска представлен в следующей главе.

Резюме

•

Пространство состояний используется в качестве формализованной структу­ры для представления проблем.

Пространство состояний - это ориентированный граф, узлы которого соответ­ствуют проблемным ситуациям, а дуги •— возможным действиям. Конкретная задача определяется с помощью начального узла и целевого состояния. В та­ком случае решение задачи соответствует одному из путей в графе. Поэтому решение задачи сводится к поиску пути в графе.

Задачи оптимизации можно моделировать, назначая стоимости дугам в про­странстве состояний.

Тремя основными стратегиями поиска, которые позволяют систематически ис­следовать пространство состояний, являются поиск в глубину, поиск а ширину и итеративное углубление.

Разработка программы поиска в глубину может быть осуществлена проще все­го, но такая программа восприимчива к образованию циклов. Для предотвра­щения циклов применяются два простых метода: ограничение глубины поиска и проверка на наличие повторяющихся узлов.

Реализация стратегии поиска в ширину сложнее, поскольку требует сопровож­дения множества возможных путей. Проще всего такое множество можно представить как список списков.

Поиск в ширину всегда позволяет в первую очередь найти кратчайший путь решения, но это утверждение не относится к стратегии поиска в глубину.

Для поиска в ширину требуется больше пространства, чем для поиска в глу­бину. На практике пространство часто является наиболее важным и ограни­ченным ресурсом.

Метод поиска в глубину с итеративным углублением сочетает в себе наилуч­шие свойства поиска в глубину и в ширину.

Глава 11 .Основные стратегии решения проблем

• В случае больших пространств состояний возникает опасность комбинаторного взрыва. Простые стратегии поиска плохо подходят для преодоления возни­кающих при этом сложностей. Поэтому в подобных случаях необходимо руко­водствоваться эвристическими методами.

• В настоящей главе представлены следующие понятия;

• пространство состояний;

• начальный узел, целевое условие, путь решения;

• стратегия поиска;

• поиск в глубину;

• поиски ширину;

• поиск с итеративным углублением;

• двунаправленный поиск;

• эвристический поиск.