Проблема разделения в самообучаемых экспертных системах

Допустим, мы имеем N категорий объектов, описанных замерами на определенном наборе переменных. Затем предъявляется еще один объект, заданный совокупностью М замеров на том же наборе переменных. Сле­дует определить, к какой из N категорий принадлежит объект.

Если сформулировать эту проблему применительно к задаче техни­ческого диагностирования состояния АСУ ТП, то проблема будет выгля­деть следующим образом. В системе АСУ ТП имеются датчики, исполни­тельные механизмы, управляющие узлы и т.д.

Для каждого отдельно взятого узла АСУ ТП определены: замеры па­раметров системы (напряжение, расход, давление, температура, влажность и т.д.), при которых этот узел находится в категории S₁ (например, полно­стью исправен); замеры параметров системы, при которых этот узел нахо­дится в категории S₂ (например, для датчика погрешность превышает оп­тимальную, но остается допустимой); ... ; замеры параметров системы, при которых этот узел находится в категории S_N (полной неработоспособно­сти).

Требуется по замеру параметров системы в произвольный момент времени определить, в какую из N категорий попадает данный узел сис­темы.

Если N = 2, то требуется просто определить, исправен данный узел или неисправен.

Вообще говоря, поставленная проблема решается только в том слу­чае, если указанные категории линейно сепарабельны. Это значит, что ме­жду каждой из категорий можно поместить разделяющую поверхность или ряд поверхностей. Поверхность определяется в терминах, которые легко измерить для данных объектов.

Если категории являются взаимоисключаемыми, т.е. объект в со­стоянии попасть только в одну из них (например, исправен – неисправен), то объект по результатам замеров помещают в наиболее вероятную кате­горию. Другими словами, помещают его в такую категорию, для которой значение вероятности р (Н: E) максимально. Здесь гипотеза Н соответст­вует одной из N категорий, а событие Е – все замеры, которые позволяют отнести объект к этой категории.

Заметим, что математически р (Н: E) является уравнением поверхно­сти, которое в общем виде выглядит следующим образом:

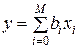, (4.7)

где b_i – константы; x_i – переменные. Это та поверхность, которая «указы­вает» в направлении конкретной гипотезы Н.

Проблему разделения можно решать двумя способами. Если x_i – пе­ременная, которая определяет текущее состояние системы – является дис­кретной и принимает значение 0 и 1 («да» или «нет»), то можно воспользо­ваться системой, принимающей решения по максимальной вероятности. Если x_i является непрерывной величиной, то можно воспользоваться сис­темой, принимающей решения по наименьшему расстоянию.