Лабораторная работа №9. Аффинные преобразования в пространстве

Цель работы: Закрепить лекционный материал по изучению материала одноименной темы, реализовав матрицы переноса, масштабирования, отражения и вращения применительно к координатам описанной в программе объемной фигуры (многогранника) с целью демонстрации движения и преобразования формы этой фигуры в пространстве.

Краткие теоретические сведения.

Пусть дана тройка векторов a,b,c с общим началом в точке О (начале координат), не лежащих в одной плоскости. Относительно точки О положение любой точки M в пространстве характеризуется ее радиус - вектором r. Если принять векторы a,b,c за базис и представить r=l*a+w*b+v*c, то положение точки М характеризуется набором чисел (l,w,v), называемых аффинными координатами точки М, т.е.координатами ее радиус-вектора r. Если базис (a,b,c) - единичный и взаимно перпендикулярный, то система координат - декартова. Тогда основные векторы (a,b,c) принято обозначать как i,j,k- декартов базис, координаты - (x,y,z), r=x*i+y*j+z*k.

Как и на плоскости следует применять геометрические преобразования к точкам изображения. Точка в пространстве задается либо радиус-вектором r; либо матрицами координат (x y z). Аффинные преобразования пространства определяются системой координат Oxyz, матрицей коэффициентов: и числами m,n,l ,осуществляющими перенос изображения.

Если новая и старая системы координат имеют одно начало, преобразования в матричной форме выглядят так:

В противном случае целесообразно прибегнуть к однородным координатам:

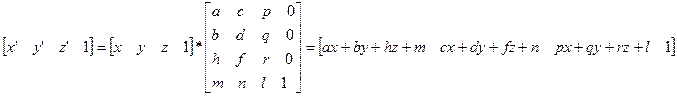
Направляющие косинусы вектора - это косинусы углов, которые он образует с осями координат. Они полностью определяют направление вектора. Если вектор а=a_x*i+a_y*j+a_z*k, то a_x -проекция вектора a на ось x, умноженная на косинус угла между векторами и осью x. Аналогично для a_y и a_z. Если вектор а задан координатами начальной и конечной точек (x1,y1) и (x2,y2), направляющие косинусы определяются уравнениями:

где α,β,γ - углы, которые вектор а образует с осями Ох, Оy, Oz, соответственно.

Частные случаи аффинных преобразований:

1.Сдвиг - перенос точки (x,y,z) на m единиц по координате x, на n - по y, на l единиц- по z.: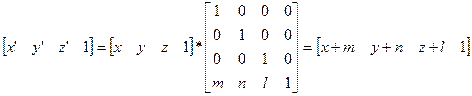

2.Повоpот точки (x,y,z) вокpуг оси абсцисс на угол δ: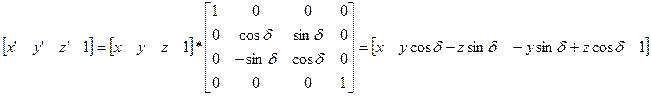

вокруг оси ординат на угол λ:

вокруг оси аппликат на угол μ:

вокруг оси, проходящей через начало координат на угол ν

.

Здесь n₁,n₂,n₃ - направляющие косинусы вращения. Если ось вращения проходит через начало координат и точку (x₁,y₁, z₁) то

Вращение вокруг произвольной оси осуществляется переносом ее вместе с изображением в начало координат, вращением вокруг перенесенной оси и обратным переносом изображения в исходное положение. Итоговая матрица будет определена умножением соответствующих простых матриц.

3. Симметрия относительно координатных плоскостей осуществляет зеркальное отображение 3D-изображения.

Относительно плоскости XOY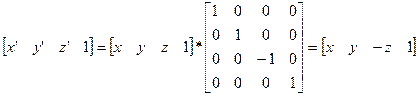

Плоскости XOZ - -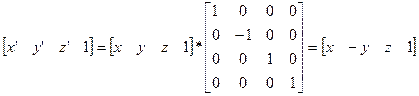

Плоскости YOZ : -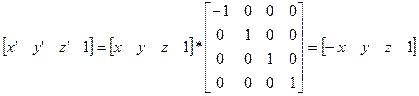

Симметрия относительно произвольной плоскости - это сложное преобразование, осуществляемое из простых поэтапно:

· совмещение плоскости симметрии с одной из координатных

· отражение относительно этой координатной плоскости

· обратное преобразование, возвращающее плоскость симметрии в исходное состояние.

4.Масштабирование осуществляется диагональными элементами матрицы преобразования.

Относительно начала координат: ,

где k_x, k_y, k_z - коэффициенты искажения вдоль осей ox,oy,oz, соответственно.

Относительно произвольного центра с координатами (m,n,l):

-

Любое другое преобразование может быть представлено суперпозицией вращений, переносов, отражений, растяжений (сжатий).

Задание на лабораторную работу:

Написать на языке PASCAL программу:

1. Описывающую многогранник (куб) в приборной системе координат.

2. Смещающую его на n пикселов вправо, m - вниз, p - вглубь.

3. Зеркально отражающую относительно плоскостей координат.

4. Растягивающую (сжимающую) его вдоль координатных осей относительно некоторой заданной точки.

5. Вращающую его относительно линии, проходящей через начало координат (относительно координатных осей, диагонали многогранника).

Для показа результатов работы пунктов 2-4 можно воспользоваться аксонометрической проекцией многогранника (любой по выбору), для пункта 5 задания можно использовать ортогональную проекцию.

Дополнительное задание:

1.Реализовать сложное преобразование, например, вращение с уменьшением.

2.Задание выполнить с помощью программ работы с мышью.

Требования к защите лабораторной работы

Защита работы состоит из демонстрации преподавателю результатов выполнения заданий на лабораторной работе и ответов на задаваемые преподавателем вопросы по ходу демонстрации.

Требования к отчету

Отчет выполняется на отдельных листах формата А4. Содержит титульный лист с названием работы, оформленный согласно требованиям кафедры и распечатку программы - результат выполнения заданий лабораторной работы с обязательными комментариями.

Вопросы для самоподготовки:

1. Для чего используются однородные координаты?

2. Какие преобразования считаются простыми, как выглядят матрицы таких преобразований?

3. Что такое направляющие косинусы вращения, как они определяются и где используются?

4. Каков смысл у знаков "минус" в матрицах вращения?

5. Каким образом значения коэффициентов масштабирования влияют на изображение?

6. Как осуществить любое сложное преобразование?

Литература:

1. Фоли, Дж. Основы интерактивной машинной графики [текст]: В 2 кн. кн. 1 / Дж. Фоли, А. Дэм; под ред. Ю. М. Баяковского; пер. с англ. В. А. Галактионова и др. - М.: Мир, 1985. - 367c.: ил.

2. Гилой, В. К. Интерактивная машинная графика: Структуры данных, алгоритмы, языки [текст] / В. К. Гилой; пер. с англ. под ред. Ю. М. Баяковского. - М.: Мир, 1981. - 380c.: ил.

3. Шикин, Е. В. Компьютерная графика: Динамика, реалист. изображения [текст] / Е. В. Шикин, А. В. Боресков. - М.: ДИАЛОГ-МИФИ, 1996. - 287c.: ил.

4. Боресков, А. В. Компьютерная графика: первое знакомство [текст] / А. В. Боресков, Е. В. Шикин, Г. Е. Шикина; Под ред. Е. В. Шикина. - М.: Финансы и статистика, 1996. - 176c.: ил. - (Диалог с компьютером).