Регулярный подграф степени d
Подграф называется регулярным подграфом степени 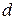 , если степень каждой его вершины равна
, если степень каждой его вершины равна 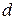 .
.
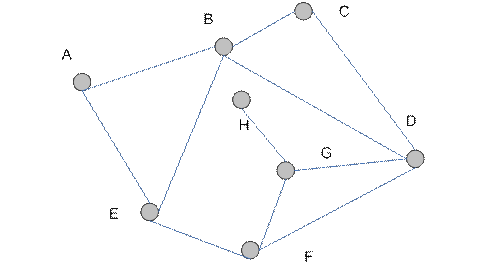
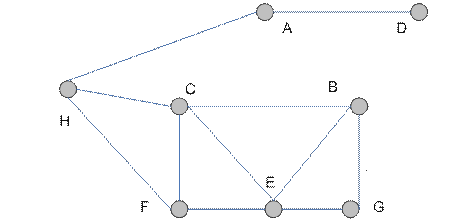
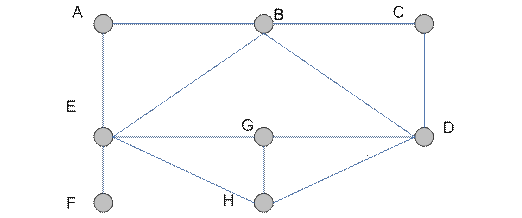
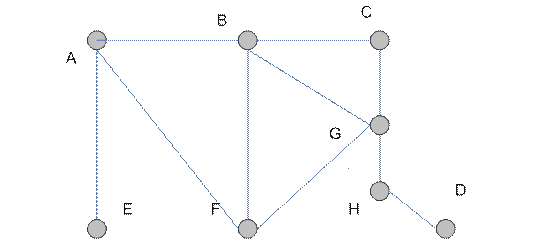
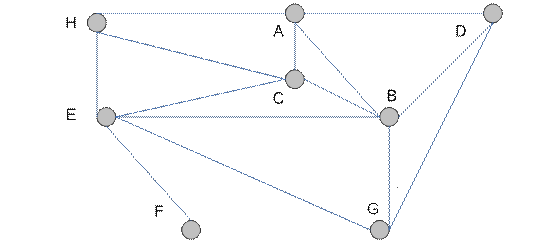
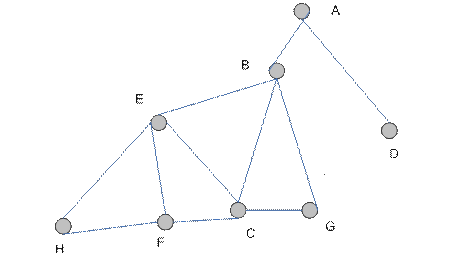
Например, граф (рис. 4.6) имеет регулярный подграф 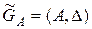 степени 3, где
степени 3, где 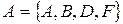 .
.
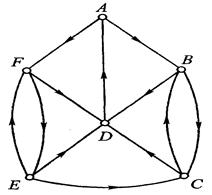
Рис. 4.6
Понятия гамильтонова цепь и гамильтонов цикл определяются аналогично существующим понятиям для путей и контуров, только вместо дуг рассматриваются ребра, а понятия подграфа и частичного графа – аналогично существующим понятиям для ориентированных графов.
Хроматическое число
Понятие хроматического числа относится к неориентированным графам.
Граф называют 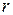 -хроматическим, если его вершины можно раскрасить
-хроматическим, если его вершины можно раскрасить 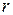 различными цветами так, что никакие смежные вершины не окрашены одинаково.
различными цветами так, что никакие смежные вершины не окрашены одинаково.
Наименьшее число 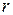 , для которого граф является
, для которого граф является 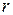 -хромати-ческим, называется хроматическим числом неориентированного графа и обозначается через
-хромати-ческим, называется хроматическим числом неориентированного графа и обозначается через 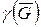 .
.
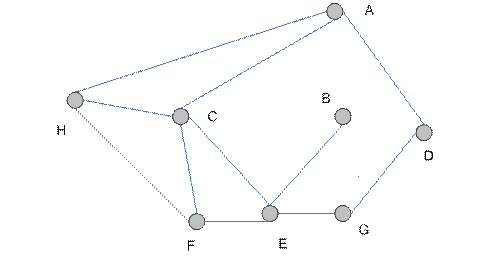
Например, на схеме-карте (рис. 4.7) изображены 10 районов.
Эту схему можно раскрасить четырьмя цветами: голубым Г, желтым Ж, зеленым З и красным К так, что никакие два соседних района не будут окрашены одинаково.
Можно проверить, что с меньшим числом цветов этого сделать невозможно.
Вершины, окрашенные одинаково, образуют внутренне устойчивое множество, и хроматическое число можно определить как минимальное число внутренне устойчивых множеств, которые покрывают в совокупности все вершины графа.
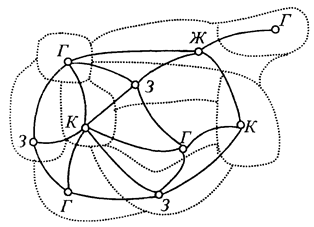
Рис. 4.7
Нахождение 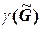
Воспользуемся методом Магу. Напомним формулу нахождения семейства минимально внутренне устойчивых подмножеств
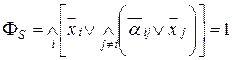 , (4.5)
, (4.5)
по которой находятся все внутренне устойчивые подмножества.
Принимая во внимание соотношение 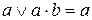 , запишем выражение (4.5) как
, запишем выражение (4.5) как
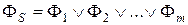 , (4.6)
, (4.6)
где 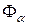 - одночлен от переменных с отрицанием.
- одночлен от переменных с отрицанием.
Возьмем вершину 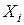 и член
и член 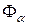 , не содержащий
, не содержащий 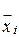 , т.е. определяющий максимально внутренне устойчивое множество, которое содержит
, т.е. определяющий максимально внутренне устойчивое множество, которое содержит 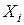 .
.
Введем булевы переменные 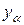 , каждая из которых принимает значение 1 в точности на одном подмножестве (соответствующем
, каждая из которых принимает значение 1 в точности на одном подмножестве (соответствующем 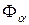 ), таком, что его вершины предполагается раскрасить одинаково, и 0 - в остальных случаях. Тогда для окраски
), таком, что его вершины предполагается раскрасить одинаково, и 0 - в остальных случаях. Тогда для окраски 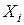 необходимо, чтобы
необходимо, чтобы
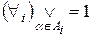 , (4.7)
, (4.7)
где 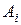 - множество таких индексов
- множество таких индексов 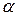 , что
, что 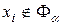 .
.
Следовательно, для этого способа окраски графа необходимо и достаточно, чтобы
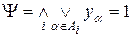 . (4.8)
. (4.8)
Обозначим через 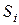 максимальное внутренне устойчивое множество, соответствующее
максимальное внутренне устойчивое множество, соответствующее 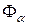 .
.
Тогда одночлен
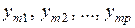 (4.9)
(4.9)
в разложении (4.5) указывает следующий способ окраски графа 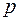 цветами:
цветами: 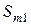 окрашиваем цветом 1,
окрашиваем цветом 1, 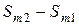 - цветом 2,
- цветом 2, 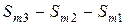 - цветом 3 и т.д.
- цветом 3 и т.д.
Если представить (4.8) в виде дизъюнкции
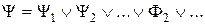 , (4.10)
, (4.10)
то хроматическое число графа 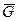
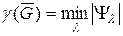 . (4.11)
. (4.11)
Пример
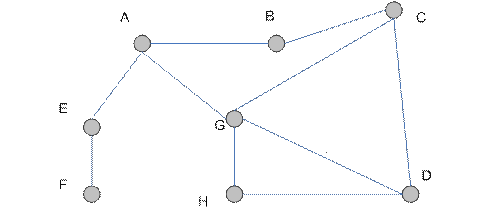
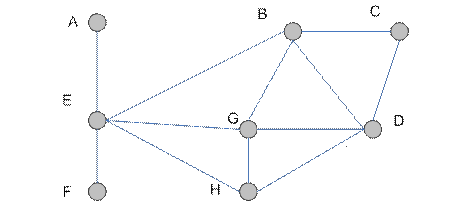
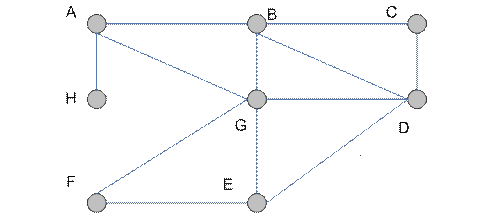
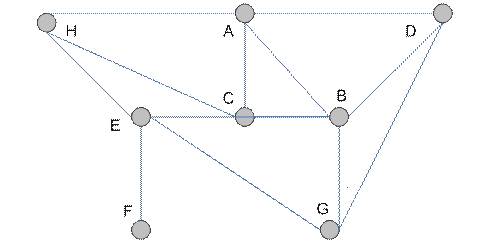
Рассмотрим неориентированный граф 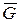 на рис 4.8 и определим его
на рис 4.8 и определим его 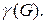
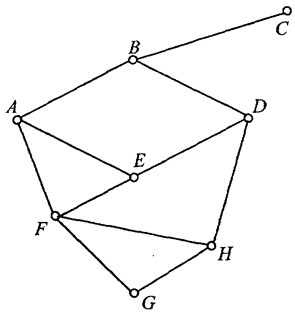
Рис. 4.8
Решение
Воспользуемся определенной в подразделе. 2.4.2 (см. методичку по теории гафов) формулой
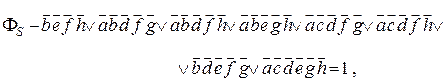 (4.12)
(4.12)
или
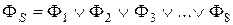 . (4.13)
. (4.13)
Так как 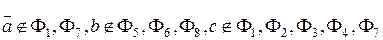 и т. д., то
и т. д., то
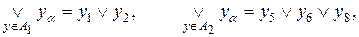
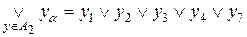 и т.д.
и т.д.
Согласно (4.8)
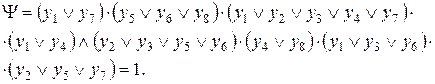 (4.14)
(4.14)
После упрощения
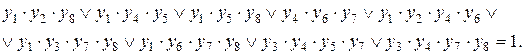
Запишем (4.14) в виде (4.13):
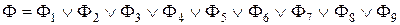 .
.
Тогда очевидно, что
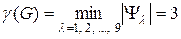 . (4.5)
. (4.5)
Таким образом, граф можно раскрасить тремя цветами: К, З и Ж в соответствии с
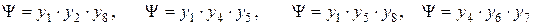 .
.
Из выражения (4.12) получаем
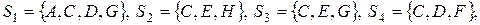
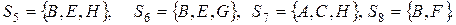
В результате получим, что 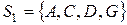 окрашивается в К цвет,
окрашивается в К цвет, 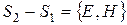 - в З цвет,
- в З цвет, 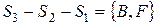 - в Ж цвет.
- в Ж цвет.
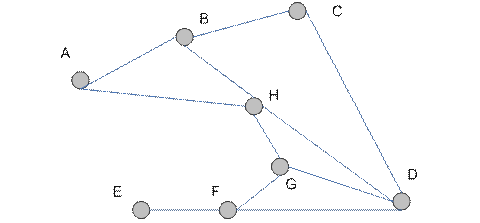
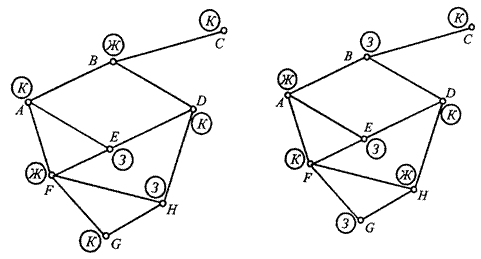
На рис. 4.9 изображены всевозможные способы раскраски графа тремя цветами.
Приведем без доказательства следующие теоремы о хроматическом числе графа (доказательства можно найти в [2, 7]).
Теорема 1 (Кенига)
Граф является двухроматическим тогда и только тогда, когда он не содержит циклов нечетной длины.
Теорема 2
Для того, чтобы граф 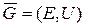 был
был 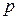 -хроматическим, необходимо и достаточно, чтобы существовал соответствующий ему симметрический граф
-хроматическим, необходимо и достаточно, чтобы существовал соответствующий ему симметрический граф 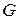 без петель, допускающий такую функцию Гранди
без петель, допускающий такую функцию Гранди 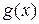 , что
, что
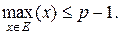
 |
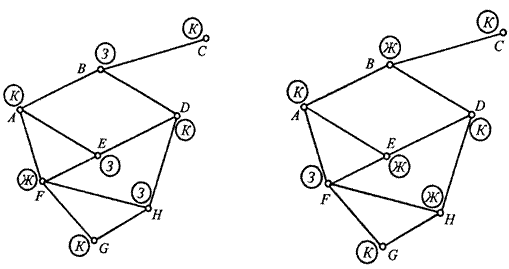 |
Рис. 4.9
Согласно теореме 2 отыскание функции Гранди для симметрического графа без петель сводится к задаче о раскраске соответствующего неориентированного графа. Любой раскраске отвечает функция Гранди и, наоборот, любой функции Гранди отвечает некоторая раскраска графа.
Рассмотрим в качестве примера симметрический граф без петель (рис. 4.10), соответствующий неориентированному графу, изображенному на рис. 4.8, исходя из раскраски, заданной  (см. рис. 4.9), получаем функцию Гранди с соответствием
(см. рис. 4.9), получаем функцию Гранди с соответствием 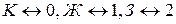 .
.
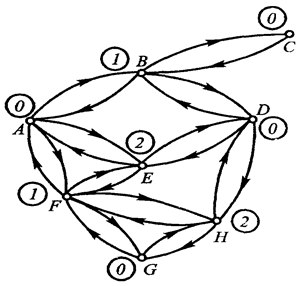 |
Рис. 4.10
Хроматический класс
Пусть граф 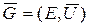 и
и 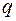 - целое число, такое, что:
- целое число, такое, что:
1) ребра графа можно раскрасить 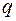 цветами так, чтобы смежные ребра не окрашивались одинаково;
цветами так, чтобы смежные ребра не окрашивались одинаково;
2) окраска ребер невозможна 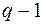 цветами.
цветами.
Число 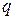 называется хроматическим классом графа
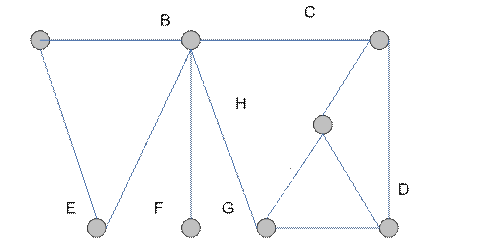
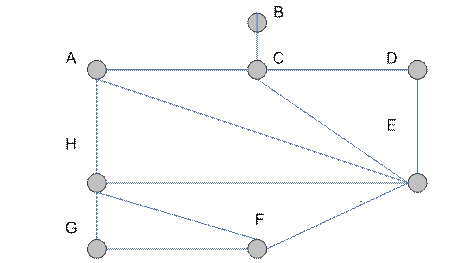
называется хроматическим классом графа 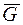 . Например, хроматический класс графа, изображенного на рис. 4.11, равен пяти, так как необходимо пять цветов для требуемой окраски. Вычисление
. Например, хроматический класс графа, изображенного на рис. 4.11, равен пяти, так как необходимо пять цветов для требуемой окраски. Вычисление 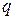 для
для 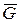 сводится к задаче нахождения хроматического числа графа
сводится к задаче нахождения хроматического числа графа 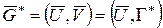 , вершинами которого служат ребра
, вершинами которого служат ребра
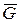 и
и 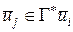 , если
, если 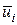 и
и 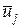 - смежные ребра в
- смежные ребра в 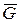 .
.
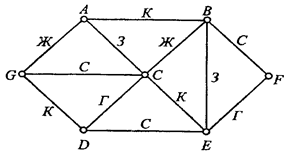 |
Рис. 4.11
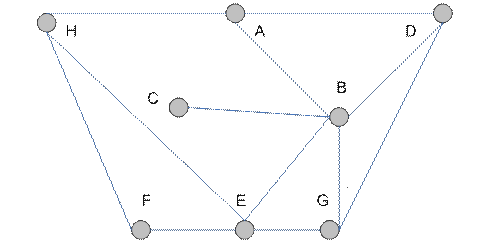
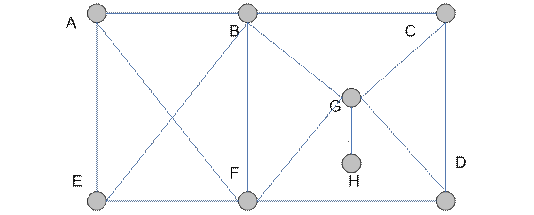
На рис. 4.12 показано, как получить 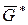 (изображен пунктиром) из
(изображен пунктиром) из 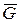 и раскраску всех ребер
и раскраску всех ребер 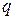 цветами.
цветами.
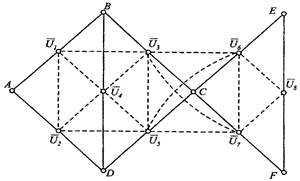 |
Рис. 4.12
Задачи
1 Ознакомиться с приведенными теоретическими понятиями о неориентированных графах.
2 Изучить понятия хроматического числа и хроматического класса, а также способы их нахождения с помощью приведенных примеров.
3 Решить вручную задачу нахождения хроматического числа и хроматического класса для графа своего варианта. Найти все возможные варианты раскраски графа.
4 Написать программу (в произвольно выбранной среде программирования), которая реализует поиск хроматического числа, хроматического класса и способов раскраски графа.
Содержание отчета
1 Постановка задачи для своего варианта.
2 Ручные вычисления поставленной задачи для графа своего варианта с промежуточными вычислениями, указать найденные хроматическое число, хроматический класс и варианты раскраски графа. Для упрощения оформления отчета рекомендуется представить в рукописном виде.
3 Описание программной реализации: объектов, процедур, функций с указанием параметров и их смыслового содержания.
4 Листинг программы. Наличие комментариев в листинге обязательно.
5 Результат работы программы для графа своего варианта.
6 Выводы.
Варианты
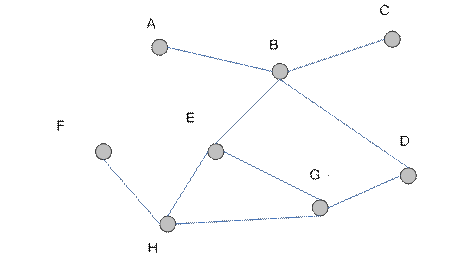
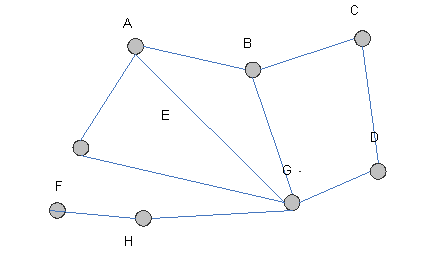
5