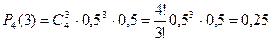Формула Бернулли

Предположим, что несколько одинаковых машин в одних и тех же условиях перевозят груз. При этом любая машина может выйти из строя, Пусть вероятность выхода из строя одной машины не зависит от выхода из строя других машин. Это значит, что рассматриваются независимые события (испытания). Вероятности выхода из строя каждой из этих машин примем одинаковыми (р).

Пусть в общем случае проводится n независимых испытаний. Задача такова: определить вероятность того, что в т испытаниях наступит событие А, если вероятность его наступления в каждом испытании равна р. В нашем примере это может быть вероятность выхода из строя одной машины, двух машин и т. д.

Определим вначале вероятность того, что в первых т испытаниях событие А наступит, а в остальных n-т испытаниях не наступит. Вероятность такого события можно получить по формуле вероятности про- изведения независимых событий

где q=1-p

Заметим, что это лишь одна из возможных комбинаций, когда событие А произошло только в первых m испытаниях. Для определения искомой вероятности нужно перебрать все возможные комбинации. Их число равно числу сочетаний из n элементов по m, т.е.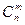

Таким образом, вероятность появления ровно m раз события А в серии из n независимых испытаний, в каждом из которых вероятность появления события А равна р определяется по формуле:

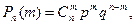(3)

где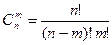

Формула (3) называется формулой Бернулли.

Пример. В четырех попытках разыгрываются некоторые предметы. Вероятность выигрыша в каждой попытке равна 0,5. Какова вероятность выигрыша трех предметов?

РЕШЕНИЕ. По формуле Бернулли находим