Построение тестов

Построение тестов является обратной задачей диагноза. Напомним ее постановку [1]. Определить подмножество элементарных проверок T_ij, различающих заданную пару неисправностей (F_i, F_j) объекта диагноза (ОД). Решение этой задачи для всех возможных пар неисправностей дает тест поиска места дефекта. Обратная задача относится к классу NP-полных или трудноразрешимых задач, решение которых может быть получено только полным перебором. Поэтому на практике ограничиваются случаем, когда одним из элементов пары является исправное устройство. В такой постановке результатом является проверяющий тест.

Пусть f(x) – функция, реализуемая исправным ОД, а f ¢(x) – неис­правным. Тогда решение логического уравнения f(x) mod2 f ¢(x) = 1 будет решением обратной задачи диагноза. f ¢(x) находится из диагностической модели ОД.

В практическом построении тестов используется структурная логи­ческая модель ОД, когда заданы элементы и связи между ними. Нахожде­ние элементарных проверок по структурной модели базируется на понятии существенного пути, лежащего в основе организации перебора вариантов решения.

Пусть в объекте диагноза имеется некоторый дефект. Из очевидных соображений следует, что одиночный дефект может быть обнаружен эле­ментарным тестом, обладающим следующими свойствами.

Первое свойство состоит в том, что возникшая неисправность прояв­ляется, т.е. вызывает появление значения хотя бы одного внутреннего сиг­нала ОД, отличного от значения, которое этот сигнал имел бы в исправном состоянии. Это свойство называют условием проявления неисправности.

Второе свойство формулируется следующим образом. Значения сиг­налов, вызванные проявлением неисправности, передаются на один или несколько выходов ОД так, чтобы они отличались для исправного и неис­правного случаев. Это означает образование существенного (активизиро­ванного) пути распространения эффекта неисправности в ОД.

Рассмотрим фрагмент логической схемы (рис. 4.7). Неисправность С0 на входе d элемента ИЛИ может быть обнаружена на его выходе набо­ром (d = 1, e = 0, f = 0). Этот входной набор также обнаруживает неисправ­ность c = С0. Запись значения сигнала в виде 1/0 (0/1) означает 1(0) в ис­правном случае и 0(1) в неисправном случае.

Нельзя непосредственно наблюдать значение сигнала во внутренней точке с, поэтому необходимо задать входы элемента И так, чтобы наблю­дать эффект неисправности на его выходе, т.е. (a = 1, b = 1). При этих зна­чениях изменение сигнала на входе с приводит к изменению сигнала на выходе g. В этом примере d – c – g – существенный (активизированный) путь, значения сигналов на d, e и f – условия проявления неисправности, а на b и a – условия активизации.

4.2.1. Построение тестового набора методом активизации существенного пути

Идея этого метода заключается в выборе пути от места неисправно­сти, скажем от элемента А (неисправность Сх) через последовательность элементов B, C, … , Z к некоторому выходу схемы y (рис. 4.8). Пути в схеме могут быть как одномерные, так и многомерные, т.е. проходящие через разветвления сразу в нескольких направлениях.

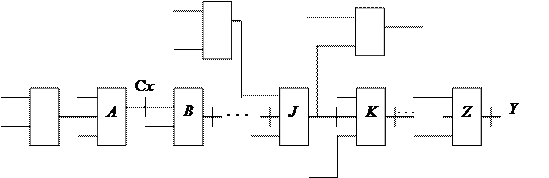
Рис. 4.8. Выбор пути

Значения непомеченных входов элементов B, C, …, Z выбираются по второму свойству так, что значения выходов элементов определяются только значениями помеченных входов, а о значении выхода элемента A можно сделать вывод, наблюдая выход z элемента Z. Значения входов эле­мента A должны быть заданы так, чтобы о наличии или отсутствии неис­правности можно было бы судить по значению сигнала на его выходе. Эти действия называют прямой фазой активизации существенного пути или просто активизацией. Необходимо далее так установить внешние входы, чтобы обеспечить требуемые значения на входах элементов А, B, C, …, Z. Для этого прослеживаются назад пути по схеме от входов элементов А, B, C, …, Z до внешних входов схемы и выбираются соответствующие значения сигналов на входах задействованных элементов. Эти действия называют об­ратной фазой активизации существенного пути, или доопределением.

Как прямая, так и обратная фазы связаны с перебором вариантов. Выбор очередного варианта происходит при возникновении противоречия в момент присвоения значений линиям схемы. Задача сокращения пере­бора решается путем как можно более раннего обнаружения противоречия. Это приводит к уменьшению прохождения числа путей в дереве решений.