Занятие 2. Пользовательские функции

Ранее в программах мы использовали функции из разных библиотек, например, sin(x) из библиотеки <math.h> или setw(10) из библиотеки <iomanip>. Что общего во всех функциях? Все функции представляют собой некий шаблон, по которому вычисляется значение какой-то функции или выполняется набор каких-то действий. В языке С++ есть возможность создавать свои функции, не относящиеся к библиотекам. Такие функции называются пользовательскими функциями.

Для того, чтобы создать и использовать свою пользовательскую функцию в программе, необходимо:

1. объявить пользовательскую функцию:

тип_данных имя_функции (список параметров);

здесь тип_данных – это возвращаемый тип данных функции, который определяется ответом функции (выходные данные), имя функции – любое имя (по аналогии с именем переменной), список параметров – это то, с чем наша функция будет работать (входные данные);

2. описать пользовательскую функцию;

3. вызвать пользовательскую функцию.

Объявление пользовательской фукнции должно быть обязательно до функции main(), описание может быть вместе с объявлением, а может быть после функции main(). Вызов пользовательской функции может быть внутри функции main() или внутри другой пользовательской функции.

Первый вариант описания пользовательской функции – до функции main() представлен на рис. 4.

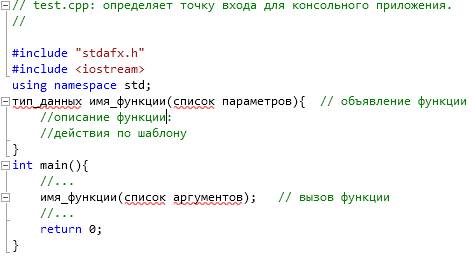
Рис. 4 Описание пользовательской функции до функции main()

Второй вариант описания пользовательской функции – после функции main() представлен на рис. 5.

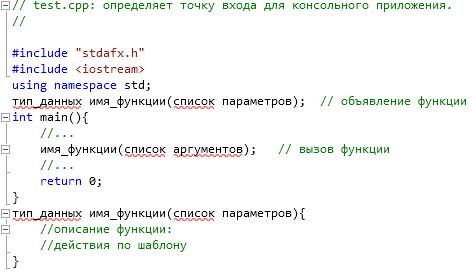
Рис. 5 Описание пользовательской функции после функции main()

Конечно, приведенные выше варианты не заработают, т.к. они показывают общую структуру записи программ. В наших примерах всегда будем использовать первый вариант.

Вообще говоря, любую функцию следует воспринимать как некий воображаемый аппарат для выполнения какой-либо работы. При этом аппарату нужно работать над каким-то материалом, т.е. входными данными, известными заранее. Этими данными являются параметры функции. Когда аппарат получил материал, то начинает свою работу. Какую именно работу он будет выполнять с входным материалом, зависит от шаблона, т.е. от описания функции. После того, как вся работа будет выполнена, аппарат выдаст нам результат своей работы, некий ответ. Это то, ради чего мы и создавали этот аппарат. Схемотично данный процесс представлен на рис. 6.

Рис. 6 Принцип работы пользовательской функции

Например, для известной нам функции sin(x) из библиотеки <math.h>, входными данными является один параметр – вещественное число х, сам аппарат представляет собой процесс вычисления синуса от х, результатом является полученное значение синуса. Результат является вещественным числом, которое задается ключевым словом double. Поэтому можно было бы представить объявление и описание функции sin(x) следующим образом:

double sin(double x){

double res;

res=...; // вычисление синуса по сложной математической формуле

return res; // ответ, результат

}

Здесь внутри функции объявлена локальная переменная double res, в которую будет насчитываться ответ (res – result – результат). Данная переменная будет видна только внутри пользовательской функции. Переменная res – это, своего рода, временная переменная для расчета синуса. Строка return res; выдает в ответ вычисленное значение синуса.

Вызов функции sin(x) внутри функции main() выглядит следующим образом:

z=sin(1.5);

Примечание. Хотелось бы обратить внимание на разницу между списком параметров при объявлении функции и список аргументов при вызове функции. Объявление, описание и список формальных параметров составляют весь шаблон. Здесь параметры представляют собой некие абстрактные параметры, которые пока нельзя «пощупать». А вот когда идет вызов функции, абстрактные параметры приобретают вполне реальные формы и становятся аргументами функции, конкретными числами. В программе это отражается следущим образом. Объявление и описание функции делается один раз:

double function(double a, double b){...}

Вызовов функции может быть сколько угодно:

int main(){

double x, y, z1, z2, z3;

x=10;

y=-0.3;

z1=function(x,y); // первый вариант вызова

z2=function(1.8, y); // второй вариант вызова

z3=function(1.8, 0); // третий вариант вызова

return 0;

}

Рассмотрим несколько примеров по созданию пользовательских функций.

Пример 1. Требуется создать пользовательскую функцию для вычисления квадрата вещественного числа.

Решение. Составим схему работы нашей пользовательской функции в общем виде на рис 7.

Рис. 7 Схема в общем виде для примера 1

Т.к. параметр х должен быть вещественным, то ему соответствует тип double. Пользовательская функция должна считать квадрат числа, поэтому назовем ее kv. В ответ будет выдаваться вещественное число, поэтому возвращаемый тип у функции будет double.

Объявление и описание функции kv:

double kv(double x){

double res;

res=x*x;

return res;

}

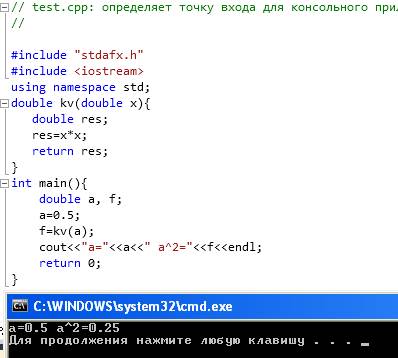
Код программы и результат выполнения программы:

Пример 2. Вычислить таблицу «x, Z» значений функции 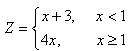при -1≤х≤2 с шагом 1.

Решение. Сделаем пользовательскую функцию для вычисления значения функции Z(x). Возвращаемый тип – double, т.к. ответом является вещественное число. Параметр один, double x. В описании пользовательской функции будет вычисление функции по разветвляющемуся алгоритму. В функции main() реализуем циклический алгоритм для вывода таблицы значений функции.

Код программы:

// test.cpp: определяет точку входа для консольного приложения.

//

#include "stdafx.h"

#include <iostream>

#include <iomanip>

using namespace std;

double fz(double x){

double res;

if(x<1){

res=x+3.0;

}

else {

res=4.0*x;

}

return res;

}

int main(){

double x, z;

cout<<setw(10)<<"x"<<setw(10)<<"z"<<endl;

for(x=-1; x<=2; x=x+1){

z=fz(x);

cout<<setw(10)<<x<<setw(10)<<z<<endl;

}

return 0;

}

Результат выполнения программы:

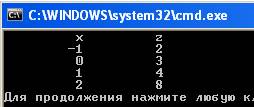
Пример 3. Вычислить таблицу «x, y, Z» значений функции 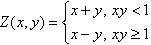при -1≤х≤0,5 с шагом 1, 5≤y≤15 с шагом 5 .

Решение. Сделаем пользовательскую функцию для вычисления значения функции Z(x). Возвращаемый тип – double, т.к. ответом является вещественное число. Параметров два, double x, double y. В описании пользовательской функции будет вычисление функции по разветвляющемуся алгоритму. В функции main() реализуем вложенные циклы для вывода таблицы значений функции.

Код программы:

// test.cpp: определяет точку входа для консольного приложения.

//

#include "stdafx.h"

#include <iostream>

#include <iomanip>

using namespace std;

double fz(double x, double y){

double res;

if(x*y<1){

res=x+y;

}

else {

res=x-y;

}

return res;

}

int main(){

double x, y, z;

cout<<setw(10)<<"x"<<setw(10)<<"y"<<setw(10)<<"z"<<endl;

for(x=-1; x<=0.5; x=x+1){

for(y=5; y<=15; y=y+5){

z=fz(x, y);

cout<<setw(10)<<x<<setw(10)<<y<<setw(10)<<z<<endl;

}

}

return 0;

}

Результат выполнения программы:

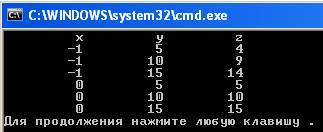
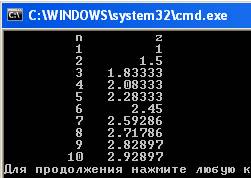
Пример 4. Вычислить таблицу значений функции 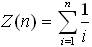при 1≤n≤10 с шагом 1.

Решение. Сделаем пользовательскую функцию для вычисления значения функции Z(n). Возвращаемый тип – double, т.к. ответом является вещественное число. Параметр один, int n. В описании пользовательской функции будет вычисление функции по циклическому алгоритму. В функции main() реализуем цикл по n для вывода таблицы значений функции.

Код программы:

// test.cpp: определяет точку входа для консольного приложения.

//

#include "stdafx.h"

#include <iostream>

#include <iomanip>

using namespace std;

double fz(int n){

double res;

int i;

res=0;

for(i=1; i<=n; i=i+1){

res=res+1.0/i;

}

return res;

}

int main(){

int n;

double z;

cout<<setw(10)<<"n"<<setw(10)<<"z"<<endl;

for(n=1; n<=10; n=n+1){

z=fz(n);

cout<<setw(10)<<n<<setw(10)<<z<<endl;

}

return 0;

}

Результат выполнения программы:

Пример 5. Создать пользовательскую функцию для вывода массива из 5 строк и 5 столбцов на экран.

Решение. Пользовательскую функцию назовем print_mass. В качестве параметра будет сам массив, например, double х[5][5]. Результатом пользовательской функции является вывод массива на экран, поэтому никакого числа в ответе не будет. Следовательно, возвращаемый тип на этот раз будет void, что означает «пустой». В описании пользовательской функции организуем вывод двумерного массива во вложенном цикле. В функции main() инициализируем два массива A[5][5], B[5][5] и вызовем функцию print_mass два раза.

Код программы:

// test.cpp: определяет точку входа для консольного приложения.

//

#include "stdafx.h"

#include <iostream>

#include <iomanip>

using namespace std;

void print_mass(double x[5][5]){

int i, j;

for(i=0; i<5; i=i+1){

for(j=0; j<5; j=j+1){

cout<<setw(10)<<x[i][j];

}

cout<<endl;

}

}

int main(){

double A[5][5], B[5][5];

int i,j;

for(i=0; i<5; i=i+1){

for(j=0; j<5; j=j+1){

A[i][j]=2.3*i+j;

B[i][j]=i-1.5*j;

}

}

cout<<"massiv A:"<<endl;

print_mass(A);

cout<<"massiv B:"<<endl;

print_mass(B);

return 0;

}

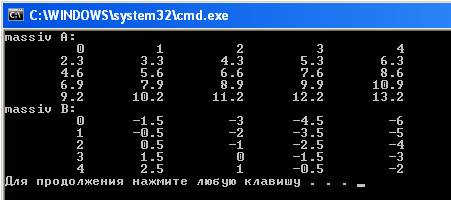
Результат выполнения программы:

Пример 6. Массив А[5][5] задан по формуле А[i][j]=0,3i-j, массив B[5][5] по формуле B[i][j]=i-1.5j. Вычислить сумму положительных элементов массивов.

Решение. Создадим пользовательскую функцию для вычисления суммы положительных элементов массива, назовем ее sum_pol. В качестве параметра будет формальный массив x[5][5]. В функции main() проинициализируем массивы A и B, затем два раза вызовем функцию sum_pol.

Код программы:

// test.cpp: определяет точку входа для консольного приложения.

//

#include "stdafx.h"

#include <iostream>

#include <iomanip>

using namespace std;

double sum_pol(double x[5][5]){

int i, j;

double s;

s=0;

for(i=0; i<5; i=i+1){

for(j=0; j<5; j=j+1){

if(x[i][j]>0){ s=s+x[i][j];}

}

}

return s;

}

int main(){

double A[5][5], B[5][5], sa, sb;

int i,j;

for(i=0; i<5; i=i+1){

for(j=0; j<5; j=j+1){

A[i][j]=0.3*i+j;

B[i][j]=i-1.5*j;

}

}

sa=sum_pol(A);

cout<<"s A>0 = "<<sa<<endl;

sb=sum_pol(B);

cout<<"s B>0 = "<<sb<<endl;

return 0;

}

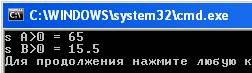
Результат выполнения программы:

Краткие итоги:

Чтобы работать с файлами, необходимо использовать переменную типа fstream. Рассмотрены случаи вывода в файл и чтения из файла.

Вопросы:

1. Что такое файловый поток?

2. Что необходимо сделать, чтобы использовать в программе файловый поток?

3. Как сделать разделение по ячейкам при записи в файл *.xls?

4. Что такое пользовательская функция?

5. Что такое объявление, описание, вызов пользовательской функции?

Упражнения:

1. Составьте программу, которая создаст следующие файлы:

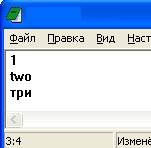
2. Составьте блок-схему и программу для построения таблицы значений функции Z(x, y)=5,5x-2,8y при 0≤x≤1 с шагом 0,2; -2≤y≤0 с шагом 0,8. Таблицы вывести на экран, в файлы *.txt, *.xls.

3. Для массива X(15) найти минимальный элемент, максимальный элемент; найденные минимальный и максимальный элементы поменять местами. Исходный массив X(15) считать из файла. Исходный массив, результаты вычислений и измененный массив вывести на экран и в файл *.xls.

4. Составить блок-схему и программу для вычисления суммы 20 чисел из файла. Указание: использовать циклический алгоритм, не использовать массивы.

5. В программе для задачи 3 создать пользовательские функции для вычисления минимального и максимального элементов.

6. Массив А(10) считать из файла. Вывести массив А на экран. Поменять местами первый и последний элементы. Измененный массив вывести на экран. Указание: для вывода массива на экран создать пользовательскую функцию.