Задание 2

Пролог для задач искусственного интеллекта

Постановка задачи

Разработать пролог-программу, решающую определенную вариантом задания задачу из области искусственного интеллекта с использованием методов этой области: различных алгоритмов перебора и способов ограничения перебора на основе эвристической информации (альфа-бета процедура, эвристическое отсечение ветвей дерева перебора и др.).

Требования к исполнению

1. В вариантах заданий, предполагающих для поиска нужного решения задачи перебор с возвратом, необходима эффективная программная реализация этого перебора.

2. Программа должна быть организована как законченная система с удобным и понятным интерфейсом, для этого следует предусмотреть:

- повторное выполнение основных функций системы после редактирования исходных данных;

- сохранение исходных данных во внешнем файле;

- выдачу необходимых в текущий момент подсказок и пояснений;

- досрочное окончание работы пользователя с системой.

3. В вариантах заданий, в которых возможно несколько различных решений (для одних и тех же исходных данных), необходимо организовать случайный выбор одного из таких решений.

Варианты задания

1. Система, отвечающая на вопросы о родственных отношениях

Основным модулем системы должна быть база знаний, в которой хранится информация о членах (не менее 15-20 человек) семьи из нескольких (не менее 4-х) поколений и родственных отношениях между ними. Системе должны быть известны не менее 12-15 различных родственных отношений. Некоторые отношения - базовые - должны быть представлены в базе явно - в виде соответствующих фактов Пролога, например, к числу базовых отношений могут быть отнесены понятия «родитель», «супруги», «мужчина» и «женщина». Важно, что к базовым отношениям могут быть сведены все остальные отношения родства, например, «внук», «дядя», «невестка». Поэтому остальные отношения должны быть представлены в базе знаний неявно, т.е. должны выводиться пролог-процедурами исходя из базовых отношений. Таким образом, база знаний должна быть дедуктивной (т.е. обладать возможностями дедуктивного вывода).

Отметим, что базовый набор отношений может быть выбран не единственным способом: например, вместо бинарного отношения «родитель» могут быть взяты отношения «мать» и «отец».

В возможности системы входят:

· ответы на запросы, которые могут быть двух видов:

1. определить для двух конкретных членов семьи, в каком родственном отношении они находятся, например: «В каком родстве Елена и Петр?»;

2. определить для заданного члена семьи, кто состоит с ним в конкретном родственном отношении, например: «Кто является тетей Ольги?» или «Кто внуки Андрея?».

· модификация в диалоге с пользователем базы знаний: введение в нее новой информации о членах семьи и коррекция старой информации.

В случае ввода новых утверждений - отношений, не являющихся базовыми, они должны быть «разложены» на более простые утверждения с помощью базового набора отношений, которые и записываются в базу знаний.

Заметим, что при вопросах первого вида, если разница поколений заданных членов семьи превышает 2 поколения, необходимо в ответе произвести синтез искомого отношения из нескольких известных системе отношений, например: «Елена - сестра внука Петра» или «Елена - сестра Николая, внука Петра».

Предполагается, что все лица (члены семьи), известные системе, имеют разные имена - это необходимо для корректной работы системы. Чтобы исключить противоречия в базе знаний, желательно, чтобы при вводе пользователем новой информации система проверяла ее на непротиворечивость по отношению к текущему состоянию базы знаний и осуществляла только ввод допустимых фактов. Например, факт «Женя - дочь Андрея» недопустим, если в базе знаний хранится информация о том, что Женя - муж Ольги.

Интерфейс с пользователем может быть организован с помощью стандартных средств: меню, форматов для ввода, или же простейшего синтаксического анализа запросов с помощью ключевых слов [Ин, с.452‑472].

Для соблюдения правил русского языка при выводе ответов на вопросы пользователя можно встроить в систему достаточно полный список имен, с указанием их именительного и родительного падежей (именно эти падежи используются в естественно-языковых фразах-вопросах указанных выше видов и ответах на них).

2. Программа синтаксического анализа предложений естественного языка

Предлагается рассмотреть некоторый ограниченный подъязык письменной речи одного из европейских языков (русский, английский, испанский и проч.).

Входящие в такой подъязык предложения состоят в общем случае из группы подлежащего (именной группы) и группы сказуемого (глагольной группы). Группа подлежащего в свою очередь состоит из артикля, нескольких прилагательных и/или числительных, а также существительного или местоимения, а группа сказуемого - из глагола в одной из личных форм и нескольких дополнений или обстоятельств в виде именных групп (с предлогом или без). Приведем пример подобного предложения: «Маленький мальчик долго играл с черной собакой в саду».

Необходимо зафиксировать структуру подъязыка с помощью некоторого обобщения контекстно-свободной грамматики [Стерлинг, с. 203-210; Клоксин, с. 234-255; Ин, с.473-488]. Грамматика должна учитывать согласование в лице и числе именной группы в роли подлежащего и глагольной группы в роли сказуемого и, возможно, согласование составных частей самой именной группы.

Построенная на базе указанной грамматики пролог-программа должна производить синтаксический анализ (разбор) поступающего на вход предложения естественного языка, а также строить и визуализировать дерево разбора этого предложения. Встроенный в программу словарь слов (или основ) выбранного естественного языка должен включать не менее 20 единиц для каждой части речи (существительное, прилагательное, глагол и т.п.) и допускать расширение. Реализацию синтаксического анализа следует осуществить эффективно, с использованием разностных списков или других разностных структур.

Можно рассмотреть усложнение рассмотренного варианта задания - создание пролог-программы, результатом синтаксического анализа которой является не дерево разбора, а эквивалентное по смыслу предложение другого естественного языка. Фактически такая программа производит перевод предложения с одного естественного языка на другой (например, с английского на французский). Для такого усложнения следует брать пару родственных языков. При выполнении задания кроме описывающей первый язык формальной грамматики потребуется также набор продукций вида: грамматическая конструкция первого языка ® грамматическая конструкция второго языка.

3. Экспертная система классификации объектов

(диагностического типа )

Назначение экспертной системы (ЭС) - проведение диалога-консультации, состоящего из нескольких вопросов к пользователю о наблюдаемых признаках некоторого объекта, и затем решение на основе ответов пользователя, к какому классу (типу, виду) принадлежит этот объект, например, на основе внешних признаков музыкального инструмента (размера, формы, наличия клавишей, струн, смычка и т.п.) система определяет вид музыкального инструмента (скрипка, балалайка, рояль и др.).

Основными модулями экспертной системы являются [Братко, с. 414-421]:

· база знаний, состоящая из продукций (правил вывода) вида:
условие ® следствие, каждая из которых воплощает некоторый фрагмент знания, необходимый для классификации объектов (т.е. знания в конкретной проблемной области);

· механизм вывода (решатель), который осуществляет поиск решения - нужной (решающей) цепочки продукций, представляющей последовательные шаги заключения о классе объекта.

Важно, что полученное системой решение (о классе объекта) при необходимости может быть пояснено пользователю - это одна из отличительных особенностей ЭС. Для этого экспертная система должна уметь отвечать на вопросы вида «как?» и «почему?».

Вопросы «как?» (т.е. как получено указанное решение?) задаются по окончании диалога-консультации, в качестве ответа система визуализирует решающую цепочку продукций. Вопросы «почему?» (т.е. почему запрашивается этот признак?) могут быть заданы в ходе диалога, в ответ система показывает правило продукции, которое она пробует в текущий момент применить. Модуль ЭС, реализующий такие поясняющие ответы, называют подсистемой объяснения.

Вывод решения (поиск решающей цепочки) может производиться в прямом направлении: от известных фактов, т.е. наблюдаемых признаков объекта, к следствиям - заключениям о классе или подклассе объекта (так называемый прямой вывод - см. [Ин, с. 406-444] ), или же наоборот - от гипотез о возможном классе или подклассе объекта к фактам, их подтверждающим (так называемый обратный вывод - см. [Братко, с.426‑455]).

Поскольку в процессе вывода выявляются обычно недостающие для нужного заключения факты, которые необходимо запросить у пользователя, то ход диалога-консультации определяется фактически механизмом вывода и набором правил из базы знаний. В силу этого интерфейс с пользователем часто не выделяют в отдельный модуль, а относят к механизму вывода.

В качестве возможной проблемной области (области экспертизы) может быть взята классификация плодов (признаки: цвет, форма, вкус, количество косточек и проч.), грибов (признаки: цвет шляпки, толщина ножки, наличие пятен в окраске, особенности роста - отдельно, группой и проч.), пород собак (признаки: вид и длина шерсти, размер, масть, тип ушей - стоячие, лежачие и проч.), а также транспорта, оружия, бабочек, автомобилей, напитков и т.п. Мощность базы знаний должна позволять экспертной системе распознавать на менее 25 различных классов объектов по нескольким (не менее пяти) признакам.

4. Программа, составляющая головоломку крисс-кросс (перекрестный кроссворд)

Рассматриваемая головоломка крисс-крос предлагает задачу более простую, чем кроссворд, а именно: заданы набор слов и схема, подобная сетке кроссворда. В эту схему необходимо вписать все слова. Схема состоит из пересекающихся, но не соприкасающихся вертикальных и горизонтальных линий из клеток [Уэзерелл, с. 55-56], причем схема должна быть связной - см. рисунок 4.

				К
З	О	О	П	А	Р	К
Е				Б		О	С	Е	Л
Б	Е	Л	К	А		Т		Ж
Р		И		Н
А	И	С	Т
		А

	Рис. 4

Программа составления головоломки, получая на вход набор из 7-15 различных слов одного из естественных языков - русского или английского - должна построить подходящую для них схему или несколько схем. Схема построена правильно, если она связная и все слова могут быть вписаны в нее, причем допускается лишь один вариант ее заполнения, т.е. головоломка имеет единственное решение.

Если для данного списка слов не существует решения-схемы, то программа должна сообщить об этом, указав по возможности причину неудачи (например, наличие слова, «непересекающегося» с другими словами). В остальных случаях построенная схема должна быть изображена на экране компьютера (в текстовом или графическом режиме), и по желанию пользователя может быть показано решение головоломки, т.е. заполнение схемы исходными словами.

В случаях, когда для заданного набора слов возможно несколько схем, предпочтение следует отдавать более качественным решениям, т.е. более компактным и связным схемам. Связность схем зависит от количества пересечений в ней, она может определяться как среднее или минимальное число пересечений на слово. Компактность схемы определяется площадью наименьшего объемлющего ее прямоугольника. Указанный эвристический критерий качества схемы рекомендуется формализовать тем или иным способом (возможно, в виде эвристической функции) и использовать при поиске правильных схем.

Отметим, что длина слов из заданного набора и количество слов одинаковой длины служат важным ключом как к разгадке самой головоломки, так и к написанию программы их составления. Оптимальная организация перебора вариантов схем при поиске программой правильной схемы требует установления определенного порядка, в каком будут рассматриваться слова исходного набора: имеет смысл применить эвристическое упорядочивание набора и переупорядочивание нерассмотренных слов на любом шаге поиска, а также эвристическое отсечение части вариантов схем, поскольку в иных случаях перебор может оказаться слишком большим. Проверку же требования единственности решения головоломки целесообразно проводить как можно раньше, чтобы исключить лишнюю работу (построение до самого конца вариантов схем, допускающих несколько решений головоломки).

5. Программа построения прямоугольного лабиринта

Рассмотрим лабиринты, расположенные в прямоугольной области M ´ N (5£M, N£30) и состоящие из стенок внутри и на границе этой области. Стенки являются сторонами некоторых квадратов (клеток) из покрывающей эту область равномерной сетки [Уэзерелл, с.57-58]. Лабиринты имеют один вход - на одной из сторон прямоугольной области и один выход - на противоположной стороне. Такой лабиринт может быть получен из равномерной сетки стенок в результате выбивания ровно двух граничных стенок на противоположных сторонах рассматриваемого прямоугольника и удаления некоторого количества внутренних стенок (см. рисунок 5).

Þ
Þ

	Рис. 5

Лабиринт проходим, если внутри него между стенками существует путь, соединяющий вход и выход. Будем говорить в этом случае, что лабиринт имеет решение. Решение единственно, если среди всех таких путей есть минимальный по длине путь, являющийся частью всех остальных путей. Клетка лабиринта достижима, если существует путь, соединяющий ее с входом или выходом. Тот факт, что все клетки лабиринта достижимы, означает, что в лабиринте отсутствуют замкнутые (стенками) области из клеток.

Требуемая пролог-программа должна по заданным M и N строить прямоугольный лабиринт, который имеет единственное решение и состоит только из достижимых клеток. Программа должна визуализировать построенный лабиринт, отметить вход и выход и по указанию пользователя показать путь между ними.

При каждом обращении к программе, даже с одними и теми же значениями M и N, она должна порождать разные лабиринты. Для этого необходимо в некоторые моменты построения лабиринта производить «случайный» выбор варианта дальнейшего продолжения.

Желательно, чтобы построенный лабиринт был интересным, т.е. содержал извилистые стенки и почти замкнутые области, а решение-путь в нем был достаточно длинным и извилистым, т.е. включал достаточно большое число поворотов.

Заметим, что стратегии генерации лабиринта могут быть различны: возможно не только удаление внутренних стенок в прямоугольной сетке стенок, но и последовательная установка стенок в исходно пустой прямоугольной области. При любой стратегии единственность решения, как и достижимость клеток лабиринта, целесообразно проверять как можно раньше, либо же гарантировать выполнение этих требований самим методом построения лабиринта.

6. Игровая программа

Предлагается выбрать игру из класса игр двух лиц (игроков) с полной информацией [Братко, с.472-475], к которому относятся, например, шахматы и шашки. Игра должна быть достаточно сложной, чтобы практически исключалась возможность полного просмотра дерева игры и обнаружения выигрышной стратегии (если таковая существует), например, шашки без дамок, калах [Уэзерелл, с. 76-78], шахматный эндшпиль, реверси и крестики-нолики на неограниченной доске.

В таких играх для выбора компьютером очередного хода используется так называемая статическая оценочная функция, оценивающая позицию игры как таковую без учета ее продолжений, и альфа-бета процедура поиска наилучшего хода, исходя из заданной игровой позиции [Уэзерелл, с. 78-86; Братко, с. 479-484]. Альфа-бета процедура основана на частичном просмотре возможных продолжений игры на заданное количество D ходов игроков ( т.е. просмотре дерева игры от заданной игровой позиции на глубину D) и оценки возможных игровых позиций (вершин дерева) с помощью статической оценочной функции. В отличие от минимаксной процедуры, решающей ту же задачу, альфа-бета процедура выполняет просмотр дерева и оценку вершин более экономно.

Требуемая игровая программа должна использовать альфа-бета процедуру, оформленную в виде отдельного модуля. Она должна уметь играть как против человека (пользователя), так и против самой себя или другой игровой программы, и при этом визуализировать текущую позицию игры, а ввод ходов игроков осуществлять в наиболее удобной форме.

В программе следует предусмотреть возможность изменения (перед началом игры) глубины D просмотра дерева игры альфа-бета процедурой (2£D£6, шаг глубины соответствует ходу одного игрока), а также - чтобы с программой было интересно играть, случайный выбор хода из нескольких равноценных.

7. Программа генерации геометрических головоломок

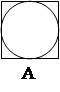
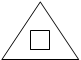
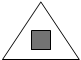
В таких головоломках требуется найти закономерность в наборе из нескольких составных геометрических фигур. Составными элементами каждой фигуры могут быть: точка, квадрат, треугольник, прямоугольник, круг, различные отрезки линий и др. Такие элементы могут быть соединены в фигуре различным образом: они могут быть вложены друг в друга, могут пересекаться или соприкасаться [Стерлинг, с.182-184, 189]. Кроме того, контуры элементов могут быть разного цвета, а их внутренняя часть - заштрихованной или цветной. Примеры наборов таких составных фигур показаны на рисунках 6 и 7. Могут быть и более сложные фигуры - например, схематические изображения человечков или животных.

?

D

Рис. 6

?

Рис. 7

Рис. 8

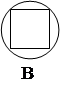Поиск закономерности предполагает обнаружение недостающей фигуры (обозначенной на рисунках вопросительным знаком). В первом случае (рис. 6) необходимо обнаружить аналогию, т.е. найти фигуру D, относящуюся к С, как фигура В - к фигуре А. Во втором случае (рис. 7) требуется найти фигуру, завершающую закономерность.

В обоих рассмотренных видах задачи поиска закономерностей предлагается несколько вариантов ответа , среди которых надо выбрать правильный. Например, возможный для задачи с рисунка 7 набор вариантов ответа показан на рис. 8, правильный ответ этой задачи - фигура 6 на рис. 8. Правильный ответ задачи с рисунка 6 - фигура из треугольника, в который вписан круг.

Программа генерации геометрических головоломок должна сформировать задачу на поиск геометрической закономерности, то есть набор составных фигур без некоторой недостающей фигуры и набор различных составных фигур, включающих эту недостающую фигуру (набор ответов). Программа должна показать сгенерированную задачу пользователю и предложить ему на выбор: либо самому решить задачу (в этом случае она проверяет правильность решения и сообщает о результате пользователю), либо показать ему правильное решение (если он затрудняется задачу решить).

Важно предусмотреть возможность решения пользователем за сеанс работы с программой нескольких задач - для этого программа при каждом обращении к ней должна порождать разные задачи, причем в разные сеансы последовательности генерируемых задач должны быть разными. Чтобы этого достичь, следует в некоторые моменты процесса генерации задачи производить случайный выбор составных элементов фигур и их конфигурации, используя датчик случайных величин и некоторое доступное программе значение, заранее неизвестное (дату и/или текущее время). Для представительности множества генерируемых задач необходимо, чтобы геометрические фигуры задачи включали не менее 5 различных элементов, включая цвет и штриховку.

Программа построения геометрических головоломок должна быть организована таким образом, чтобы допускать быструю перенастройку системы для генерации задач, в которые входят фигуры с другими составными элементами. Такая перенастройка должна осуществляться без переработки пролог-процедуры генерации головоломки - допустимо лишь добавление процедур отрисовки новых элементов фигур.

8. Программа разработки маршрутов транспортных перевозок

Рассматривается сеть одноколейных железнодорожных путей, соединяющих N (5£N£10) городов; известны длины всех путей (дорог) в километрах. Задан некоторый набор из M (3£M£9) заявок на грузоперевозки по этой железной дороге в течение текущих суток. Каждая заявка включает в общем случае следующую информацию:

· пункт (город) отправления грузового состава;

· пункт (город) назначения грузового состава;

· максимальную скорость движения состава по путям (не более 100 км в час);

· час суток, не позднее которого груз должен прибыть в пункт назначения.

Требуемая программа должна составить - исходя из заданного набора заявок - расписание движения грузовых составов, состоящее из М маршрутов. Каждый маршрут соответствует заявке и фиксирует кроме пунктов (городов) отправления и назначения следующее:

· время (в часах) отправления из исходного пункта;

· время (в часах) прибытия в конечный пункт;

· промежуточные пункты, через которые проходит маршрут, и время остановки в них;

· скорость движения на каждом участке пути между промежуточными пунктами маршрута.

Считается, что скорость движения каждого состава на любом участке пути постоянна. Она может быть разной для разных составов и разных участков пути, но не выше указанной в заявке и не ниже 20 км/час. Каждый грузовой состав может делать остановки на промежуточных пунктах маршрута, но они не должны по длительности превышать 3 часа. Через любой город в одно и то же время может проезжать только один состав.

Основное требование, предъявляемое к составлению маршрутов перевозок - протяженность каждого маршрута между заданными городами отправления и назначения не должна превышать минимальное расстояние между ними по этой железной дороге более чем в 1,5 раза.

Программа должна визуализировать карту дорог, на которой затем должны быть высвечены найденные маршруты. Желательно также в динамике показать прохождение грузовых составов по этим маршрутам в течение суток (шаг пересчета местонахождения составов - 0,5 часа).

9. Программа составления учебного расписания

Назначение программы - составление недельного расписания занятий для курса, включающего K (7£ K £12) студенческих групп. Исходной информацией для составления расписания являются:

· учебный план курса, определяющий названия изучаемых предметов (не более 7 разных), и количество учебных занятий в неделю для изучения каждого предмета (не более 5 занятий в неделю);

· список-распределение преподавателей по группам, в котором для каждой учебной группы и каждого изучаемого предмета указывается фамилия преподавателя, который будет вести этот предмет в этой группе.

Известно, что суммарное количество учебных занятий по учебному плану не превышает 19 занятий в неделю, а недельная нагрузка каждого преподавателя не превышает 7 занятий.

При генерации расписания для студенческих групп желательно более или менее равномерное распределение занятий по дням недели (от понедельника до субботы включительно). Оптимальным следует считать 2-3 занятия в день. В составленном расписании должны быть выполнены следующие требования:

1. В каждый день недели у любой учебной группы не может быть больше четырех занятий, а у любого преподавателя - больше трех занятий;

2. В каждый день недели у любой группы по расписанию не может быть больше одного «окна» (перерыва) между занятиями, причем протяженность «окна» - не более чем одно занятие;

3. Для каждого преподавателя определяемое расписанием распределение его учебной нагрузки по дням недели должно быть достаточно «плотным», т.е. в нем не должно быть более одного дня всего лишь с одним занятием, а «окна» между занятиями в каждый учебный день в сумме не должны быть больше двух занятий.

Основным результатом работы программы является построенное учебное расписание занятий для всех групп, определяющее для каждой группы и каждого учебного дня все занятия этого дня. Для каждого занятия в расписании должны быть заданы: номер и время начала занятия, предмет, фамилия преподавателя. Возможные номера занятий - от 1 до 6, они обозначают порядок следования по времени в течение дня указанных занятий: например, за номером 1 может быть закреплено время 9.00, за номером 2 - 11.00 и т.д.

Составленное учебное расписание группы должно быть в понятном и обозримом виде выведено на экран компьютера. Необходимо также предусмотреть возможность вывода (показа) определяемого этим расписанием индивидуального расписания каждого преподавателя, т.е. распределения по дням его учебной нагрузки. Это расписание для каждого учебного дня указывает, есть ли занятия в этот день, и если есть, то для каждого занятия - их номер и время, предмет, номер группы.