Разветвляющаяся алгоритмическая конструкция
Пример 2. Алгоритм вывода значения наибольшего из двух чисел.
Постановка задачи: вывести значение наибольшего из двух заданных чисел.
Исходные данные: а, b – два числа из области действительных значений.
Выходные данные: наибольшее из заданных чисел а, b.
Псевдокод алгоритма:
1. Начало.
2. Ввод двух чисел а, b.
3. ЕСЛИ а > b, ТО «вывести а»,
ИНАЧЕ «вывести b».
4. Конец.
Блок-схема алгоритма представлена на рисунке 3.13.
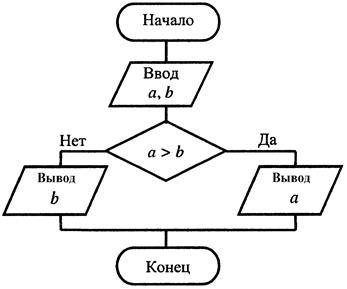
Рисунок 3.13 Блок-схема алгоритма к примеру 2.
Пример 3. Алгоритм поиска наименьшего значения среди трех заданных (неполная разветвляющаяся алгоритмическая конструкция).
Постановка задачи: Заданы три числа. Вывести значение наименьшего из них.
Исходные данные: а, b, c – три числа из области действительных значений.
Выходные данные: min – значение наименьшего из заданных чисел.
Псевдокод алгоритма:
1. Начало.
2. Ввод трех чисел а, b, с.
3. Присвоить результирующему наименьшему значение первого из заданных чисел min=a.
4. ЕСЛИ b < min, ТО min=b,
ИНАЧЕ «перейти к п.5».
5. ЕСЛИ с < min, ТО min=с,
ИНАЧЕ «перейти к п.6».
6. Вывести min.
7. Конец.
Блок-схема алгоритма представлена на рисунке 3.14.
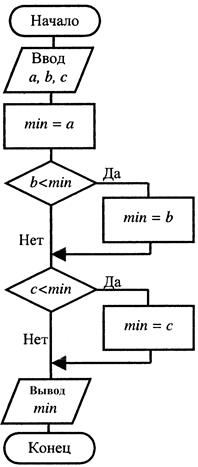
Рисунок 3.14 Блок-схема алгоритма к примеру 3.
Алгоритмическая конструкция «цикл»
Пример 4. Алгоритм нахождения наибольшего общего делителя двух натуральных чисел (алгоритмическая конструкция «цикл с предусловием»).
Постановка задачи: определить наибольший общий делитель двух натуральных чисел.
Исходные данные: m, n – два числа принадлежащие ряду натуральных чисел.
Выходные данные: значение наибольшего общего делителя.
Псевдокод алгоритма:
1. Начало.
2. Ввод натуральных чисел m и n.
3. Пока m¹n выполнять:
4. ЕСЛИ m > n ТО m = m - n,
ИНАЧЕ n = n - m.
5. Переход к п3.
6. Вывод m (найденный наибольший общий делитель).
7. Конец.
Блок-схема алгоритма представлена на рисунке 3.15.
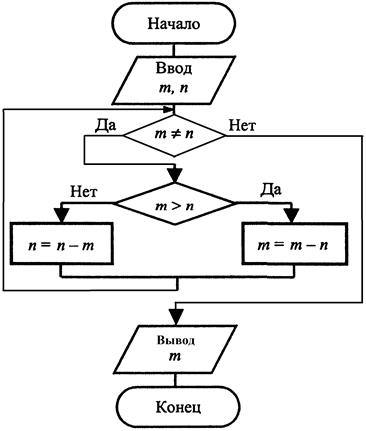
Рисунок 3.15 Блок-схема алгоритма к примеру 4.
Пример 5. Алгоритм игры «Угадай число» (алгоритмическая конструкция «цикл с постусловием»).
Постановка задачи: Первый игрок вводит задуманное число от 1 до 50. Второй (угадывающий) вводит другое число и получает один из ответов: «Ваше число меньше», «Ваше число больше» или «Вы угадали». Игра продолжается до тех пор, пока второй игрок не угадает задуманное число.
Исходные данные: х – задуманное первым игроком натуральное число, принадлежащее диапазону от 1 до 50, у – число, вводимое на очередном шаге вторым игроком.
Выходные данные: сообщения второму игроку.
Псевдокод алгоритма:
1. Начало.
2. Ввод числа х.
3. Ввод числа y.
4. ЕСЛИ x > y ТО вывести сообщение «Ваше число меньше» и перейти к п.3
ИНАЧЕ перейти к п.5
5. ЕСЛИ x < y ТО вывести сообщение «Ваше число больше» и перейти к п.3
ИНАЧЕ перейти к п.6
6. Вывести сообщение «Вы угадали»
7. Конец.
Блок-схема алгоритма представлена на рисунке 3.16.
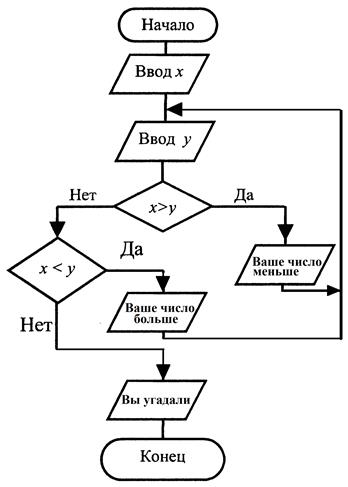
Рисунок 3.16. Блок-схема алгоритма к примеру 5.
Пример 6. Алгоритм вычисления суммы (алгоритмическая конструкция «арифметический цикл»).
Постановка задачи: Для заданного натурального числа N вычислить сумму 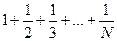
Исходные данные: N – натуральное число.
Выходные данные: S – результирующая сумма.
Формульно-символьное описание алгоритма:
1. Начало.
2. Ввод N.
3. Задать начальное значение суммы S=0.
4. Для i = 1, N, 1 повторить
4.1. 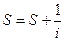
5. Вывод S.
6. Конец.
Блок-схема алгоритма представлена на рисунке 3.17.
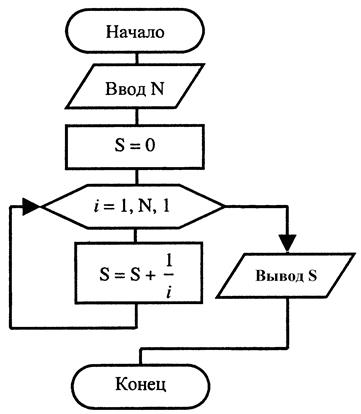
Рисунок 3.17. Блок-схема алгоритма к примеру 6.
