Полностью самопроверяемые цифровые устройства

Рассмотрим контролируемое цифровое устройство (КУ на рис. 4.24), которое имеет m входов и n выходов. Функционирование КУ отличается некоторой закономерностью, которая позволяет выделить правильные вы­ходные наборы, соответствующие работе КУ без неисправностей, из об­щей совокупности возможных выходных наборов. Для определения пол­ноты контроля вводят понятие самопроверяемости [3].

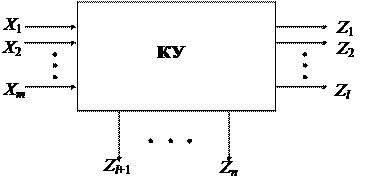Рис. 4.24. Структурная модель контролируемого устройства

Пусть А = {a} – множество рабочих входных наборов КУ, a = {x₁,... ..., x_m}, S – множество неисправностей в КУ, В = {b} – множество выход­ных наборов исправного устройства, b = {z₁,..., z_n}, в состав выходов вклю­чаются рабочие выходы устройства {z₁,..., z_i} и дополнительные выходы {z_i+1, ..., z_n}, необходимые для контроля (например, состояния элементов памяти), G(a, S_i) – выход КУ при наличии неисправности s_i принадлежит S, G(a, 0) – выход исправного КУ.

Цифровое устройство защищено от неисправностей множества S, если для любого рабочего входного набора и любой неисправности выход устройства с неисправностью, либо не отличается от исправного, либо не совпадает ни с одним правильным выходным набором КУ.

Цифровое устройство называется самотестируемым по отношению к множеству неисправностей S, если для любой неисправности существует такой рабочий входной набор, что выход устройства не совпадает ни с од­ним выходным набором исправного устройства.

Цифровое устройство является полностью самопроверяемым, если оно как защищено от неисправностей, так и самотестируемо.