Линейные вычислительные алгоритмы

АННОТАЦИЯ

Учебное пособие по дисциплине «Теория алгоритмов» предназначено для студентов Политехнического колледжа НовГУ, обучающихся по специальности 230115 «Программирование в компьютерных системах».

Учебное пособие включает введение, два раздела, заключение, список литературы. В разделе 1 рассматриваются понятия алгоритма и вспомогательного алгоритма, основные алгоритмические структуры, формализация понятия «алгоритм» на примерах виртуальных машин Поста и Тьюринга. Раздел 2 посвящен методам построения алгоритмов, таким как рекурсивный метод, методы сортировки данных. Раскрыты идеи линейного и бинарного поиска, а так же методы вычисления сложности алгоритмов.

Каждый из разделов пособия содержит теоретический материал с подробно разобранными примерами. Алгоритмы решения задач представлены в виде блок-схем. Для закрепления материала в конце каждого раздела предложены задачи для самостоятельного решения.

В конце учебного пособия в Приложении представлена рабочая программа дисциплины «Теория алгоритмов» и тексты программ разобранных примеров.

Количество страниц – 77

Количество иллюстраций – 19

Количество таблиц – 3

Количество приложений – 1

Количество библиографических источников - 13

ABSTRACT

Training manual on "Theory of algorithms" is intended for students of the Polytechnic College of the Novgorod state University, students majoring 230115 Programming in computer systems".
The manual includes an introduction, two chapters, conclusions, list of references. Section 1 discusses the concept of algorithm and auxiliary algorithm, the basic algorithmic patterns, formalization of the notion of "algorithm" on the examples of virtual machines, Post and Turing. Section 2 is devoted to methods of constructing algorithms, such as recursive method, methods of sorting data. Uncovered ideas of linear and binary search, as well as methods of computation complexity of algorithms.
Each section of the manual contains theoretical material is covered in detail with examples. The algorithms for solving problems presented in the form of block diagrams. To consolidate the material at the end of each section of the proposed tasks for independent solving.
At the end of the textbook in the Appendix presents the working program of the discipline "Theory of algorithms" and the disassembled code example.

Number of pages - 77

The number of illustrations - 19

Number of tables - 3

The number of applications is - 2

The number of bibliographic sources - 12

Оглавление

ВВЕДЕНИЕ.. 5

1 ОСНОВЫ АЛГОРИТМИЗАЦИИ.. 7

1.1 АЛГОРИТМЫ И ВЕЛИЧИНЫ... 7

1.2 ЛИНЕЙНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ... 15

1.3 ВЕТВЛЕНИЕ В ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМАХ.. 16

1.4 ЦИКЛЫ В ВЫЧИСЛИТЕЛЬНЫХ АЛГОРИТМАХ.. 18

1.5 МАШИНА ПОСТА.. 24

1.6 МАШИНА ТЬЮРИНГА.. 28

1.7 ВСПОМОГАТЕЛЬНЫЕ АЛГОРИТМЫ... 31

1.8 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ... 36

2. МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ.. 48

2.1 РЕКУРСИВНЫЕ МЕТОДЫ ПОСТРОЕНИЯ АЛГОРИТМОВ.. 48

2.2 МЕТОДЫ СОРТИРОВКИ ДАННЫХ.. 51

2.3 МЕТОДЫ ПЕРЕБОРА В ЗАДАЧАХ ПОИСКА.. 62

2.4 СЛОЖНОСТЬ АЛГОРИТМОВ.. 67

2.5 ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ... 73

ЗАКЛЮЧЕНИЕ.. 76

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ... 77

ПИЛОЖЕНИЕ 1. КОМПАКТ-ДИСК С ПРОГРАММАМИ РАССМОТРЕННЫХ В ПОСОБИИ ПРИМЕРОВ.. 78

ВВЕДЕНИЕ

Моделирование является одним из способов познания мира. Для различных явлений и процессов могут быть использованы разные способы моделирования. Объект, который получается в результате моделирования, называется моделью. Видов моделей достаточно много, например:

Математические модели- знаковые модели, описывающие определенные числовые соотношения.

Графические модели - визуальное представление объектов. Здесь наглядность модели выходит на первый план.

Имитационные модели – модели, позволяющие наблюдать изменение поведения элементов системы, проводить эксперименты, изменять отдельные параметры модели.

Быстрое развитие вычислительной техники и широкое распространение персональных компьютеров открывает перед моделированием огромные перспективы для исследования процессов и явлений окружающего мира.

Компьютерное моделирование – это моделирование, реализуемое с помощью компьютерной техники.

Компьютерное моделирование тесно связано с понятием «алгоритм» и его свойствами, которое, в свою очередь, является объектом исследования науки об алгоритмах – теории алгоритмов. Теория алгоритмов является основой программирования и информатики.

На сегодняшний день выбор научной и учебной литературы по теории алгоритмов очень многообразен, однако, достаточно трудно найти учебные пособия, которые были бы рассчитаны на небольшое количество часов курса и в то же время могли раскрыть основные идеи и методы теории алгоритмов. Этим и обусловлена актуальность разработки данного учебного пособия по дисциплине «Теория алгоритмов».

Учебное пособие «Теория алгоритмов» разработано в соответствии с:

• Федеральным государственным образовательным стандартом по специальности 230115 «Программирование в компьютерных системах»;

• Рабочей программой дисциплины «Теория алгоритмов».

В результате изучения дисциплины «Теория алгоритмов» студент должен:

Уметь:

- разрабатывать алгоритмы для конкретных задач;

- определять сложность работы алгоритмов.

Знать:

- основные модели алгоритмов;

- методы построения алгоритмов;

- методы вычисления сложности работы алгоритмов.

Целью данного учебного пособия является изучение и применение в дальнейшей профессиональной деятельности основ и методов теории алгоритмов.

Учебное пособие состоит из введения, двух разделов, заключения и списка литературы. В первом разделе рассматриваются понятия алгоритма и вспомогательного алгоритма, основные алгоритмические структуры, виды алгоритмов, формализация понятия «алгоритм» на примерах виртуальных машин Поста и Тьюринга. Второй раздел учебного пособия освещает методы построения алгоритмов, а именно, рекурсивный метод, метод сортировки данных и методы поиска информации. Для успешного усвоения изученного материала в конце каждого раздела предложены задания для самостоятельной работы.

ОСНОВЫ АЛГОРИТМИЗАЦИИ

АЛГОРИТМЫ И ВЕЛИЧИНЫ

Слово "алгоритм" произошло от латинской формы имени величайшего среднеазиатского математика Мухаммеда ибн Муса аль-Хорезми (Alhorithmi), жившего в 783—850 гг. В своей книге "Об индийском счете" он изложил правила записи натуральных чисел с помощью арабских цифр и правила действий над ними "столбиком", знакомые теперь каждому школьнику. В XII веке эта книга была переведена на латынь и получила широкое распространение в Европе.

В течение длительного времени термин «алгоритм» употребляли преимущественно математики. При этом они пользовались так называемым интуитивным понятием алгоритма - заранее заданное, понятное и точное предписание возможному исполнителю совершить определенную последовательность действий для получения решения задачи за конечное число шагов.[1]

Решая различные задачи, математики столкнулись с рядом неразрешимых проблем, т.е. задач, для которых не удавалось создать решающий их алгоритм. Это стало предпосылкой к обоснованию сущности алгоритмов формальным, т.е. математическим путём.

Основные результаты теории алгоритмов были получены в 30-60 годах 20 века Э.Черчем, А. Тьюрингом, А. Постом, А. Колмогоровым, А. Марковым. Введенные в рассмотренные алгоритмические модели, машины Тьюринга, Поста дали возможность устанавливать алгоритмическую разрешимость проблемы путём построения соответствующих машин логического действия.

В настоящее время понятие алгоритма является не только одним из главных понятий математики, но одним из главных понятий современной науки. Более того, с наступлением эры информатики алгоритмы становятся одним из важнейших факторов цивилизации. [1]

Определение 1.Алгоритм – конечная последовательность детерминированных арифметических и логических действий над исходными и промежуточными данными задачи обработки информации, выполнение которых приводит к правильному ее решению, т.е. получению требуемых выходных данных. [2]

Свойства алгоритмов.

1. Понятность. Исполнитель алгоритма должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный вариант исходных данных, исполнитель должен знать, как надо действовать для выполнения этого алгоритма.

2. Дискретность (прерывность, раздельность). Алгоритм должен состоять из отдельных элементарных шагов. Количество шагов должно быть конечным, т.е. после выполнения этих шагов исполнитель должен остановиться. Если действия повторяются бесконечно, говорят, что алгоритм зациклился.

3. Определённость. Последовательность шагов алгоритма должна быть детерминированной (определённой). После каждого шага либо указывается, какой шаг выполнить дальше, либо даётся команда остановки, после этого действия алгоритма считаются законченными.

4. Результативность (конечность). После выполнения конечного количества шагов алгоритм должен выдавать правильный результат решения той или иной информационной задачи.

5. Массовость. Алгоритм решения задачи должен разрабатываться в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, так называемой области применимости алгоритма.[2]

Способы представления алгоритмов.

1. Графический (в виде блок-схемы).

2. Словесный, текстовый (в виде последовательности шагов, описывающих действия естественным языком).

3. Программный (в виде программы, полностью или сжато представленной на каком-либо алгоритмическом языке).

Наиболее наглядным считается графический способ. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

Таблица 1 – Символы блок-схем алгоритмов

Процесс		Выполнение операций или групп операций, в результате которых изменяется значения, форма представления или расположение данных.
Решение		Выбор направления выполнения алгоритма или программы в зависимости от некоторых переменных условий
Модификация		Выполнение операций, меняющих команды ил группу команд, т.е. изменяющий программу
Предопределенный процесс		Использование ранее созданных и отдельно описанных алгоритмов и программ
Ручной ввод		Ввод данных оператором в процессе обработки при помощи устройства, непосредственно сопряжённого с вычислительной машиной
Дисплей		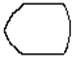Ввод-вывод данных в случае, если непосредственно подключенное к процессору устройство воспроизводит данные и позволяет оператору вносить изменения в процессе их обработки
Документ		Ввод-вывод данных, носителем которых служит бумага.

Линия потока		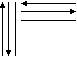Указание последовательности связей между символами
Соединитель		Указание связи между прерванными линиями потока, связывающими символы
Пуск-остановка		Начало, конец, прерывание процесса обработки данных или выполнения программы
Комментарий		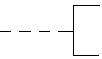Связь между элементом схемы и пояснением
Межстраничный соединитель		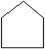Указание связи между разъединительными частями схем алгоритмов и программ, расположенных на разных листах.

Продолжение таблицы 1

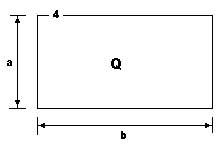
Размеры символов должны удовлетворять соотношению b=1,5a, рис. 1. На этом же рисунке продемонстрирован пример использования символа «комментарий».

Функции спроса на автомобиль Q = 0.3882-0.23*P

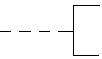
Рис. 1 Фрагмент блок-схемы алгоритма

Таблица 2 – Унифицированные структуры

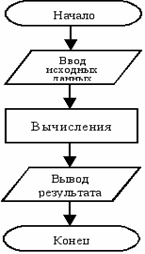	Следование
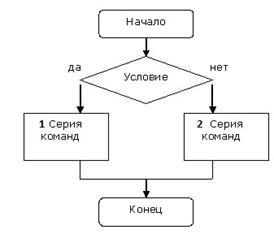	Полное ветвление
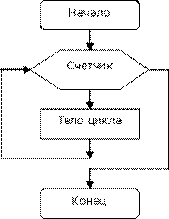	Цикл с параметром

Продолжение таблицы 2

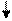
Тело цикла	Цикл с предусловием
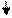
Тело цикла	Цикл с постусловием

В зависимости от употребляемых унифицированных структур алгоритмы программных модулей, составляющих программный комплекс, могут быть линейными, разветвляющимися, циклическими и сложными.

Этапы решения задач на ЭВМ.

1. Постановка задачи

2. Анализ и исследование задачи, модели

3. Разработка алгоритма

4. Программирование

5. Тестирование и отладка

6. Анализ результатов решения задачи и уточнение в случае необходимости математической модели с повторным выполнением этапов 2-5

7. Сопровождение программы

В данном учебном пособии на примерах решения конкретных задач рассматриваются этапы решения на ЭВМ с первого по четвертый. На практических занятиях при выполнении заданий необходимо представить этапы решения с первого по шестой. Для иллюстрации этапов решения задач на ЭВМ (1-3) рассмотрим следующую задачу.

Задача 1.

1. Составить алгоритм приближенного вычисления квадратного корня 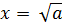с заданной точностью 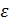методом Ньютона.

2. Очередное значение корня 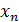вычисляется по формуле 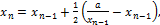n=1, 2, …при условии, что задано начальное значение корня 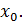Первое значение корня будет равно 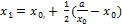, второе – 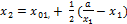и т.д. Корень можно считать вычисленным с заданной точностью 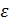, если модуль очередного уточнения корня | .

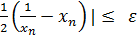3. Блок-схема алгоритма на рис. 2.

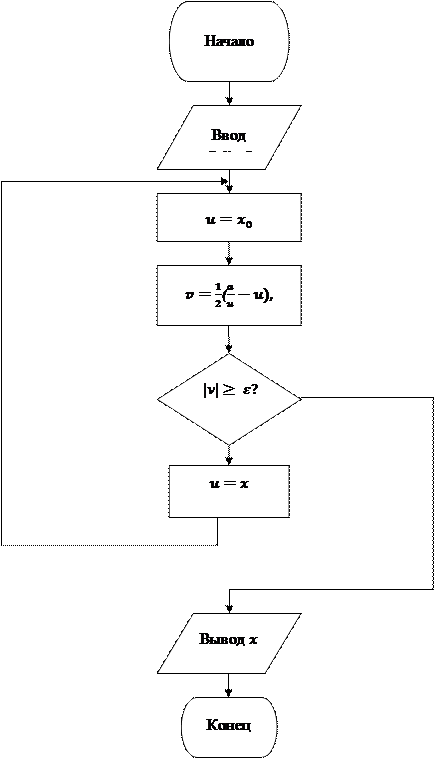
Рис. 2 Алгоритм вычисления квадратного корня методом Ньютона.

ЛИНЕЙНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ АЛГОРИТМЫ

Определение 2. Линейный алгоритм – это алгоритм, содержащий алгоритмическую структуру «следование.

Общий вид блок-схемы линейного алгоритма представлен в таблице 2. Рассмотрим 1-3 этапы решения задачи на ЭВМ с помощью линейного алгоритма.[2]

Задача 2.

1. Даны два действительных положительных числа a и b. Найти среднее арифметическое и среднее геометрическое этих чисел.

2. Среднее арифметическое чисел a и b определяется как
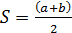, а среднее геометрическое как .

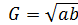3. Блок-схема алгоритма представлена на рис.3.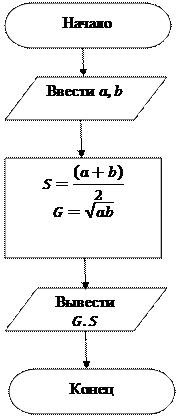

Рис. 3 Алгоритм вычисления среднего арифметического и среднего геометрического двух чисел.