Основные вычислительные алгоритмы

Алгоритмические (или вычислительные) процессы обработки данных делятся на виды:

- линейные,

- ветвящиеся,

- циклические.

Линейным называется такой вычислительный процесс, в котором самостоятельные этапы вычислений выполняются в последовательности их записи, т.е. в естественном порядке.

Каждая операция является самостоятельной, независимой от каких-либо условий.

Линейные вычислительные процессы имеют место при вычислении арифметических выражений.

Пример 1:

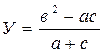
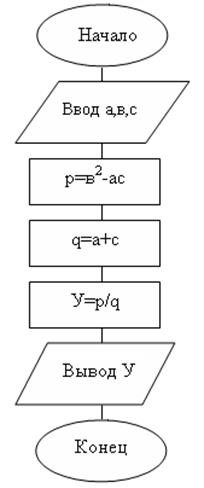
Ветвящимсяназывается такой процесс, в котором его реализация происходит по одному из нескольких заранее предусмотренных (возможных) направлений в зависимости от исходных условий или промежуточных результатов. Каждое отдельное направление вычислений в таком процессе называется ветвью вычисления. Выбор осуществляется проверкой выполнения логического условия.

В каждом конкретном случае обработки данных вычислительный процесс выполняется лишь по одной ветви, а выполнение остальных – исключается.

Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей- сложным. Сложный ветвящийся процесс можно представить с помощью простых ветвящихся процессов.

Направления ветвления выбирается логической проверкой, в результате которой возможны два ответа: «да» - условие выполнено, «нет» -условие не выполнено.

Любая ветвь, по которой осуществляются вычисления, должна приводить к завершению вычислительного процесса.

Пример 2:

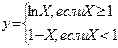
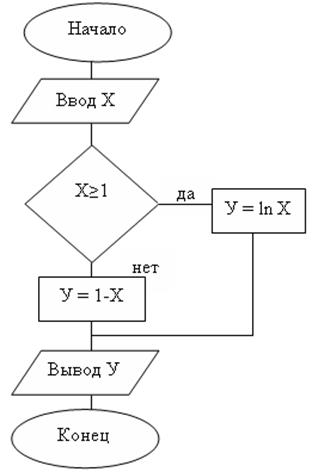
При реализации алгоритмов многих задач наблюдается многократное повторение отдельных этапов их вычислительного процесса. Такие многократно повторяемые этапы вычислений называются циклами, а вычислительные процессы, содержащие многократно повторяемые этапы называются циклическими.

Пример 3:

У=X²⁰

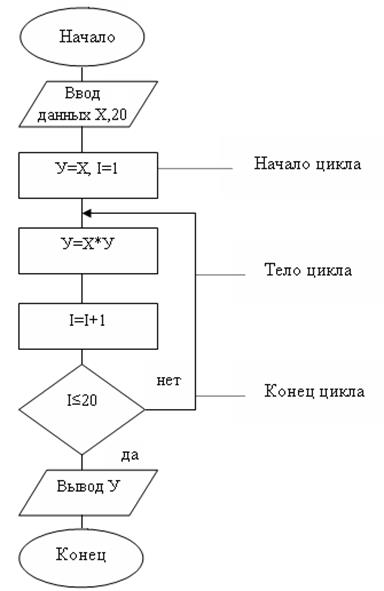
Анализ алгоритмов

Целью анализа трудоемкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.

Трудоёмкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоёмкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.