Информационное скрытие при активном противодействии нарушителя

В рамках первого подхода к оценке СПС, рассмотрим общую формулировку задачи информационного скрытия в случае активного противодействия со стороны нарушителя. Основные результаты этого подхода были получены в работе [61] и применены в [5]. Рассмотрим некоторые их них.

Формулировка задачи информационного скрытия при активном противодействии нарушителя

Рассмотрим обобщенную структурную схему стеганографической системы передачи скрытых сообщений, представленную на рис. 4.1.

Рис. 4.1. Обобщенная структурная схема стеганосистемы при активном противодействии нарушителя

В этой схеме скрываемые сообщения m равномерно распределены во множестве сообщений М и должны быть безошибочно переданы декодеру. Передающая сторона подает пустой контейнер с^N (который представляет собой последовательность с N независимо и идентично распределенных отсчетов в соответствии с распределением контейнера р(с) ), секретный ключ kⁿ (каждый символ k_i ( которого независимо и равномерно распределен по функции р(k)), и сообщения m на вход кодера. Последний формирует cтеганограмму s^N которая передается получателю по незащищенному каналу связи.

Стеганограмма s^N перехватывается и обрабатывается нарушителем с целью разрушения или удаления сообщения m. Искаженную нарушителем стеганограмму пометим как , а атакующее воздействие — условной функцией распределения

Эта обработка включает, как частный случай формирование искаженной стега-нограммы в виде

где q — детерминированное изображение.

Основное предположение: нарушитель знает распределение всех изменений в стеганосистеме и, собственно, описание стеганосистемы, но не знает используемого секретного ключа (принцип Керхгофса для систем зашиты информации).

Пусть контейнер с, стеганограмма s и модифицированная нарушителем стега-нограмма 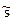принадлежат одному множеству . Декодер получателя вычисляет оценку первичного скрытого сообщения m. Если 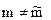, то атакующий сумел разрушить информацию, которая защищалась стеганографической системой.

Формально определим внесенные искажения в стратегиях передающей стороны и нарушителя. Это завершает математическое описание стеганосистемы и позволяет определить скорость безошибочной передачи для схемы, представленной на рис. 4.1.

Определение 4.1

Функция искажения, вносимого отправителем сообщения, представляет собой неотрицательную функцию

Определение 4.2

Функция искажения вносимого атакующей стороной, представляет собой неотрицательную функцию

Функция искажения d₁-ограничена:

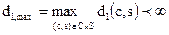
Кроме того, данная мера искажения симметрична 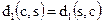для всех . Выполнение равенства означает совпадение: с=s. Если 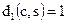, то контейнер-результат не соответствует контейнеру-оригиналу.

Функции искажения 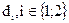распространяются на искажения символьных последовательностей с длиной блоков N:

Назовем искажение контейнера с, вызванное встраиванием в него скрытого сообщения m, искажением, вызванным кодированием, а искажение, вызванное атакующими действиями нарушителя, — искажением, вызванным атакующим воздействием.

Стеганосистема с длиной блоки N, приводящая к искажению, вызванному кодированием, уровень которого не превышает А₁ является совокупностью множеств скрываемых сообщений М с количеством элементов (мощностью) |M| контейнеров С, стеганограмм 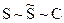и ключей К, а также определенных на них функций кодирования Е и декодирования D. При этом Е — отображение контейнера с^N, сообщения m и ключа k^N в стеганограмму:

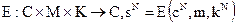
Это отображение ограничено величиной среднего искажения А₁, вызванного кодированием:

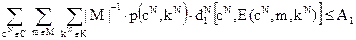(4.1)

Отображение 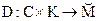— декодирующее отображение принятой стеганопоследовательности и ключа k^N в декодированное сообщения

Таким образом, величина А₁ характеризует максимально допустимую степень искажения контейнера при встраивании в него скрываемого сообщения. Несмотря на то, что данное определение формально описывает стеганосистемы блочного типа, на практике оно может быть расширено и на стеганосистемы потокового типа, в которых окно обработки описывается скользящим блоком длиной N. В этом случае параметр N стеганосистемы может быть назван длиной кодового ограничения стеганосистемы (по аналогии с непрерывными кодами).

В большинстве случаев искажение А₁ является малым, поскольку априорно принимается, что результат встраивания в контейнер сообщения должен быть незаметным для постороннего лица (в том числе и нарушителя). В стеганосистемах, в которых контейнер представляет собой полезный для получателя информационный сигнал и качество которого необходимо сохранить, величина А₁ ограничивается. В системах ЦВЗ требование минимизации А₁ формулируется как требование прозрачности водяного знака, свидетельствующего о принадлежности контейнера [5].

Кроме того, определение ограничения искажения (4.1) содержит усреднение по отношению к распределению 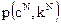и по отношению к равномерному распределению сообщений. Такой выбор сделан для удобства, поскольку это позволяет использовать классические положения теории Шеннона [60].

Распределение 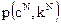и выбор отображения Е определяют конкретный вид распределения множеств формируемых стеганограмм.

Определение 4.4

Атакующее воздействие (без памяти), приводящее к искажению А₂, описываетсяусловной функцией распределения из множества S к множеству 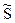, такой, что выполняется условие

(4.2)

По определению, А₂ является максимальной величиной искажения стеганограммы, вызванного умышленными действиями нарушителя. Физический смысл ограничения величины А₂ заключается в следующем. В системах ЦВЗ нарушитель, пытаясь удалить водяной знак из заверенного контейнера, вынужден сам уменьшать величину А₂, чтобы существенно не исказить ценный для него контейнер. В других стеганосистемах величина А₂ ограничивается имеющимся у атакующего энергетическим потенциалом установления помех, возникающими помехами для других каналов связи при использовании общего ресурса и другими причинами.

Логично предположить, что для реальных стеганосистем обычно выполняется соотношение 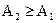[5].

В соответствии с определением 4.4, атакующее воздействие описывается и ограничивается усредненными искажениями между множествами S и . В других случаях, если атакующий знает описание функции E, то атакующее воздействие описывается и ограничивается усредненным искажением между множествами С и :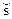

(4.3)

Определение А₂ в соответствии с выражением (4.3) допускает, что нарушителю известны точные вероятностные характеристики контейнеров. Как будет показано дальше, это обстоятельство существенно усложняет задачу обеспечения защищенности скрываемой информации, поэтому в устойчивых стеганосистемах используются разные методы скрытия от нарушителя характеристик используемых контейнеров. Например, такие методы включают использование для встраивания подмножества контейнеров с вероятностными характеристиками, отличающимися от характеристик всего множества известных нарушителю контейнеров, или рандомизированную компрессию сигнала контейнера перед встраиванием в него скрываемого сообщения [15]. Поэтому вычисление искажения А₂ в соответствии с определением (4.4) является более универсальным, поскольку нарушитель всегда имеет возможность изучать вероятностные характеристики наблюдаемых стеганограмм.

Имея описание стеганосистемы и атакующего воздействия , можно описать состязание (игру) между передающей и атакующей сторонами.

Определение 4.5

Информационно-скрывающее состязание, которое приводит к искажениям (А₁, А₂), описывается взаимосвязью используемой стеганосистемы, вызывающей искажение кодирования А₁, к атакующего воздействия, вызывающего искажение А₂ Скорость передачи скрытых сообщений по стеганоканалу определяется в виде . При этом скорость передачи R выражается через среднее количество бит скрываемого сообщения, которые безошибочно передаются (переносятся) одним символом (пикселем, отсчетом) стеганопоследовательности s^N .

Это определение созвучно "классическому" определению скорости передачи обычных сообщений по каналу открытой связи, которая выражается в среднем количестве безошибочно переданных бит за одно использование канала [60,65,70].

Вероятность разрушения скрытого сообщения (среднюю вероятность ошибки) в стеганопоследовательности длиной N определяют как

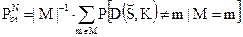
(4.4)

где скрываемые сообщения m равномерно выбираются из множества М. Вероятность 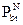является усредненной на множестве всех сообщений вероятностью того, что атакующий успешно исказит скрыто передаваемое сообщение. Атакующий достигает успеха в информационном состязании, если декодированное во время приема сообщение не совпадает со встроенным в контейнер скрываемым сообщением, или же декодер неспособен принять однозначное решение.

Теоретически достижимую скорость безошибочной передачи скрываемых сообщений и скрытую пропускную способность при. искажениях не более, чем (А₁, А₂), предлагается определить следующим образом.

Определение 4.6

Скорость R безошибочной передачи скрываемых сообщений является достижимой для искажений не более, чем (А₁, А₂), если существует стеганосистема с длиной блока N, которая приводит к искажению кодирования не более А₁ на скорости 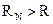, такая что 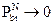при 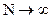при любых атаках нарушителя, приводящих к искажениям не более А₂.

Определение 4.7

Скрытая пропускная способность В(А₁, А₂) является супремумом (верхним пределом) всех достижимых скоростей безошибочной передачи скрываемых сообщений при искажениях не более (А₁, А₂).

Таким образом, СПС является верхним пределом скорости безошибочной передачи скрываемых данных, при которой искажения контейнера, вызванные встраиванием в него указанных сообщений (А₁) и действиями нарушителя по разрушению этих сообщений (А₂), не превышают заданных величин.

Как и ПС каналов передачи открытых сообщений, ПС каналов передачи скрываемых сообщений определяется в идеализированных условиях, при которых задержка кодирования/декодирования бесконечна (то есть 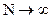), статистика контейнеров, скрываемых сообщений, стеганограмм и ключей точно известна, сложность построения стеганосистемы не ограничена.

Совершенно очевидно, что такая пропускная способность канала скрытой связи имеет смысл теоретического предела, указывающего области, в которых существуют и, соответственно, не существуют стеганосистемы при заданных величинах искажений. Известно, что скорости реальных систем передачи открытых сообщений могут только приближаться к величине ПС открытых каналов, причем по мере приближения к ней вычислительная сложность реализации систем передачи возрастает сначала приблизительно по линейной, а затем — по квадратичной и далее по экспоненциальной зависимости от длины блока кодирования N [60].

Вполне вероятно, что аналогичные зависимости возрастания сложности справедливы и для стеганосистем в меру приближения скорости передачи скрываемых данных к величине СПС. Это предположение подтверждается имеющимся опытом построения стеганосистем [5]. Известно, что попытки увеличить скорость передачи скрываемых данных приводят к существенному усложнению методов скрытия информации [63, 66].

Скрывающее преобразование

Для полного представления стеганосистемы и условий ее функционирования представим формальное описание скрывающего преобразования, выполняемого при встраивании информации в контейнер, и атакующего влияния, осуществляемого нарушителем для противодействия скрытой передаче. Для этого рассмотрим вспомогательную случайную последовательность и, определенную на множестве U.

Физически последовательность u описывает результат преобразования скрываемого сообщения m с целью его адаптации к встраиванию в контейнер заданного формата. Следует отметить, что в то время как в стеганосистеме ключи и стеганограммы представляют собой последовательности одинаковой длины N, длина скрываемых сообщений, их алфавит и вероятностное распределение в преобладающем большинстве случаев не совпадают с соответствующими характеристиками указанных последовательностей.

Определим вспомогательное множество

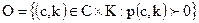
Тогда мощность множеств U должна удовлетворять условию:

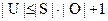
В общем виде скрывающее преобразование, используемое отправителем для встраивания скрываемого сообщения в контейнер, определяется следующим образом.

Определение 4.8

Скрывающее преобразование, вызывающее искажение кодирования A₁ описывается условной функцией распределения отображения из множества в множество , такой, что выполняется условие

(4.5)

Расширение скрывающего преобразования без памяти длиной N описывается следующей условной функцией:

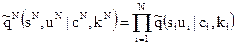(4.6)

Для успешного скрытия информации от квалифицированного нарушителя целесообразно использовать не одно, а множество скрывающих преобразований сообщений.

Определение 4.9

Обобщенное скрывающее преобразование, приводящее к искажению кодирования не более величины A₁ состоит из множества 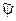всех скрывающих преобразований, удовлетворяющих условию (4.5).

Обобщенное скрывающее преобразование описывает все возможные варианты действий отправителя при встраивании сообщений m в контейнер таким образом, чтобы величина искажения кодирования не превышала допустимую A₁. Следует отметить, что в стеганографии важно, чтобы у скрывающего информацию существовало множество возможных вариантов, среди которых он равновероятно и непредвиденно для нарушителя выбирает конкретный вариант скрытия сообщения, требующего защиты.

Для анализа стеганосистемы удобно записать функцию 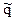в форме произведения функций распределения:

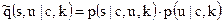(4.7)

где 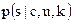относится к "основному" скрывающему преобразованию, 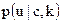— к "вспомогательному" скрывающему преобразованию.

Атакующее воздействие

Рассмотрим формальное описание действий нарушителя относительно преобразования перехваченной стеганограммы s в искаженную стеганограмму 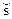с целью разрушения содержащейся в ней скрытой информации.

Определение 4.10

Атакующее воздействие, вызывающее искажение A₂ описывается условной функцией распределения q(s\s) отображения из множества S в множество S, такой, что выполняется условие

(4.8).

Расширение атакующего воздействия без памяти длиной N описывается условной функцией вида

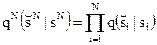(4.9).

Определение 4.11

Обобщенное атакующее воздействие, вызывающее искажение не более величины A₂, состоит из множества у всех атакующих воздействий, которые удовлетворяют условию (4.8).

Аналогично набору вариантов действий передающей стороны, у атакующего также есть свой набор атакующих воздействий (множество ). Нарушитель, перехватив стеганограмму, пытается выбрать такое атакующее воздействие из множества , которое максимизировало бы вероятность разрушения скрытой в ней информации.