Решение задачи в среде MathCAD

Содержание

Введение. 5

1 Адаптивные системы.. 6

2 Решение задачи в среде MathCAD.. 8

3 Решение задачи в MS Office Excel 15

Список использованных источников. 20

Приложение А (обязательное) Разработка комплексного документа средствами интегрированного покета MS Office. 21

Введение

При выполнении данного курсового проекта будет произведен спектральный анализ и восстановление периодического сигнала при помощи программных сред MathCAD и MS Excel, разработан комплексный документ средствами интегрированного пакета Microsoft Office.

Адаптивные системы

Системы, автоматически изменяющие значение своих параметров или структуру при непредвиденных изменениях внешних условий на основании анализа состояния или поведения системы так, чтобы сохранялось заданное качество ее работы, называют адаптивными системами. Адаптивные системы с изменением значений параметров иногда называют самонастраивающимися, а системы с изменением структуры – самоорганизующимися.

Обычно адаптивная система содержит в качестве «ядра» схему, реализующую один из фундаментальных принципов управления, а контур адаптации пристраивают к ней как вторичный, осуществляющий коррекцию параметров. Контур адаптации, обычно состоящий из устройства измерения (ИУ), вычисления (ВУ) и управления (УУ), может быть разомкнут (рисунок 1), если на его вход подается только входное воздействие, или замкнут (связь показана пунктиром), если он реагирует также и на выходную координату системы. Основной контур составляет объект О и регулятор Р.

Рисунок 1 – Адаптивная САУ

Контур самонастройки воздействует на блок настройки параметров БНП, который может быть включен не только последовательно, как показано на рисунке, но и любым другим способом, например, в цепь обратной связи. Вычисление воздействий для коррекции параметров осуществляет ВУ в соответствии с программой.

Классификация САУ по другим признакам имеет более общий характер и слабо связана с фундаментальными принципами управления.

В зависимости от принадлежности источника энергии, при помощи которого создается управляющее воздействие, САУ могут быть прямого и непрямого действия. В системах прямого действия используется энергия управляемого объекта. В системах непрямого действия управляющее воздействие создается за счет энергии дополнительного источника.

По виду сигналов, действующих в системах, последние разделяют на непрерывные и дискретные. Дискретные системы, в свою очередь, разделяются на импульсные, релейные и цифровые.

САУ, у которых управляемая величина в установившемся режиме зависит от величины возмущающего воздействия, называются статическими, а САУ, у которых управляемая величина не зависит от возмущения, называются астатическими.

Решение задачи в среде MathCAD

Временная диаграмма сигнала представлена на рисунке 2. Параметры импульсной последовательности: амплитуда импульса U_m = 10 В; длительность импульса τ_u = 0,1 мс; период повторения импульсов T_n = 1 мс.

Рисунок 2 – Временная диаграмма сигнала

Во временной области математическая модель сигнала имеет вид:

(1)

Чтобы графически представить амплитудно-частотный спектр (АЧС) сигнала, необходимо вычислить амплитуды гармоник (колебаний синусоидальной формы), определяющих форму сигнала u(t). Амплитуды гармоник U_k (где k – номера гармоник, k = 1,2, …, n), находят по формуле

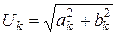, (2)

где коэффициенты ряда Фурье a_k и b_k определяют из выражений

, (3)

. (4)

Постоянную составляющую (среднее значение напряжения за период) находят из выражения

. (5)

Поскольку заданный сигнал u(t) существует только на временном интервале t ϵ [0, τ_u], то в приведенных формулах (3), (4) и (5) нижний и верхний пределы интегрирования принимаем равными значениями переменной t в начале и в конце указанного интервала. Частота первой гармоники ω₁ определяется из выражения

. (6)

Для построения фазочастотного спектра начальные фазы k-x гармоник определяют по формуле

, (7)

если коэффициенты b_k > 0, в противном случае используют формулу

. (8)

Числовые значения коэффициентов a_k и b_k в формулы (7) и (8) подставляют с учетом их знаков.

Формулы (7) и (8) используют для расчета начальных фаз гармоник, если при восстановлении исходного сигнала по известному спектру применяют синусную форму записи ряда Фурье для бесконечной во времени периодической функции, то есть выражение

. (9)

Если же ряд Фурье записывают в косинусной форме

, (10)

то начальные фазы гармоник находят по формулам

, (11)

или

. (12)

Для построения временной диаграммы сигнала в системе MathCAD используют программу вычислений в цикле. Фрагменты программ построения диаграммы исходного сигнала, его амплитудно-частотного и фазочастотного спектров в системе MathCAD показаны на рисунках 3, 4 и 5 соответственно.

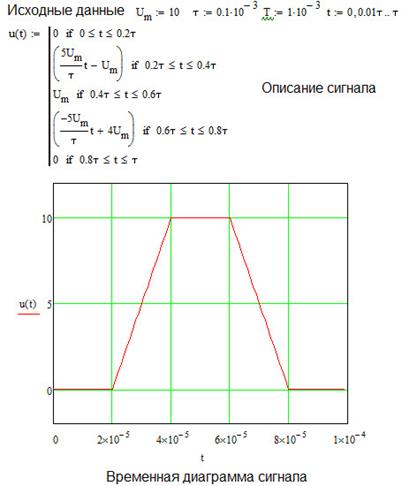
Рисунок 3 – Построение временной диаграммы сигнала

Рисунок 4 – Построение амплитудно-частотного спектра

Рисунок 5 – Построение фазочастотного спектра

Фрагмент программы восстановления исходного сигнала в системе MathCAD показан на рисунке 6.

Рисунок 6 – Восстановление сигнала во временной области по заданному спектру

Как видно из рисунка 6, при использовании числа членов ряда Фурье (числа гармоник) N = 100 временная диаграмма восстановленного сигнала отличается от временной диаграммы исходного сигнала незначительно. Для полного воспроизведения формы сигнала число гармоник должно стремиться к бесконечности, что возможно только теоретически.

На рисунке 7 в виде таблицы представлены результаты вычисления постоянной составляющей и амплитуд первых десяти гармоник U_k спектра исследуемого сигнала. Данные приведены для проведения сравнительного анализа результатов решения задачи в среде MathCAD и Excel.

Рисунок 7 – Результаты расчета в MathCAD