Расчет надежности систем с функциональным резервированием

В настоящее время широко распространяется функциональное ре­зервирование. Типичным примером такого резервирования являются од­нородные реконфигурируемые системы, когда одна и та же ячейка может в разные моменты времени выполнять разные функции. Очевидно, что здесь понятие резервируемого блока и резервного блока напрямую не приме­нимы. Как правило, для расчета таких систем наряду с теорией надежности используется теория массового обслуживания, т.е. следует проводить рас­чет надежности невосстанавливаемых СМО, состоящий из ненадежных элементов с ограниченным резервом.

Рассмотрим расчет такой системы на примере однородной реконфи­гурируемой системы измерительных преобразователей (ОРС ИП), которая является типичной для АСУ ТП, а также в трактах телеизмерения в составе многофункциональных систем телемеханики. Сформулируем понятие от­каза для данной системы.

Изначально предположим, что ячейки системы абсолютно надежны, т.е. в течение заданного времени не выходят из строя. Пусть имеется ОРС ИП с числом ячеек k, из которых при необходимости можно сформировать до n измерительных преобразователей. При поступлении заявки на обслу­живание устройство управления ОРС ИП формирует из числа свободных ячеек измерительный преобразователь требуемой точности, т.е. один ка­нал обслуживания. Если свободных ячеек недостаточно, имеет место отказ в обслуживании заявки [2].

Однако в общем случае ячейки ОРС ИП не являются абсолютно на­дежными и со временем могут выходить из строя. При этом отказавшая ячейка не восстанавливается до отказа всей системы. Учитывая это обстоя­тельство, в ОРС ИП следует предусмотреть в дополнение к k исходных ячеек определенное количество резервных ячеек так, чтобы в течение за­данного времени работы число функционирующих ячеек не опускалось ниже k.

Сформулируем понятие отказа для модифицированной модели сис­темы. Отказ системы – это ситуация, когда при приходе заявки на обслу­живание новый канал не может быть сформирован, т.е. заявка не обслужи­вается либо из-за недостаточного количества изначально запланированных ячеек (включая резервные), либо из-за уменьшения количества свободных ячеек в результате их выхода из строя.

Поставим задачу следующим образом: следует рассчитать w –коли­чество ячеек однородной реконфигурируемой системы, состоящее из k – числа основных ячеек (позволяющих сформировать n каналов обслужива­ния) и r – числа дополнительных ячеек, чтобы за заданное время t_зад отказ системы наступил с вероятностью не больше чем Q_зад.

Решение задачи можно разделить на два этапа. На первом этапе сле­дует рассчитать количество ячеек k ОРС ИП, обеспечивающее заданную вероятность отказа в обслуживании, предполагая идеальную надежность ячеек. На втором этапе (зная уже число основных ячеек k) необходимо рас­считать число дополнительных ячеек r, обеспечивающее заданную вероят­ность отказа в обслуживании, предполагая, что ячейки ненадежны.

В соответствии с данным подходом при функционировании ОРС ИП имеют место два независимых события. Первое событие заключается в том, что k ячеек не хватило для формирования n каналов – это отказ иде­ального преобразователя (вероятность данного события Q_обс). Расчет веро­ятности этого события ведется с помощью методов теории массового об­служивания. Второе событие заключается в том, что за заданное время вышло из строя более r ячеек – это недостаточность заложенного в сис­тему резерва (вероятность данного события Q_яч). Расчет вероятности вто­рого события ведется с помощью методов теории надежности.

Отказ системы (в несколько упрощенной формулировке, позволяю­щей значительно уменьшить объем вычислений) заключается в том, что произошло либо первое событие, либо второе, и, таким образом, представ­ляет собой сумму двух вышеуказанных независимых событий. Следова­тельно, его вероятность равна сумме вероятностей этих событий:

Q_зад = Q_обс + Q_яч. (2.82)

В первом приближении и поток заявок, и поток выхода из строя ячеек можно считать пуассоновскими. Пуассоновский поток обладает сле­дующими свойствами: а) стационарностью, т.е. его характеристики не ме­няются во времени; б) отсутствием последействия, т.е. интервал до насту­пления следующего события не зависит от предыдущего; в) ординарно­стью, т.е. два события одновременно произойти не могут.

Обозначим через l плотность потока, т.е. среднее число событий, приходящееся на единицу времени. Вероятность того, что за время tпро­изойдет ровно m событий,

. (2.83)

На первом этапе, как уже говорилось, рассчитывается k – число ячеек ОРС ИП, в предположении об идеальной надежности ячеек.

Рассмотрим процесс обслуживания заявок ОРС ИП. Этот процесс является марковским, т.е. для каждого момента времени вероятность лю­бого состояния системы в будущем зависит только от состояния системы в настоящий момент и не зависит от того, каким образом система пришла в это состояние [1]. Пусть для данной системы l – плотность потока заявок, а m – плотность потока освобождений. Введем понятие приведенной плот­но­сти потока заявокa, где

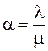. (2.84)

Тогда, в соответствии с формулой Эрланга,

, (2.85)

где n – количество каналов обслуживания системы.

Q_обс выбирается на основе формулы (2.82) в каждом случае по своим конкретным соображениям, в зависимости от того, что важнее – повысить вероятность обслуживания идеального преобразователя или повысить ве­роятность того, что заложенного в систему резерва окажется достаточно.

Таким образом, зная плотности потока заявок и потока освобожде­ний и задавшись Q_обс, можно рассчитать n. Если считать, что в среднем на формирование канала требуется a ячеек, то требуемое число ячеек идеаль­ной ОРС ИП

k = an. (2.86)

На втором этапе рассчитывается r – число резервных ячеек ОРС ИП, в предположении того, что ячейки ненадежны. Методика расчета является многошаговой и основана на переборе.

Вероятность того, что за заданное время выйдет из строя не более r ячеек с учетом формулы (2.82)

P_яч = 1–Q_яч=1– (Q_зад – Q_обс). (2.87)

Для пуассоновского потока вероятность того, что число отказов за время t_зад будет не больше r,

(2.88)

Методом перебора находим такое количество резервных ячеек r, при котором вероятность выхода всех резервных ячеек из строя меньше задан­ной.

Проиллюстрируем данную методику примером. Пусть требуется оп­ределить количество ячеек w при следующих исходных данных: плот­ность потока заявок l = 100 1/с, плотность потока освобождений m = = 50 1/с, среднее количество ячеек на канал a = 10, вероятность отказа сис­темы Q_зад = 0,001, интенсивность отказов ячейки и связанной с ней ком­мутационной аппаратуры l_яч = 10^–4 1/с, заданное время t_зад = 1000 ч.

В соответствии с алгоритмом определяем, что для нас важнее: повы­сить вероятность обслуживания идеального преобразователя или повы­сить вероятность того, что заложенного в систему резерва окажется доста­точно. Предположим, обе вероятности важны одинаково. Тогда Q_обс = Q_яч.= = Q_зад/2 = 0,0005 и, соответственно формуле (2.87), P_яч = 0,9995.

На первом этапе рассчитывается число ячеек ОРС ИП, состоящей из абсолютно надежных элементов. По формуле (2.85) подбираем нужное ко­личество каналов

n = 7.

Тогда требуемое количество ячеек без учета вышедших из строя в соответствии с формулой (2.86)

k = an = 70.

На втором этапе рассчитывается число резервных ячеек r ОРС ИП, состоящей из ненадежных элементов.

Интенсивность отказов системы λ_Σв предположении об экспоненци­альном распределении наработки на отказ равно сумме интенсивностей отказов элементов системы:

λ_Σ = λw = λ(k + r). (2.89)

Предположим, что в систему не добавлено ни одного резервного элемента, т.е. r = 0.

При r = 0

. (2.90)

Вероятность того, что на заданном интервале времени не выйдет из строя ни одна ячейка, значительно меньше заданной. Начинаем добавлять резервные элементы:

при r = 1

; (2.91)

при r = 2

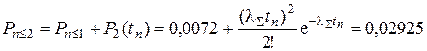; (2.92)

при r = 3

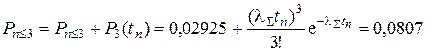(2.93)

и т.д., пока при r = 19 , т.е. вероятность того, что в сис­теме на заданном интервале времени число ячеек не опустится ниже k, превысит заданную.

Таким образом,

w = k + r = 70 + 19 = 89.

Следовательно, в соответствии с разработанным алгоритмом преоб­разователь должен в начальной стадии содержать 89 исправных ячеек.

Данная система, безусловно, не охватывает все стороны функцио­нального резервирования, однако является достаточно типичной, чтобы приведенная методика расчета могла быть принята за базовую.