Определение расчетного сопротивления грунта основания для песков

КОНТРОЛЬНАЯ РАБОТА №2

По механике грунтов

Выполнил: студент 3 курса Кокульев В.Н.

шифр: 208914 ПГС «с»

Проверил: Буслов А.С.

г. Москва, 2012

Содержание курсовой работы

1. Построение эпюры вертикальных нормальных напряжений………..…… 3

2. Определение вертикальных нормальных напряжений от собственного веса грунта …………………………………………………………………………… 7

3. Определение расчетного сопротивления грунта основания

для песков…………………………………………………………………...........9

4. Определение расчетного сопротивления глинистых грунтов…................ 13

5. Расчет осадок фундаментов ……………………………………..…..……. 17

Список используемой литературы …………………………………….……... 19

Построение эпюры вертикальных нормальных напряжений

Теория

При нагрузке, равномерно распределенной по прямоугольной площадке 2l₁х2b₁, вертикальные нормальные напряжения по вертикали, проходящей через центр этой площадки,

σ		=	2p		arctg	η	+	ζη(1+η2+2ζ2)		(1)
z	π	ζ√1+ζ2+η2	(ζ2+η2) (1+ζ2)√1+ζ2+η2

а через угловую точку площадки

σ	с	=	p		arctg	η	+	ζ1η(1+η2+2ζ12)		(2)
z	2π	ζ1√1+ζ12+η2	(ζ12+η2)(1+ζ12)√1+ζ12+η2

где η=l₁/b₁=l/b, ζ=z/b₁=2z/b и ζ ₁= z/(2b₁)= z/b

Из сопоставления формул (1) и (2) следует, что

σ	с	=		σ			(3)
z		z/2	,

т.е. вертикальное нормальное напряжение на глубине z под углом (corner) равномерно загруженной прямоугольной площадки в 4 раза меньше соответствующего напряжения на глубине z/2 под центром этой площадки

Для удобства пользования формулы (1) и (2) могут быть представлены в виде:

σ	o	=	p	α			(4)
z
σ	с	=	p	α	/4		(5)
z

Где α -коэффициент (табл. 1), зависящий от η и ζ для σ_z⁰

и от η и ζ₁ для σ_z^c.

Табл. 1. Значения коэффициента α в формуле (4)

ξ= 2z/b	Для круглых фундаментов	Для прямоугольных фундаментов с отношением сторон η=l/b:	Для ленточных фундаментов при n > 10
	1,2	1,4	1,6	1,8		2,4	2,8	3,2
0,0 0,4 0,8 1,2 1,6   2,0 2,4 2,8 3,2 3,6   4,0 4,4 4,8 5,2 5,6   6,0 6,4 6,8 7,2 7,6   8,0 8,4 8,8 9,2 9,6	1,000 0,949 0,756 0,547 0,390   0,285 0,214 0,165 0,130 0,106   0,087 0,073 0,062 0,053 0,046   0,040 0,036 0,032 0,028 0,024   0,022 0,021 0,019 0,018 0,016   0,015 0,011 0,009	1,000 0,960 0,800 0,606 0,449   0,336 0,257 0,201 0,160 0,130   0,108 0,091 0,077 0,066 0,058   0,051 0,045 0,040 0,036 0,032   0,029 0,026 0,024 0,022 0,20   0,019 0,017 0,015	1,000 0,968 0,830 0,652 0,496   0,379 0,294 0,232 0,187 0,153   0,127 0,107 0,092 0,079 0,069   0,060 0,053 0,048 0,042 0,038   0,035 0,032 0,029 0,026 0,024   0,022 0,020 0,018	1,000 0,972 0,848 0,682 0,532   0,414 0,325 0,260 0,210 0,173   0,145 0,122 0,105 0,091 0,079   0,070 0,062 0,055 0,049 0,044   0,040 0,037 0,034 0,031 0,028   0,026 0,023 0,020	1,000 0,974 0,859 0,703 0,558   0,441 0,352 0,284 0,232 0,192   0,161 0,137 0,118 0,102 0,089   0,078 0,070 0,062 0,056 0,050   0,046 0,042 0,038 0,035 0,032   0,030 0,027 0,024	1,000 0,975 0,866 0,717 0,578   0,463 0,374 0,304 0,251 0,209   0,176 0,150 0,130 0,112 0,099   0,087 0,077 0,069 0,062 0,056   0,051 0,046 0,042 0,039 0,036   0,033 0,029 0,026	1,000 0,976 0,870 0,727 0,593   0,481 0,392 0,321 0,267 0,224   0,190 0,163 0,141 0,123 0,108   0,095 0,085 0,076 0,068 0,062   0,056 0,051 0,047 0,043 0,040   0,037 0,033 0,028	1,000 0,976 0,875 0,740 0,612   0,505 0,419 0,350 0,294 0,250   0,214 0,185 0,161 0,141 0,124   0,110 0,098 0,088 0,080 0,072   0,066 0,060 0,055 0,051 0,047   0,044 0,040 0,034	1,000 0,977 0,878 0,746 0,623   0,520 0,437 0,369 0,314 0,270   0,233 0,203 0,178 0,157 0,139   0,124 0,111 0,100 0,090 0,082   0,075 0,069 0,063 0,058 0,054   0,050 0,044 0,038	1,000 0,977 0,879 0,749 0,630   0,529 0,449 0,383 0,329 0,285   0,248 0,218 0,192 0,170 0,152   0,136 0,122 0,110 0,100 0,091   0,084 0,077 0,070 0,065 0,060   0,056 0,050 0,044	1,000 0,977 0,880 0,753 0,636   0,540 0,462 0,400 0,348 0,305   0,270 0,239 0,213 0,191 0,172   0,155 0,141 0,128 0,117 0,107   0,098 0,091 0,084 0,078 0,072   0,067 0,060 0,051	1,000 0,977 0,881 0,754 0,639   0,545 0,470 0,410 0,360 0,320   0,285 0,256 0,230 0,208 0,189   0,172 0,158 0,144 0,133 0,123   0,113 0,105 0,098 0,091 0,085   0,079 0,071 0,060	1,000 0,977 0,881 0,755 0,642   0,550 0,477 0,420 0,374 0,337   0,306 0,280 0,258 0,239 0,223   0,208 0,196 0,184 0,175 0,166   0,158 0,150 0,144 0,137 0,132   0,126 0,114 0,104
П р и м е ч а н и е. Для промежуточных значений n и m величина коэффициента определяется интерполяцией.

При нагрузке, распределенной по прямоугольной площадке по закону треугольника, вертикальные нормальные напряжения по вертикали, проходящей через угловую точку с координатами

x = - l₁ и у = - b₁ ,

σ		=	p		π	+	4l1b1 z(4l12+4b12+2z2)	+
z	2π		(4b12+z2) (4l12+z2)√4l12+4b12+z2

+	b1 z3
l1(4l12+z2) √4l12+4b12+z2

-	b1 z
l1√4b12+z2

-

-arctg	z√4l12+4b12+z2
4l1 b1

определяются суммированием напряжений (рис. 1).

Наиболее распространенный случай в практике проектирования – учет взаимного влияния нескольких прямоугольных фундаментов. При этом широко используется метод угловых точек. Метод заключается в том, что

вертикальные нормальные напряжения σ_z,А на глубине z по вертикали,

проходящей через произвольную точку А (в пределах или за пределами рассматриваемого фундамента с давлением по подошве, равным р), определяются алгебраическим суммированием напряжений σ^с_z,i в угловых точках четырех фиктивных фундаментов (рис. 2)

σz,А	=	Σ	σ	c		(6)
z,J
		J=1

где σ^с_z,J вертикальное нормальное напряжение, определяемое по формуле (2).

Вертикальные нормальные напряжения σ_z по вертикали, проходящей через центр рассчитываемого фундамента, с учетом влияния соседних фундаментов или нагрузок на прилегающие площади определяются по формуле:

				к
σz	=	σ'z	+	Σ	σ	c		(7)
z,А,i
				i=1

где σ'_z - напряжение от нагрузок на рассматриваемый фундамент,

k - число влияющих фундаментов;

σ_z,А,i - дополнительное вертикальное нормальное напряжение на глубине z от i-го влияющего фундамента.

Задача

Требуется построить эпюры вертикальных нормальных напряжений σ_z по вертикалям, проходящим через центры двух смежных фундаментов Ф-1 и Ф-2 с учетом их взаимного влияния (рис. 1).

Задание по последней цифре учебного шифра (208914):

№
R0 (кПа)
l (м)
b (м)
С(м)	0,5

Здесь С – расстояние между осью Х₁ для Ф₁ и осью Х₂ для Ф₂ (рис. 1).

Расчет

Значение σ_z по оси фундамента Ф-1 получаем суммированием напряжений σ_z1 от давления р₀ под самим фундаментом и дополнительного напряжения σ_z2 от влияния фундамента Ф-2. Последнее определяем методом угловых точек как сумму напряжений на рассматриваемой глубине в угловой точке М четырех загруженных площадей (фиктивных фундаментов): MLAI и MNDL с положительным давлением р₀ и MKBI и MNCK – с отрицательным.

Соотношение сторон указанных прямоугольников равны: для EFGH (Ф-1) η =4/3=1,3; для MLAI и MNDL η =6,5/2=3,25; для MKBI и MNCK η =3,5/2=1,75.

Разбиваем основание на слои толщиной ∆h=0,8 м. При этом

∆ζ =2∆h/b=2*0.8/3=0.53;

∆ζ ₁ = ∆h/b=0.8/3=0.27 (см. формулы (1-5)).

Вычисления сводим в таблицу (2), в которой коэффициенты затухания напряжений по вертикали, проходящей через точку М относятся к прямоугольникам: α₁- EFGH (Ф-1); α₂ - MLAI и MNDL; α₃ - MKBI и MNCK; α₄ - ABCD (Ф-2),определен с учетом формул (5) и (6):

α₄=2 ^1/₄ (α₂ - α₃); α = α₁ + α₄ учитывает влияние нагрузок на фундаменты

Ф-1 и Ф-2 (значения коэффициентов а приняты по табл.1).

Таблица 2

Z,м	ζ	α1	α2	α3	α4	α	Напряжения, кПа
σz1=р0α1	σz2=р0α4	σ z=р0α
		1,000	1,000	1,000		1,000
0,8	0,53	0,927	0,945	0,931	0,007	0,934	264,2	1,99	266,2
1,6	1,06	0,727	0,794	0,769	0,013	0,740	207,2	3,70	210,9
2,4	1,6	0,514	0,630	0,578	0,013	0,540	146,5	7,41	153,9
3,2	2,13	0,367	0,503	0,434	0,034	0,436	104,6	9,69	124,3
4,0	2,66	0,268	0,406	0,328	0,039	0,307	76,4	11,11	87,5
4,8	3,2	0,198	0,333	0,251	0,041	0,239	56,4	11,68	68,1
5,6	3,73	0,154	0,273	0,198	0,037	0,196	43,9	10,54	54,4
6,4	4,26	0,122	0,228	0,159	0,034	0,156	34,8	9,69	44,5
7,2	4,8	0,098	0,192	0,130	0,031	0,129	27,9	8,83	36,8
8,0	5,33	0,081	0,164	0,108	0,028	0,109	23,1	7,98	31,1
8,8	5,86	0,068	0,142	0,091	0,025	0,093	19,4	7,12	26,6

Определение вертикальных нормальных напряжений от собственного веса грунта

Теория

Вертикальное нормальное напряжение σ_z от собственного веса грунта определяется по формуле

		n
σz	=	Σ	γihi,		(8)
,
		i=1

где n – число слоев грунта, расположенных выше рассматриваемой глубины;

γ_i - удельный вес грунта i-го слоя; h_i - толщина i-го слоя грунта.

Удельный вес грунтов, залегающих ниже уровня подземных вод, но выше водоупора, определяется с учетом взвешивающего действия воды по формуле

γsb	=	(γs	-	γω)	/ (1+e),		(9)

где γ_s - удельный вес частиц грунта; γ_ω - удельный вес воды, принимаемый равным 10кН/м3; е – коэффициент пористости грунта.

Если удельный вес грунта определен при его полном водонасыщении (степень влажности Sr =1, γ = γ_sat ), то

γsb	=	(γsat	-	γω)	(10)

При определении σ_z от собственного веса грунта в водоупорном слое необходимо учитывать давление столба воды, расположенного выше водоупора.

Горизонтальные нормальные напряжения от собственного веса грунта

σx

=

σy

=

ξ

σz,

(11)

где ξ= μ(1- μ) - коэффициент бокового давления грунта (здесь –коэффициент поперечной деформации, принимается по табл. )

таблица μ

грунты	μ
Пески Супеси Суглинки Глины	0,28 0,31 0,37 0,41

Задача

Определить вертикальное нормальное напряжение σ_z от собственного веса грунта на глубине z = 9м при грунтовых напластованиях, показанных на рисунке 2:

Верх 4-ого слоя-водоупор

N, кН/м3
γ1	15,35
γ2	17,6
γ3	20,3
γ4	20,5
h1 (м)
h2 (м)
h3 (м)
h4 (м)
УГВ(м)	1,5
е	0,58

Расчет

Слой 1 – суглинок

толщина слоя h₁= 1,5м. выше уровня гровня грунтовых вод, h₁= 0,5м. ниже уровня грунтовых вод;

удельный вес γ₁ = 15,35 кН/м3;

удельный вес воды γ_ω =10 кН/м3;

е = 0,58 – коэфициент пористости.

γsb1	=	(15,35	-	10)	/ (1+0,58) = 3,38 кН/м3.

Слой 2 – песок средней крупности h₂ = 1 м.

удельный вес частиц γ₂ =17,6 кН/м3;

удельный вес воды γ_ω =10 кН/м3;

γ_sb2 = 17,6 - 10=7,6 кН/м3.

Слой 3 – песок средней крупности h₃ = 4 м.

удельный вес частиц γ₃ = 20,3 кН/м3;

удельный вес воды γ_ω =10 кН/м3;

γ_sb3 = 20,3 - 10=10,3 кН/м3.

Слой 4 – глина, служащая водоупором h₄ = 1 м.

удельный вес частиц γ₄ =20,5 кН/м3;

По формуле (8) на глубине z = 9 м получаем:

σ_z = 1,5*15,35 +0,5*3,38 +1*7,6 +4*10,3+20,5*1+5,5*10 = 149,02кПа

Значения ординат эпюры σ_z приведены на рисунке 2.

Определение расчетного сопротивления грунта основания для песков

Теория

Для вычисления расчетного сопротивления грунта основания используется формула

R= γ_c1-γ_c2/ K ^. (М_γК_z x bγ₁₁+М_q x d₁γ´₁₁+(М_q-1) x d_в γ´₁₁+М_c x C₁₁) (12)

d₁=h_s+h_cf ^. γ _cf / γ₁₁

_{где Kz = 1; K= 1,1}

Таблица 2. Значения коэффициентов γ_с1 и γ_с2

Грунты	γс1	γс2 для сооружений с жесткой конструктивной схемой при отношении длины сооружения или его отсека к его высоте L/H
>4	< 1.5
Крупнообломочные с песчаным заполнителем и песчаные кроме мелких и пылеватых   Пески мелкие   Пески пылеватые: · маловлажные и влажные · насыщенные водой · Крупнообломочные с пылевато-глинистым заполнителем и пылевато-глинистые с показателем текучести грунта или заполнителя: · I L ≤ 0.25 · 0.25< I ≤0.5 · I L > 0.5	1,4   1,3     1,25 1,1     1.25 1.2 1.1	1,2   1,1     1,0 1,0     1.0 1.0 1.0	1,4   1,3     1,2 1,2     1.1 1.1 1.0

Примечания:

1. Жесткую конструктивную схему имеют сооружения, конструкции которых приспособлены к восприятию усилий от деформаций оснований путем применения специальных мероприятий

2. Для сооружений с гибкой конструктивной схемой значение коэффициента γ_с2 принимается равным единице

3. При промежуточных значениях L/H коэффициент γ_с1 определяется интерполяцией

Таблица 3. Значения коэффициентов М_γ, М_q, М_c

Φ11˚	М γ	Мq	Мc	φ 11˚	М γ	Мq	Мc
			3,14		0,69	3,65	6,24
	0,01	0,06	3,23		0,72	3,87	6,45
	0,03	1,12	3,32		0,78	4,11	6,67
	0,04	1,18	3,41		0,84	4,37	6,90
	0,06	1,25	3,51		0,91	4,64	7,14
	0,08	1,32	3,61		0,98	4,93	7,40
	0,10	1,39	3,71		1,06	5,25	7,67
	0,12	1,47	3,82		1,15	5,59	7,95
	0,14	1,55	3,93		1,24	5,95	8,24
	0,16	1,64	4,05		1,34	6,34	8,55
	0,18	1,73	4,17		1,44	6,76	8,88
	0,21	1,83	4,29		1,55	7,22	9,22
	0,23	1,94	4,42		1,68	7,71	9,58
	0,26	2,06	4,55		1,81	8,24	9,97
	0,29	2,17	4,69		1,95	8,81	10,37
	0,32	2,30	4,84		2,11	9,44	10,80
	0,36	2,43	4,99		2,28	10,11	11,25
	0,39	2,57	5,15		2,46	10,85	11,73
	0,43	2,73	5,31		2,66	11,64	12,24
	0,47	2,89	5,48		2,88	12,51	12,79
	0,51	3,06	5,66		3,12	13,46	13,37
	0,56	3,24	5,84		3,38	14,50	13,98
	0,61	3,44	6,04		3,66	15,64	14,64

Коэффициенты М _γ, М _q и М_c, получены исходя из условия, что зоны пластических деформаций под краями равномерно загруженной полосы (рис.5) равны четверти ее ширины и вычисляются по следующим соотношениям:

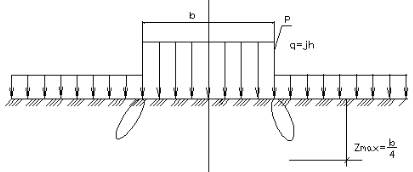
Рис. 5. Зоны пластических деформаций в основании под краями равномерно загруженной полосы.

М _γ= ψ /4; М _q= 1+ ψ; М_c= ψctg φ₁₁ ; (13)

где ψ=π/(ctg φ₁₁₊ φ₁₁- π/2); φ₁₁ - расчетное значение угла внутреннего трения, рад.

При вычислении R значения характеристик φ_11, с_11, и γ₁₁ принимаются для слоя грунта, находящегося под подошвой фундамента до глубины z_R = 0,5 b при b<10 м и z_R = t +0.1 b при b≥ 10 м (здесь t = 4 м). При наличии нескольких слоев грунта от подошвы фундамента до глубины z_R принимаются средневзвешенные значения указанных характеристик.

Аналогичным образом поступают и с коэффициентами γ_{с1 и} γ_с2.

Значение R зависит не только от физико-механических характеристик грунтов основания, но и от искомых геометрических размеров фундамента – ширины и глубины его заложения. Поэтому определение размеров фундаментов приходится вести итерационным способом, задавшись предварительно какими-то начальными размерами.

Задача

Определить расчетное сопротивление грунта основания для ленточного фундамента шириной b = 1,4 м. при следующих исходных данных. Проектируемое здание – 9 - этажное крупнопанельное с жесткой конструктивной схемой. Отношение длины его к высоте L/H =1,5 м. Глубина заложения фундаментов от уровня планировки по конструктивным соображениям принята d =1,7 м. Здание имеет подвал шириной B = 12 м и глубиной d_b =1,10 м. Толщина слоя грунта от подошвы фундамента до пола подвала h_s = 0,3 м, толщина бетонного пола подвала h_cf = 0,3 м, удельный вес бетона γ_cf = 23 кН/м3. Площадка сложена песками мелкими средней плотности маловлажными. Коэффициент швы γ´₁₁ = 17 кН/м3. Нормативные значения прочностных и деформацпористости е = 0,74, удельный вес грунта ниже подошвы γ₁₁= 18 кН/м3, выше подоионных характеристик приняты по справочным таблицам:

φ_n= φ₁₁= 23˚, с_n = с₁₁ = 2 кПа, Е = 28 MПа

Задание по последней цифре учебного шифра

№
h cf (м)	0,30
d b (м)	1,10
φ11˚(град)
С11 (кПа)	1,9

Задача

Для вычисления расчетного сопротивления грунта основания используется формула

R= γ_c1-γ_c2/ K ^. (М_γК_z x bγ₁₁+М_q x d₁γ´₁₁+(М_q-1) x d_в γ´₁₁+М_c x C₁₁) (12)

d₁=h_s+h_cf ^. γ _cf / γ₁₁

_{где Kz = 1; K= 1,1}

для песка мелкого маловлажного и здания жесткой конструктивной схемы при L/H=1.5, γ_c1=1,3 и γ_c2 =1,3; по табличным данным при φ₁₁ =23,

М_γ = 0,69; М_q = 3,65; и М_c = 6,24. Поскольку значения прочностных характеристик грунта приняты по справочным таблицам, k=1,1

При b = 1,4 м < 10 м. k_z =1.

Приведенная глубина заложения фундаментов от пола подвала по формуле

d₁ = 0.3+0.3 * 23/17 = 0,7 м.

Определяем расчетное сопротивления грунта основания:

R=1.3x1.3/1.1[0,69*1*1.4*18+3,65*0,7*17+(3,65-1)*1,1*17+6,24*1,9] =

=1,54*122,234=188,24 кПа.

Предварительные размеры фундаментов назначаются по конструктивным соображениям или, исходя из значений расчетного сопротивления грунтов основания, приведенных в табл. 4.

Таблица 4. РАСЧЕТНЫЕ СОПРОТИВЛЕНИЯ R₀ КРУПНООБЛОМОЧНЫХ

ПЕСЧАННЫХ И ПЫЛЕВАТОГЛИН ИСТЫХ (НЕПРОСАДОЧНЫХ) ГРУНТОВ

Грунты	R0, КПа
Крупнообломочные   Галечниковый (щебенистый) с заполнителем: Песчаным Пылевато- глинистым Гравий (дресвяный): с заполнителем: Песчаным Пылевато глинистым	450/400   400/350

Значения R₀ при показателе текучести I_L ≤0.5 даны перед чертой,

при 0.5< I_L ≤0.75 - за чертой.

Пески
Крупные Средней крупности Мелкие: маловлажные влажные и насыщенные водой   Пылеватые: маловлажные влажные насыщенные водой	600/500 500/400   400/300 300/200     300/250 200/150 150/100

Значения R₀ для плотных песков даны перед чертой,

для песков средней плотности - за чертой.

Пылевато- глинистые
Супеси с коэффициентом пористости е: 0,5 0,7 Суглинки с коэффициентом пористости е: 0,5 0,7 1,0 Глины с коэффициентом пористости е: 0,5 0,6 0,8 1,0	300/300 250/200   300/250 250/180 200/100     600/400 500/300 300/200 250/100

Значения R₀ при I_L=0 даны перед чертой, при I_L=1 - за чертой. При промежуточных значениях е и I_L значения R₀ определяются интерполяцией.

Значениями R₀ допускается также пользоваться для окончательного назначения размеров фундаментов сооружений III класса, если основания сложено горизонтальными (уклон не более 0,1) выдержанными по толщине слоями, грунта, сжимаемость которых не увеличивается с глубиной в пределах двойной ширины наибольшего фундамента ниже глубины его заложения.

Двойную интерполяцию при определении Р₀ по табл. 4. Для пылевато-глинистых грунтов с промежуточными значениями I_L и е рекомендуется выполнять по формуле (15)

R₀ (e, I_L) = (e₂ – e)/(e₂ - e₁ )[ (1 - I_L) R₀ (1, 0) + I_L R₀ (1, 1)] +

(e - e₁)/(e₂ - e₁₎[(1- I_L) x R₀ (0, 0) + I_L R₀ (2, 1)] (15)

где e₁ и e₂ - соседние значения коэффициента пористости в табл. 3 между которыми находится значение е для рассматриваемого грунта;

R₀ (1, 0) и R₀ (1, 1) – значения R₀ в табл. 4 при коэффициенте пористости е₁, соответствующие значениям I_L=0 и I_L=1;

R₀ (2, 0) и R₀ (2, 1) - то же, при е₂.

Значения R₀ в табл. 4 относятся к фундаментам, имеющим ширину b₁ и глубину заложения d₁ м. При использовании значений R₀ по табл.4 для окончательного назначения размеров фундаментов расчетное сопротивление грунта основания R определяется по формулам:

при d₁ ≤ 2м

R = R₀ [1 + k₁ (b - b₁ / b₁ ) ] (d + d₁ / 2d₁); (16)

при d₁ > 2м

R = R₀ [1 + k₁ (b - b₁ / b₁ ) ] + k₂ γ´(d - d₁) (17)

где b и d - соответственно ширина и глубина заложения проектируемого фундамента, м;

γ´-удельный вес грунта расположенного выше подошвы фундамента, кН/м3;

k₁ - коэффициент принимаемый для крупнообломочных и песчаных грунтов (кроме пылеватых песков) k₁=0,125 а для пылеватых песков, супесей, суглинков и глин k₁=0,05;

k₂ - коэффициент принимаемый для крупнообломочных и песчаных грунтов k₂ = 2,5 а для супесей, суглинков k₂ = 2, а для глин k₂ =1,5.