Определение объёмного расхода
| pат |

| Вода |
| Ртуть |
| ζп |
| Ф |
| p0 |
| lвс, dвс, ΔЭ1 |
| M1 |
| A |
| II |
| II |
 Для определения расхода следует проанализировать первую часть схемы
Для определения расхода следует проанализировать первую часть схемы (рис. 24). Последовательность действий реализуем в соответствии с рекомендациями.
а) Плоскость сравнения 0-0 наиболее удобно провести по уровню воды в баке. В этом случае все геометрические высоты будут положительными.
б) Живое сечение потока I-I удобно расположить по поверхности воды, сечение II-II – в точке А. Выбор сечений обусловлен тем, что практически все параметры этой части схемы сосредоточены именно в этих сечениях.
в)
| Рис. 24. Первая часть схемы |
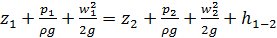 .
.
г) Проведём идентификацию параметров уравнения Бернулли: z1=0, p1=p0, w1≈0; z2=hвс, p2=pA, w2=?, h1-2 – потери напора между резервуаром и насосом. Потери напора необходимо расписать подробнее. На этом участке схемы два местных сопротивления – фильтр и поворот со своими коэффициентами сопротивления. Кроме того необходимо учесть потери на трение по формуле Д’Арси. В итоге получаем
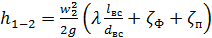 .
.
Давление p0 неизвестно, но есть показание манометра М1, отсюда следует, что
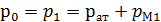 .
.
В точке А расположен жидкостный U-образный манометр с известными высотами столбов жидкостей, что позволяет определить абсолютное давление в сечении II-II
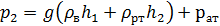 .
.
д) Выписываем уравнение Бернулли с применением исходных данных
 .
.
После приведения подобных и группировки слагаемых получается следующее выражение
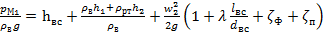 .
.
е) Полученное уравнение легко разрешается относительно неизвестной скорости w2
 .
.
В этом соотношении необходимо определить коэффициент трения, который в общем случае сам зависит от скорости. Полученное уравнение по отношению к скорости с учётом коэффициента трения является трансцентдентым и решается методом последовательного приближения. В первом приближении пренебрегаем потерями на трение:

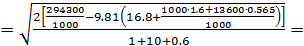 1,8198 м/с.
1,8198 м/с.
Необходимо помнить, что 1 кГ (килограмм силы) равен 9,81 Н.
Для уточнения скорости оценим величину коэффициента трения. Определим значение критерия Рейнольдса
 .
.
Значение критерия Рейнольдса указывает на турбулентное течение и на необходимость использования логарифмических формул для коэффициента трения. Определим область сопротивления:
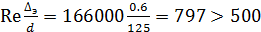 .
.
Это означает, что труба гидравлически шероховатая и коэффициент трения следует определять по формуле Никурадзе
 .
.
Уточняем значение скорости
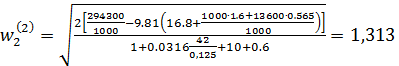 м/с.
м/с.
Проверим область сопротивления.
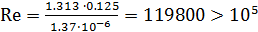 ;
;
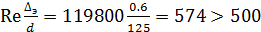 .
.
Труба осталась в области квадратичного сопротивления, откуда следует, что коэффициент трения не зависит от скорости и второе приближении скорости можно считать окончательным значением.
Определяем расход воды
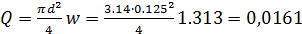 м3/с=16,1 л.
м3/с=16,1 л.
Основная цель анализа первой части схемы выполнена.
6.3. Определение показания манометра М2
Для определения показания следует проанализировать вторую часть схемы (рис. 25). Последовательность действий реализуем в соответствии с рекомендациями по аналогии с первой частью схемы.
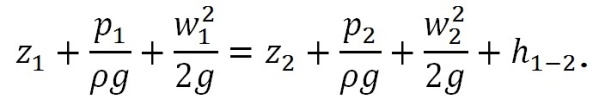
| M3 |
| ζ1 |
| ζ2 |
| M2 |
| H |
| Др |
| l, d, ΔЭ2 |
| p0 |
| В |
| II |
| II |

 Плоскость сравнения 0-0 проведём на уровне точки B. Живое сечение I-I проведём через точку В, второе II-II – по поверхности воды в резервуаре. Выписываем уравнение Бернулли в напорах
Плоскость сравнения 0-0 проведём на уровне точки B. Живое сечение I-I проведём через точку В, второе II-II – по поверхности воды в резервуаре. Выписываем уравнение Бернулли в напорах Рис. 25. Вторая часть схемы
Идентифицируем параметры уравнения: z1=0, p1=pВ, w1=?; z2=Н, p2=p0, w2≈0, h1-2 - потери напора между насосом и резервуаром. Потери напора необходимо расписать подробнее. На этом участке схемы три местных сопротивления – дроссель и два поворота. Кроме того необходимо учесть потери на трение по формуле Д’Арси. В итоге получаем
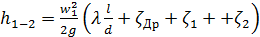 .
.
Так как излив в резервуар происходит на поверхность жидкости в баке, сопротивление входа в резервуар можно не учитывать.
Давление p0 неизвестно, но есть показание манометра М3:
 .
.
Давление pB неизвестно, так как неизвестно показание манометра М2. Тем не менее, расписываем это давление
 .
.
Выписываем уравнение Бернулли с применением исходных данных
 .
.
После приведения подобных разрешаем это уравнение относительно показания манометра М2
 .
.
Это уравнение с двумя неизвестными: pM2 и w1. Так как расход в системе уже определён, то можно воспользоваться уравнением баланса расходов, откуда
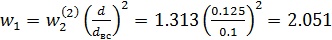 м/с.
м/с.
Определим коэффициент трения.
 .
.
 .
.
Труба гидравлически шероховатая и коэффициент трения следует определять по формуле Никурадзе
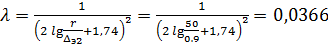 .
.
Теперь уравнение даёт возможность определить давление pM2
 ,
,
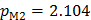 МПа.
МПа.
Основная цель анализа второй части схемы выполнена.
