Ошибки нанесения делений на лимб. Способы ослабления их влияния
Деления на лимбе наносят с помощью автоматической делительной машины. Вследствие действия ряда причин (например, погрешности установки лимба на ось вращения машины, вибрации машины во время ее работы, изменения температуры и т.д.) эти деления наносятся с некоторыми ошибками.
Обозначим через φ и (φ+180°) фактические положения двух любых диаметрально противоположных штрихов лимба, а через  и
и  - ошибки нанесения этих штрихов. При угловых измерениях отсчеты берутся по диаметрально противоположным штрихам лимба, т.е. всегда используются диаметры лимба, которые характеризуются ошибкой
- ошибки нанесения этих штрихов. При угловых измерениях отсчеты берутся по диаметрально противоположным штрихам лимба, т.е. всегда используются диаметры лимба, которые характеризуются ошибкой  . Величину
. Величину  называют полной ошибкой диаметра φ.
называют полной ошибкой диаметра φ.
Полную ошибку 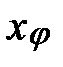 диаметра φ представляют в виде суммы систематической x
диаметра φ представляют в виде суммы систематической x  и случайной
и случайной 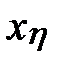 составляющих, т.е.
составляющих, т.е. 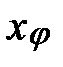 = x
= x  +
+ 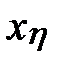 (6.10)
(6.10)
Полную 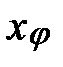 и систематическую x
и систематическую x  ошибки диаметровопределяют из исследований, а случайную - как разность
ошибки диаметровопределяют из исследований, а случайную - как разность 
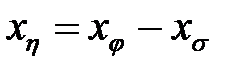 .
.
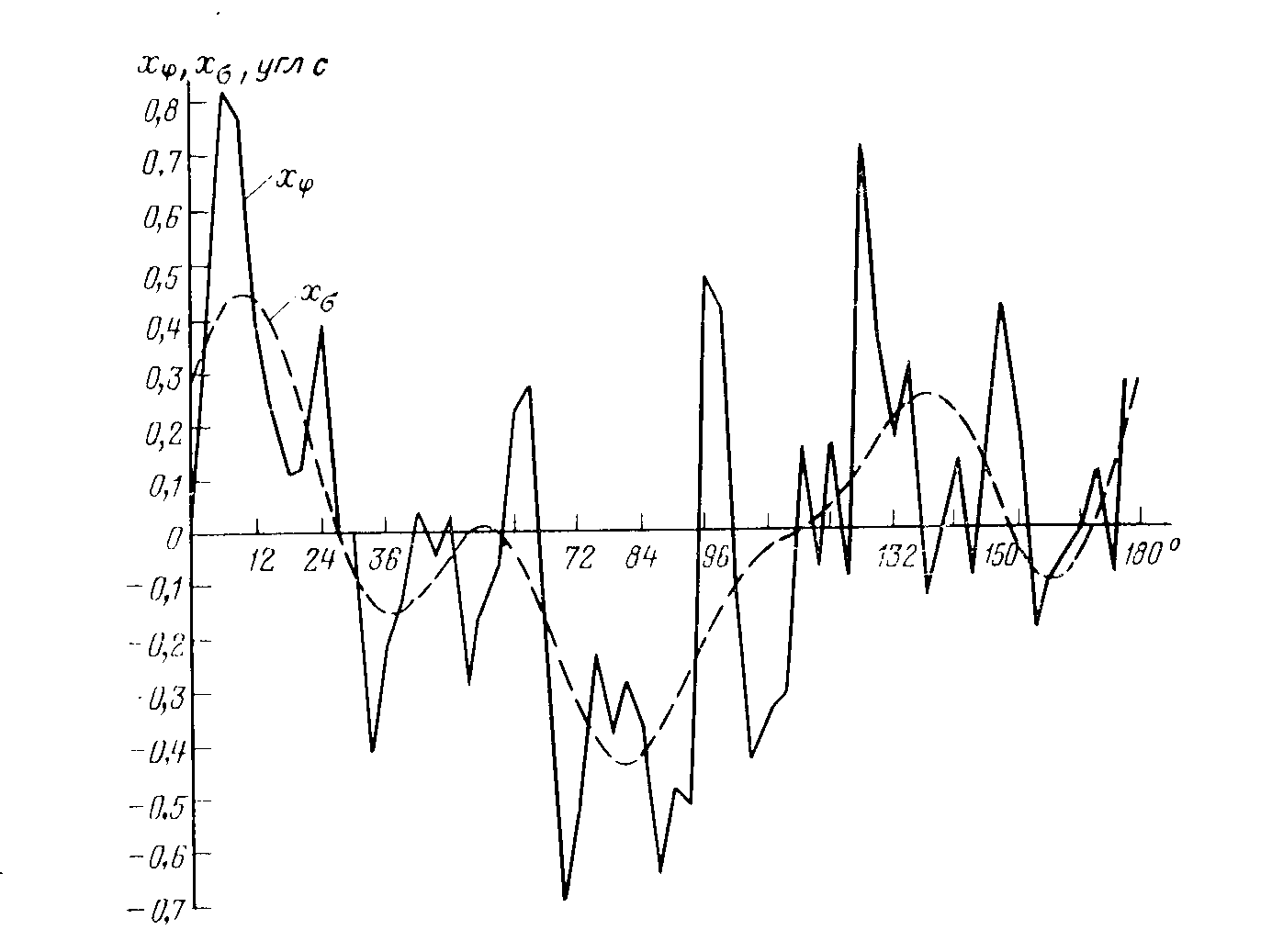
Полные  и систематические
и систематические 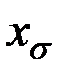 длиннопериодические ошибки диаметров лимба теодолита Т05
длиннопериодические ошибки диаметров лимба теодолита Т05
Ошибки диаметров подразделяются на длиннопериодические (рис. 6.3), т.е. изменяющиеся по всей окружности лимба, и короткопериодические (рис. 6.4),
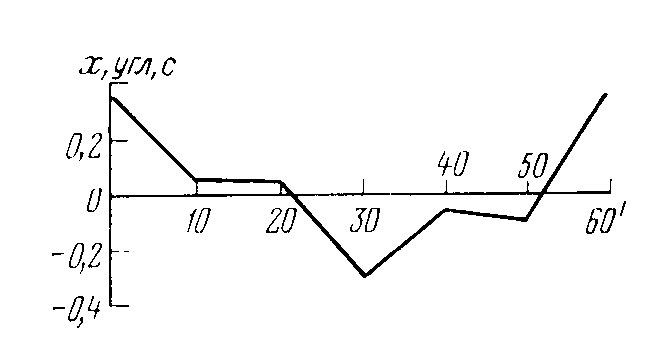 Рис. 6.4. Короткопериодические (внутриградусные) ошибки диаметров лимба теодолита Т05
Рис. 6.4. Короткопериодические (внутриградусные) ошибки диаметров лимба теодолита Т05
Допуск на 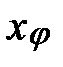 у современных теодолитов составляет ±(1¸1.2)".
у современных теодолитов составляет ±(1¸1.2)".
Ошибки диаметров круга непосредственно влияют на точность угловых измерений. Поэтому каждый лимб тщательно исследуют на его пригодность к высокоточным угловым измерениям.
Известны разные способы определения ошибок диаметра лимба: Пранис-Праневича, Елисеева, Литвинова, Шрейбера, Брунса и т.д. В основе всех способов определения ошибок диаметров лимба лежит последовательное измерение по определенной программе трех углов: b1 = 36°, b2 = 45°, b3 = 60° через интервал Dj = 3°.Обработку выполняют по СНК. Точность определения поправок диаметров характеризуется СКО ±0,1".
Способ ослабления влияния ошибок диаметров лимба на результаты угловых измерений основан на квазипериодическом характере их изменения как в пределах всей окружности (длиннопериодические рис. 6.3), так и внутри градуса (короткопериодические рис. 6.4). При выводе среднего арифметрического из ошибок диаметров, равномерно распределенных по всей окружности через одинаковые интервалы, происходит их значительная компенсация, причем, в тем большей мере, чем меньше эти интервалы.
Поэтому с целью максимальной компенсации ошибок диаметров круга (длинно и короткопериодических) в геодезии при измерении углов и направлений всегда переставляют горизонтальный круг теодолита между приемами на величину:
 или
или  (6.11)
(6.11)
