Где m – число приемов; i – цена наименьшего деления лимба

Компенсация будет тем полнее, чем больше приемов.

Данный способ перестановки горизонтального круга теодолита между приемами на угол d позволяет почти полностью скомпенсировать влияние на результаты угловых измерений систематических ошибок, а также существенно ослабить влияние случайных ошибок диаметров. У современных теодолитов ошибка диаметров лимба при 12 приемах измерений обычно не превышает 0,10" - 0,15".

14. Общие сведения о производстве высокоточных угловых измерений

На пунктах государственной треангуляции измеряют углы и горизонтальные направления. К методам измерения этих величин предъявляют следующие основные требования:

1. Программа наблюдений на пункте должна быть оптимальной, т.е. она должна обеспечивать:

а) равноточность результатов измерений на каждом отдельном пункте, а также на всех пунктах геодезической сети одного класса;

б) необходимую точность результатов при сравнительно небольших экономических затрат на производство работ;

в) строгость и простоту математической обработки результатов измерений на пункте.

2. Методика наблюдений на пункте должна гарантировать наиболее полное уменьшение влияния различного рода ошибок, т.е.:

а) максимально исключать влияние главных инструментальных ошибок (коллимационной ошибки, неравенство подставок, наклон вертикальной оси вращения теодолита). Для уменьшения двух первых влияний наблюдения в каждом приеме всегда выполняются при двух кругах: КЛ – 1-ый полуприем, КП – 2-ой полуприем; для уменьшения последнего влияния при углах наклона более двух градусов в методике необходимо предусмотреть возможность введения поправки за наклон вертикальной оси вращения теодолита (формула 6.9);

б) максимально исключать влияние ошибок диаметров лимба, для чего согласно формуле (6.11) между приемами следует делать перестановку лимба на величину (или + ) с целью равномерного использования всех участков лимба;

в) учитывать явление смещения лимба по азимуту в процессе наблюдения;

г) с целью максимального исключения неблагоприятного влияния внешних условий угловые измерения должны производиться при наилучших условиях видимости. Как правило, это период утренней видимости (начало, в среднем, спустя час после восхода солнца продолжительностью 1,5 -2 часа); период вечерней видимости (начинается примерно за 3 часа до захода солнца и заканчивается за 0,5 – 1 час до захода) и период ночных наблюдений (на светящиеся цели). Запрещается выполнять угловые измерения при наличии тумана, дымки, нечетких сильно колеблющихся изображениях, ветре. Практики - наблюдатели считают наилучшими слегка колеблющиеся изображения визирных целей.

3. Результаты измерений обязательно должны быть проконтролированы и оценены. Для этого на каждом пункте выполняются кроме необходимых еще и избыточные измерения.

Классическими способами измерения горизонтальных направлений и углов являются:

1. Способ круговых приемов (или способ Струве).

2. Способ всевозможных комбинаций (предложен Гауссом и усовершенствован Шрейбером).

Кроме того, известны еще некоторые видоизменения этих двух способов, которые в литературе тоже идут как самостоятельные, под именем авторов:

3. Способ Томилина или видоизмененный способ измерения углов всевозможных комбинаций.

4. Способ Аладжалова или способ неполных приемов.

19. Измерение горизонтальных направлений способом круговых приемов

Способ круговых приемов был предложен в 1816 году в России академиком Струве. Он получил широкое распространение во многих странах. В СССР способ круговых приемов применялся при построении триангуляционных сетей, начиная от 2 класса и ниже, в США – при построении триангуляции 1 класса и ниже.

Суть этого способа заключается в следующем.

Пусть мы имеем на пункте триангуляции n направлений (рис. 7.1).

aN

aС

aВ

aA

βC

βB

βA

βN

DI

Nn

С

В

А2

О (начальное)

Рис. 7.1. Иллюстрация к способу круговых приемов

DI — пункт наблюдения; O, A, B, C ...N - наблюдаемые пункты; 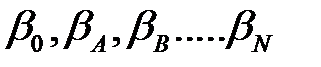- отсчеты по горизонтальному кругу на наблюдаемые направления, включая и начальное O.

— значения горизонтальных направлений относительно начального.

В способе круговых приемов при неподвижном лимбе вращением алидады по ходу часовой стрелки последовательно наводят зрительную трубу на направления O, A, B, C ...N и снова на начальное направление О (т. е. замыкают горизонт), отсчитывая каждый раз по горизонтальному кругу. Затем переводят трубу через зенит и наблюдают все направления уже в обратном порядке: О, N,…… C, B, A, O. Таким образом, каждый прием в данном способе состоит из двух полуприемов, порядок наблюдений в которых следующий:

1-ый полуприем КЛ: O, A, B, C ...N, О (вращение по ходу часовой стрелки) 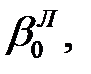….. (отсчеты при КЛ)

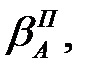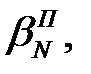
2-ой полуприем КП: О, N,… C, B, A, O (вращение против хода часовой стрелки) …… (отсчеты при КП)

За вес Р программы измерений в способе круговых приемов, как правило, принимается вес уравненного направления, устанавливаемого формулой

Р=2 m (7.1)

Вес уравненного угла в этом случае равен

Р_ур.у.=m, (7.2)

где m — число приемов.

Число приемов в зависимости от класса рассчитывается по формуле (7.1);

Р – устанавливается инструкцией.

Класс триангуляции
Р=2 m	24-30
Число приемов m	12-15

Между приемами всегда выполняется перестановка лимба на величину 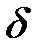, вычисляемую по формуле (6.11). Необходимая установка лимба в наблюдаемом приеме рассчитывается по формуле:

или (7.3)

где — установка лимба в приеме; m – число приемов; i – цена деления лимба; N – номер приема в программе наблюдений.

Контроли и допуски результатов угловых наблюдений на пункте рассматриваемым способом даны в таблице 7.1.

Таблица 7.1

Основные допуски в способе круговых приемов

Класс триангуляции
Внутри приема
Замыкание горизонта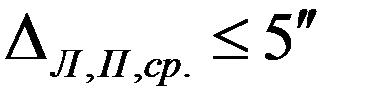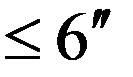
Коллимационная ошибка
Колебание коллимации в приеме
Между приемами
Расхождение значений направлений между приемами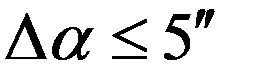
Число повторных приемов—направлений в программе	Не более 30%

7.3. Математическая обработка результатов угловых измерений на пункте в способе круговых приемов

Математическая обработка результатов угловых измерений в способе круговых приемов включает:

— обработку полевого журнала;

— составление сводной ведомости результатов угловых наблюдений на пункте с получением уравненных значений направлений и оценкой точности результатов измерений.

Обработка полевого журнала

Непосредственно в полевом журнале для каждого приема вычисляют:

а) коллимационную ошибку на каждое направление (рис.7.1) по формуле:

2 (7.4)

б) значение каждого направления относительно начального

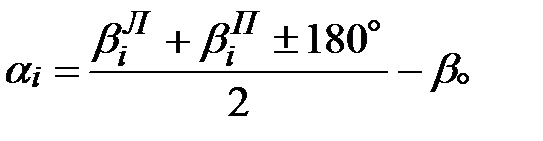, (7.5)

где , i — O, A,B,C……N (название наблюдаемого направления)

В значения направлений в каждом приеме вводят поправки:

1) За незамыкание горизонта

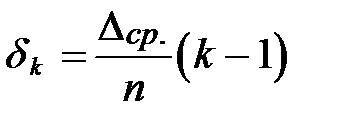, (7.6)

где D_ср. – незамыкание горизонта в приеме;

n - число наблюдаемых на пункте направлений;

k – порядковыйномер наблюдаемого направления в приеме.

2) За рен ( если r ³ 0^’’,5)

, (7.7)

где 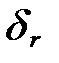- поправка за рен в наблюдаемое направление;

r –значение рена в секундах;

i' –цена деления лимба в минутах;

с' – отсчет по микрометру на наблюдаемое направление в минутах.

3) За наклон вертикальной оси инструмента (при углах наклона на направление ³2°):

(7.8)

В(7.8) b вычисляют по формуле (6.8).

Составление сводки результатов угловых наблюдений

Пример составления сводки приведен в инструкции и в соответствующей лабораторной работе настоящего УМК. Поэтому поясним только некоторые моменты процесса составления сводок.

Пусть на пункте I отнаблюдено n направлений m приемами по схеме, представленной на рис. 7.1. В результате обработки журнала мы имеем для каждого приема исправленные за все необходимые поправки значения горизонтальных направлений относительно начального направления О, где i - номер приема.

Вероятнейшие значения этих направлений на пункте выводятся из m приемов наблюдений из уравнивания по СНК. Так как согласно условию оптимальности программы наблюдений все измерения одного класса на пункте государственной триангуляции являются равноточными, то уравнивание по СНК в данном случае сводится к выводу средних значений направлений из m приемов (таблица 7.2).

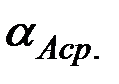
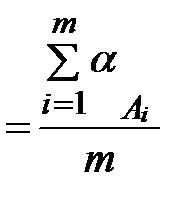; …………. (7.9)

Для каждого направления в приеме вычисляется отклонение v значения направления a_i от его среднего значения , выведенного из m приемов.

(7.10)

Правильность вывода среднего контролируется равенством (для каждого отдельного направления).

Оценка точности измеренных и уравненных величин на пункте в СКП

Для оценки точности результатов угловых измерений на пункте определяют СКО направления из одного приема и СКО уравненного угла М _.. и СКО уравненного направления М_н. из m приемов по формулам:

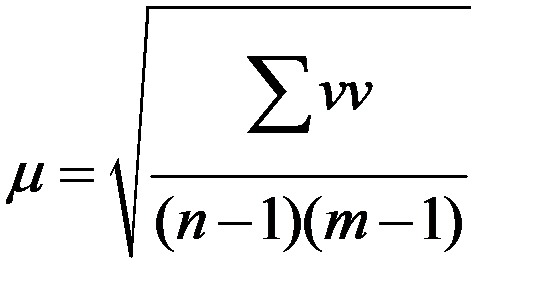(7.11)

На практике иногда вычисляют по упрощенной формуле Петерса:

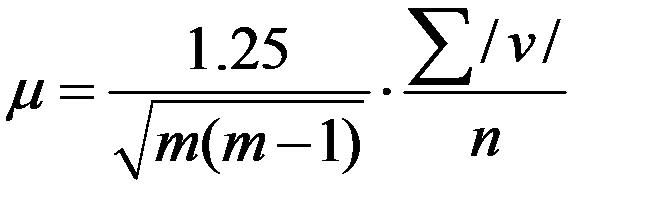= , (7.12)

где k в зависимости от числа приемов (6, 9, 12, 15) соответственно равно 0,23; 0,15; 0,11 и 0,08.

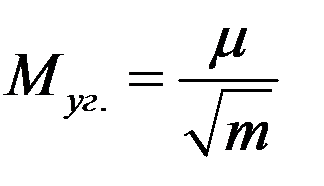; (7.13)

Достоинства и недостатки способа круговых приемов

Способ круговых приемов имеет следующие важные достоинства:

1. Простая программа наблюдений, позволяющая получить уравненные направления с одинаковыми весами.

2. Сравнительно большое число приемов непосредственных измерений каждого направления, что позволяет получить надежные результаты и ослабить влияние систематических ошибок лимба.

3. Простая математическая обработка.

4. Высокие технико - экономические показатели.

Недостатки:

1. Требует одновременной хорошей видимости на все направления. Поэтому его применение в горных районах довольно ограничено. В условиях Камчатского региона, например, способ круговых приемов почти не применяется.

2. Сравнительно большая продолжительность приема при числе направлений от 6 и более. (В среднем на наблюдение 1-ого направления тратится примерно 1 минута. Это приводит к заметному увеличению влияния погрешностей, возрастающих пропорционально времени (например, кручение сигнала).

Поэтому в способе круговых приемов в программу наблюдений разрешается включать не больше 7 направлений. При числе направлений на пункте больше 7 программу направлений разбивают на 2 и более группы с обязательным включением в каждую группу общего контрольного угла. Если, например, с пункта А необходимо отнаблюдать 9 направлений на пункты 1, 2, 3, 4, 5, 6, 7, 8, 9, то направления можно разбить на следующие 2 группы:

1-ая группа: с пункта A на направления 1, 2, 3, 4, 5

2-ая группа: с пункта А на направления 4, 5, 6, 7, 8, 9

Необходимость использования такого подхода приводит к увеличению объемов работ на пункте, а также к нарушению требования равноточности.

3. Повышенное требование к жесткости сигнала.