Построить логарифмическую амплитудно-частотную характеристику замкнутой системы, определить полосу пропускания системы, резонансную частоту, показатель колебательности
Им. Д.Ф. Устинова ВОЕНМЕХ
Кафедра мехатроники и робототехники
Курсовая работа по курсу Теория автоматического управления
Вариант 18
Студент: Шорохов А.С.
Группа: Н172.
Преподаватель: Коробова И.Л.
Санкт-Петербург
2009г.
Содержание
Определить передаточную функцию разомкнутой системы с коррекцией в цепи обратной связи и построить её логарифмические частотные характеристики.
Дать заключение об устойчивости замкнутой системы, определить запасы устойчивости.
Оценить показатели качества замкнутой системы, определив нули и полюса передаточной функции.
3. Построить графики переходной функции и импульсной переходной функции определить показатели качества переходного процесса (для оценки времени регулирования принять ∆=3%).
Найти аналитическое выражение импульсной переходной функции. Выделить составляющую найденной функции, соответствующую доминирующим полюсам, сравнить графики функции и указанной её составляющей.
Построить логарифмическую амплитудно-частотную характеристику замкнутой системы, определить полосу пропускания системы, резонансную частоту, показатель колебательности.
6. Найти уравнения состояния и выхода замкнутой системы. Проверить свойства управляемости и наблюдаемости этих вариантов.
- Определить передаточную функцию разомкнутой системы с коррекцией в цепи обратной связи и построить её логарифмические частотные характеристики:
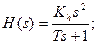
Передаточная функция разомкнутой системы:
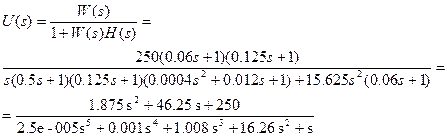
Приведем к каноническому виду, используя команду zpk в пакете Матлаб:
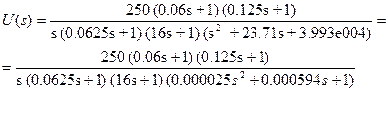
Находим ЛАЧХ и ФЧХ системы, используя пакет MATLAB:
>> num=[ 1.875,46.25,250];
>> den=[2.5e-005,0.001,1.008,16.26,1,0];
>> w=logspace(-3,3);
>> [gam,fi]=bode(num,den,w);
>> semilogx(w,20*log10(gam));
>> grid
>> title('L(w)')
>> semilogx(w,fi)
>> grid
>> title('fi')
>> title('fhase')
Рис.1
Рис.2
Дать заключение об устойчивости замкнутой системы, определить запасы устойчивости:
Разомкнутая система не имеет корней с положительной вещественной частью, поэтому
по критерию Найквиста, для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы ЛФЧХ разомкнутой системы в области частот, где ЛАЧХ положительна, принимала значение -180˚ четное число раз или не принимала этого значения, следовательно, данная система устойчива, т.к. ЛФЧХ не принимала значение 
ни разу в области частот, где ЛАЧХ положительна.
Используя функцию
>>u=w/(1+wh)
>>[g f wg wf]=margin(u)
в пакете Matlab определим:
-запас устойчивости по фазе f и соответствующая частота wf:
f= 37.6265, wf = 2.9608
-запас устойчивости по амплитуде g и соответствующая частота wg:
g = 10.8944
20*lg(g) =20*lg(10.8944)=20,7441,wg = 206.9531
Запас устойчивости по фазе определяется на частоте, при которой ЛАЧХ принимает значение 0.
Запас устойчивости по амплитуде определяется на частоте, при которой ФЧХ принимает значение -180˚.
Построим ЛАЧХ и ЛФЧХ разомкнутой системы, используя Матлаб(bode(u)):
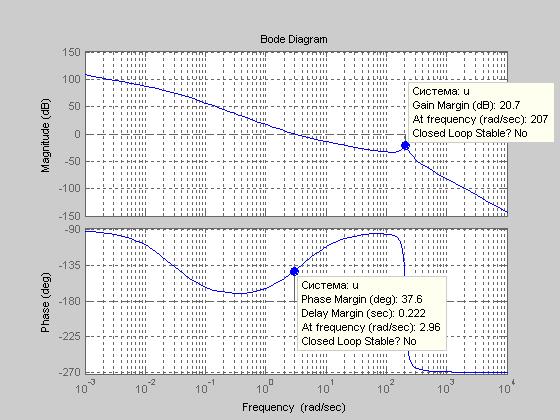
Рис.3
- Оценить показатели качества замкнутой системы, определив нули и полюса передаточной функции:
Определим передаточную функцию замкнутой системы:
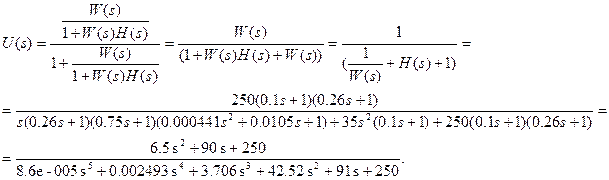
Найдем полюса и нули передаточной функции с использованием команд pole, zero:
>>s=tf('s');
>>w=(250*(0.1*s+1))/(s*(0.75*s+1)*(0.000441*s^2+0.0105*s+1))
>>h=(0.14*s^2)/(0.26*s+1)
>>u=w/(1+w*h)
>>ui=1/((1/w)+h+1)
>>pole(ui)
>>zero(ui)
Полюса(знаменатель)
ans =
1.0e+002 *
-0.0836 + 2.0690i
-0.0836 - 2.0690i
-0.0970
-0.0091 + 0.0248i
-0.0091 - 0.0248i
Нули (числитель)
ans =
-10.0000
-3.8462
Показатели качества:
Степень устойчивости:
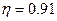
Время регулирования:
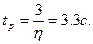
Степень колебательности:
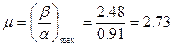
Колебательность связана с корневым показателем запаса устойчивости с так называемым затуханием. Комплексно сопряженные корни дают в выражении для переходного процесса вида
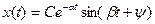
Найдем затухание амплитуды синусоидального колебания за один период. При некотором времени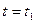 
эта амплитуда равна
Через один период 
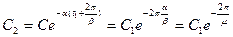
Затуханием за период называют величину
Подставляя значение амплитуды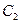 
, получаем
- Построить графики переходной функции и импульсной переходной функции определить показатели качества переходного процесса(для оценки времени регулирования принять ∆=3%):
Передаточная функция замкнутой системы:
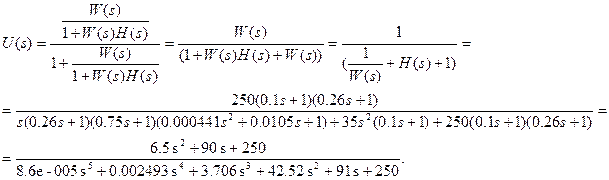
Построим графики переходных функций во временных осях, используя пакет Matlab и команды step(sys) и impulse(sys).
Код программы:
>>t=0:0.02:7
>>s=tf('s');
>>w=(250*(0.1*s+1))/(s*(0.75*s+1)*(0.000441*s^2+0.0105*s+1))
>>h=(0.14*s^2)/(0.26*s+1)
>>u=w/(1+w*h)
>>ui=1/((1/w)+h+1)
>>step(ui,t)
>>impulse(ui,t)
Показатели качества переходного процесса:
Апериодическая функция - т.к. 1 максимум.
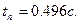- время, когда впервые достигается 
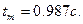-время достижения максимума.
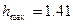
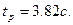-время регулирования.
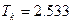
3%
Перерегулирование:
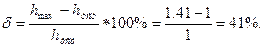
Частота колебаний:
n – число колебаний за время регулирования =2.