Простейшие расчеты притоков к скважинам
Движение воды к совершенной артезианской скважине (колодцу). Будем считать, что фильтрация имеет место в однородном (водопроводимость постоянная), горизонтально залегающем пласте, который подстилается водоупором. Тогда вода со всех сторон будет притекать к скважине равномерно через боковую поверхность цилиндра с радиусом r и высотой m (мощность пласта). На расстоянии rс от оси скважины существует напор Нс, а на расстоянии, равном радиусу влияния R обозначим через Не. = const. При этом величина понижения уровня Sr = R = 0. Напор на произвольном расстоянии от оси скважины r обозначим через Н. Напор будет изменяться от Нс, до Не при изменении радиуса от rс .до R. Расход потока определяется как
Q = kIF, где F – это боковая поверхность цилиндра с радиусом r. Тогда F = 2πrm, а напорный градиент I = dH/dr. Тогда расход запишется в виде:
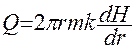 ( 39 )
( 39 )
Разделив переменные и подставив пределы интегрирования, имеем:
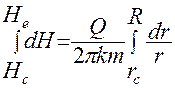 ( 40 )
( 40 )
Интегрирование этого уравнения дает:
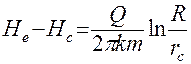 ( 41 )
( 41 )
Учитывая, что Не - Нс, = Sс то полученная формула пригодна для установившейся величины понижения (стационарный режим фильтрации) при производительности скважины Q.
Из ( 41 ) можно получить выражение для дебита совершенной скважины Q.
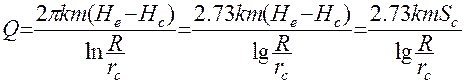 ( 42 )
( 42 )
Модификации формул ( 39) и ( 40 ) известны под названием формул Дюпюи.
Из ( 42 ) следует, что деьит напорной скважины связан с величиной понижения S линейной зависимостью, поскольку величина 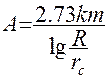 является для данной скважины постоянной. При этом Q = A·S. Коэффициент A представляет удельный дебит скважины q (приходящийся на 1 метр понижения уровня). Разделив обе части ( 42 ) на понижение Sс получим относительно А:
является для данной скважины постоянной. При этом Q = A·S. Коэффициент A представляет удельный дебит скважины q (приходящийся на 1 метр понижения уровня). Разделив обе части ( 42 ) на понижение Sс получим относительно А:
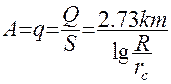 ( 43 )
( 43 )
При больших понижениях величина удельного дебита может не оставаться постоянной величиной.
Выражение ( 42 ) можно использовать также чтобы построить кривую депрессии. Можно определить понижение на S. любом расстоянии r от оси скважины. Для любого промежуточного сечения имеем:
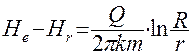 ( 44 )
( 44 )
Тогда напор на расстоянии r от оси скважины будет:
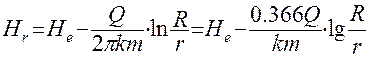 ( 45 )
( 45 )
Если ирасположить две наблюдательные скважины на расстояниях r1 и r2 и в них измерить положение уровня Н1 и Н2 то на любом другом расстоянии можно вычислить уровень Нr
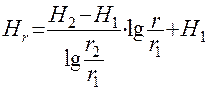 ( 46 )
( 46 )
и построить кривую депрессии. Если имеем только одну наблюдательную скважину, используют:
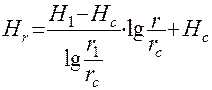 ( 47 ).
( 47 ).
Движение подземных вод к грунтовой совершенной скважине. Здесь мощность уже будет h и расход: 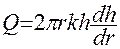 ( 48 )
( 48 )
После интегрирования в пределах r =rc, h =hc, r = R, h = He получим формулу для расхода
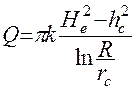 ( 49 )
( 49 )
Эту формулу можно получить исходя из решения для напорной скважины подставив 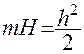 .
.
Действительно заменив в ( 42 ) m(He – Hc) на 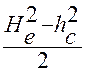 , получим формулу расхода:
, получим формулу расхода:
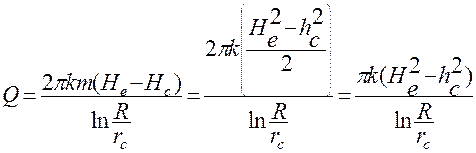 ( 50 )
( 50 )
Решая это уравнение относительно расхода Q получаем формулу производительности скважины, расположенной на расстоянии L от реки:
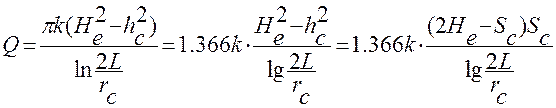 ( 51 )
( 51 )
Эта формула известна под названием формулы Ф. Форхгеймера.
Для совершенной артезианской скважины, расположенной у реки, с которым напорный поток имеет гидравлическую связь, расход выражается формулой:
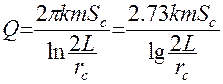 ( 52 )
( 52 )
Для определения величины понижения на стенке скважины из ( 52 ) можно получить выражение:
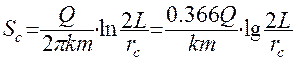 ( 53 )
( 53 )
 Лекция 5
Лекция 5
