Для расчета осадки воспользуемся методом послойного суммирования
Практика 2. Расчет оснований по деформациям (осадок фундаментов).
Содержание практического задания:
1. Теоретическая часть.
2. Пример практического задания.
3. Варианты заданий.
Теоретическая часть
Целью расчета оснований по деформациям является ограничение абсолютных или относительных перемещений фундаментов и надфундаментных конструкций такими пределами, при которых гарантируется нормальная эксплуатация сооружения и не снижается его долговечность (вследствие появления недопустимых осадок, подъемов, кренов, изменений проектных уровней и положений конструкций, расстройств их соединения и т.п.).
На практическом занятии будет рассмотрена осадка фундамента как пример расчета по деформациям оснований. Остальные случаи расчетов оснований по деформации: расчет просадок (на примере просадочных грунтов), подъемов (на примере набухающих грунтов) рассматриваются самостоятельно. Рекомендуемая литература СНиП 2.02.01-83 «Основания зданий и сооружений».
Осадка – деформации, происходящие в результате уплотнения грунта под действием внешних нагрузок и в отдельных случаях собственного веса грунта, не сопровождающегося коренными изменениями его структуры.
Прежде чем приступить к расчету осадок фундаментов необходимо иметь:
1. геологическое строение места строительства с указанием мощности отдельных слоев грунта, уровня грунтовых вод и, непременно, физико-механических свойств грунтов основания на всю активную зону сжатия (плотность, модуль деформации, коэффициенты пористости, сжимаемости, сопротивления сдвигу, а также для связных грунтов – коэффициенты фильтрации);
2. размеры и форму фундаментов (по предварительным расчетам) и чувствительность сооружений к неравномерным осадкам;
3. данные о глубине заложения фундаментов и нагрузке на грунт от надфундаментных конструкций.
Для расчета осадки воспользуемся методом послойного суммирования
Методы эквивалентного слоя (Н.А. Цытовича) и метод линейно деформируемого слоя конечной толщины (К.Е. Егорова) рассматриваются самостоятельно при использовании учебной литературы.
При использовании этого метода используются следующие теоритические предпосылки (см.рис.2.1).
 |
| Рис. 2.1. Теоретические предпосылки |
Слева вверху. Эпюры напряжения от собственного веса грунта представляют собой площадь фигуры в форме треугольника, ограниченного осями (ось напряжений и ось глубины) и линией, соединяющие значения эпюр напряжений. NL – отметка природного рельефа. FL – отметка подошвы фундамента.
Далее показано влияние сооружение котлована и удаление из него некоторого объема грунта на напряжения от собственного веса грунта и от нагрузки фундамента.
Справа вверху. Схема котлована под фундамент. Эпюры слева показывают напряжения от веса вынутого грунта. Представим, что вместо вынутого грунта снова приложена равная по характеристикам (давление, площадь) нагрузка. От нее возникнут напряжения. Эпюры от веса вынутого грунта будут иметь такой вид. Эпюры справа характеризуют напряжения от собственного веса грунта на дне котлована под фундамент при условии его обустройства. Эпюры напряжений после отрывки котлована вычисляются следующим образом: из напряжений от собственного веса грунта вычитают напряжения от собственного веса грунта, вынутого при отрывке котлована: 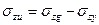 . Данная схема отражает это графически.
. Данная схема отражает это графически.
Внизу. На этой схеме показано влияние отрывки котлована под фундамент на напряжения от веса фундамента. Действие нагрузки от удаленного грунта аналогичное. Удаление грунта ведет к снятию какой-то степени нагрузки, в грунте наступает «релаксация» в результате, напряжения от нагрузки фундамента оказываются меньше на величину напряжений от собственного веса грунта, вынутого при отрывке котлована.
Для решения учебной задачи используются схема без заглубления фундамента, фундамент проектируется на земной поверхности, соответственно эпюры напряжений от собственного веса грунта имеют вид как на рис.2.1 слева вверху.
Общий вид формулы для послойного суммирования
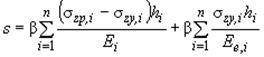 | где  - безразмерный коэффициент, равный 0,8; - безразмерный коэффициент, равный 0,8;  - среднее значение вертикального нормального напряжения (далее - вертикальное напряжение) от внешней нагрузки в - среднее значение вертикального нормального напряжения (далее - вертикальное напряжение) от внешней нагрузки в  -м слое грунта по вертикали, проходящей через центр подошвы фундамента (см. 5.5.32), кПа; -м слое грунта по вертикали, проходящей через центр подошвы фундамента (см. 5.5.32), кПа;  - толщина - толщина 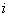 -го слоя грунта, см, принимаемая не более 0,4 ширины фундамента; -го слоя грунта, см, принимаемая не более 0,4 ширины фундамента; 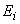 - модуль деформации - модуль деформации 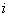 -го слоя грунта по ветви первичного нагружения, кПа; -го слоя грунта по ветви первичного нагружения, кПа;  - среднее значение вертикального напряжения в - среднее значение вертикального напряжения в 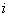 -м слое грунта по вертикали, проходящей через центр подошвы фундамента, от собственного веса выбранного при отрывке котлована грунта (см. 5.5.33), кПа; -м слое грунта по вертикали, проходящей через центр подошвы фундамента, от собственного веса выбранного при отрывке котлована грунта (см. 5.5.33), кПа; 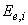 - деформации - деформации 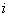 -го слоя грунта по ветви вторичного нагружения, кПа; -го слоя грунта по ветви вторичного нагружения, кПа; 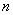 - число слоев, на которые разбита сжимаемая толща основания. - число слоев, на которые разбита сжимаемая толща основания. |
При отсутствии опытных определений 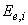 для сооружений II и III уровня ответственности допускается принимать
для сооружений II и III уровня ответственности допускается принимать  .
.
В формуле правое слагаемое вносит корректировку на величину осадки, связанную с тем, что после обустройства котлована при повторном нагружении грунты ведут себя иначе, чем образцы испытанные нагрузкой единожды в лаборатории.
В учебных заданиях принимается использовать более простую формулу для расчета осадки каждого слоя, выделенного в разрезе:
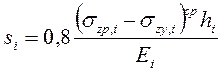 или
или 
Для вычисления общей осадки необходимо сложить осадку каждого слоя.
Вычисление осадки выполняют до границы сжимаемого слоя, на рис. 2.2 это линия ВС.
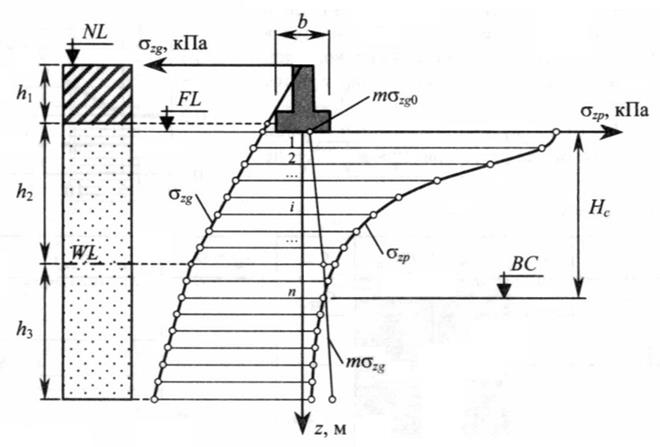 |
| Рис. 2.2. Общий вид схемы расчета |
Нижняя граница сжимаемой толщи определяется с учетом геологического строения и формы фундамента. В случаях, когда на незначительных глубинах залегают плохо сжимаемые грунты (скальные и полускальные грунты) за нижнюю границу сжимаемой толщи принимают кровлю этих грунтов. В остальных случаях разбивку на элементарные однородные слои продолжают до глубины, где σzp = m* σzg. Коэффициент m удобнее определять по графику на рис.2.3 в зависимости от модуля деформации грунтов и ширины фундамента.
