Методом последовательных приближений

Оценка проектов полигонометрических сетей заключается в определении ожидаемых ошибок координат узловых пунктов, относительных ошибок ходов и сравнении их с допустимыми. Выполняется строгими и приближенными способами.

Строгая оценка, как правило, выполняется на ЭВМ по специальным программам, а приближенная - по соответствующим формулам.

Для оценки проектов полигонометрических сетей наиболее простым является методом последовательных приближений. Этот метод дает возможность подсчитать ожидаемую среднюю квадратическую ошибку определения положения каждой узловой точки по отношению к группе смежных узловых точек, а не по отношению к исходным пунктам.

Для начала оценки необходимо произвести линейные измерения. Для этого измеряются длины линий в ходах, сходящихся в узловых точках I и II. Вычисленные длины линий заносят в таблицу 5.

Таблица 5

№ хода	Число сторон в ходе	Длина хода, км

При отступлении от требований инструкций необходимо выполнить расчет точности измерений углов и линий.

В инструкции по построению геодезических сетей обоснования и сетей сгущения предусмотрены точные показатели угловых и линейных измерений во всех классах и разрядах построения. В инженерно-геодезических работах иногда возникает необходимость делать отступления от требований инструкций. Например, увеличить длину хода против максимальной допустимой инструкцией. Чтобы сохранить точность определения хода согласно инструкции, необходимо повысить точность измерения углов и линий в ходе. Может оказаться технически необходимым повысить точность съемочного геодезического обоснования на промышленно-заводской территории по сравнению с предусмотренной инструкцией при сохранении максимальных длин ходов рекомендованных этой инструкцией. Во всех перечисленных случаях возникает задача расчета допустимых длин полигонометрического хода при рассматриваемом варианте построения и расчеты требуемой точности измерений углов и линий. Для таких расчетов введем обозначение:

Т – знаменатель предельной допустимой относительной невязки хода;

Т_у – знаменатель средней относительной ошибки хода вызванной погрешностями в угловых и линейных измерениях;

Т_ср – знаменатель средней относительной невязки хода;

Т_л – знаменатель относительной точности линейных измерений.

Т_ср=2Т (13)

Если в основу расчетов взять принцип равных влияний ошибок линейных и угловых измерений, то

Т_у = Т_л = Т_ср √2 (14)

Значения допусков установленных инструкцией приведены в таблице 6.

Таблица 6

Разрядность построения полигонометрии	Предельная относительная невязка хода fs/Sпред	Т	Тср	Ту = Тл
4 класс I разряд II разряд	1:25000 1:10000 1:5000

В проектируемой полигонометрической сети особое внимание при расчетах уделяется нахождению ожидаемой ошибки определения положения узловых точек. Допустимая длина полигонометрического хода между узловой и исходными точками определяется формулой:

L_узл= М Т_ср √n (15)

Когда первичное геодезическое обоснование строится в виде сплошной сети полигонов, ошибка определения положения каждой узловой точки подсчитывается по отношению к смежным узловым точкам, которые также являются определяемыми, а, следовательно, в этом случае при оценке ожидаемой точности определения положения каждой узловой точки надо учитывать ошибки исходных данных. Если длины ходов полигонометрической сети сходящихся в узловых точках примерно одинаковы, то ожидаемую среднюю квадратическую ошибку положения каждой узловой точки по отношению к ближайшим узловым точкам рассчитывается:

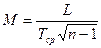(16)

где L – длина полигонометрического хода;

n – число ходов;

Т_ср – знаменатель средней относительной ошибки.

Периферийные пункты полигонометрической сети определяются менее точно, чем пункты средней сети. Для определения допустимой длины хода используется формула:

L= М Т_ср √n -1 (17)

При расчетах требуемой точности линейных измерений необходимо учитывать, что случайные ошибки измерений каждой линии в ходе являются независимыми и накопление их происходит пропорционально корню квадратному из количества линий в ходе.

Для подсчета требуемой точности линейных измерений в ходах с примерно равными длинами сторон, при наличии только случайных ошибок в результатах измерений применяется формула:

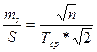(18)

где n – количество линий в ходе;

m_s – средняя квадратическая ошибка измерений линий;

S – длина линии.

Для расчета требуемой точности измерений углов в зависимости от разряда построения применяют формулу:

(19)

где n – количество сторон хода.

Для дальнейшей оценки необходимо произвести следующие расчеты. В первом приближении системы ходов рассматриваются как самостоятельные системы, все ходы которых идут от исходных пунктов А,Б, В, Г (рисунок 4), т. е. для системы ходов Z₁, Z₂ и Z₃ исходными пунктами будут точки А, Б и II, а для системы Z₃, Z₄ и Z₅ – точки В, Г и I.

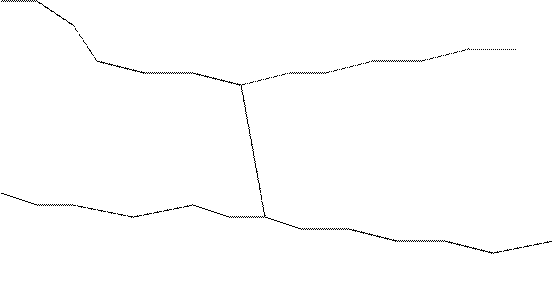
Рисунок 4 – Система ходов

Ожидаемые ошибки определения конечных точек каждого хода вычисляют по формуле:

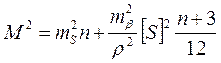(20)

где n – количество линий в ходе;

[S] – длина хода;

m_S - средняя квадратическая ошибка измерения линии;

m_β - средняя квадратическая ошибка измерения угла.

Вычисленные средние ожидаемые ошибки определения положения конечных точек хода по формуле (20) записывают в таблицу 7.

Таблица 7

№ хода			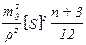М2	М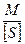
Z1
Z2
Z3
Z4
Z5

Веса определения положения узловых точек I и II по соответствующим ходам Z₁, Z₂ и Z₃; Z₃, Z₄ и Z₅ вычисляются по формулам:

для I узловой точки:

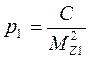
для II узловой точки: (21)

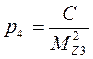
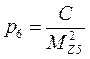
где С – постоянная величина и равна 100000.

Общий вес определения положения узловых точек I и II будет

Р₁= Р₁ +Р₂+ Р₃; Р₂ =Р₃ +Р₄₊ Р₅

Средние квадратические ошибки определятся формулой:

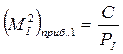
(22)

º

Во втором приближении полученные средние квадратические ошибки узловых точек I и II по формуле (22) в первом приближении следует учесть как ошибки исходных данных. Тогда для узловой точки I получим

М_Z1, M_Z2, М _Z3=√M²_Z3+(M₁)² _{1 прибл.}

Веса по ходам во втором приближении будут

Р₁, Р₂, Р₃; (Р₁)_{2 прибл.,} (М₁)²_{1 прибл.}

Для второй узловой точки:

М_Z3=√M²_Z3+(M_II)²₁ прибл., (M_II)_{2 прибл.};

Р_Z3, Р_Z4, Р_Z5, (P_II)_{2 прибл.}, (М_II)_{2 прибл.}

В третьем приближении в качестве ошибок исходных данных принимают ошибки определения положения узловых точек I и II, полученных во втором приближении, и т.д.

Приближения продолжают до тех пор, пока в двух последних приближениях будут получены практически одинаковые средние квадратические ошибки. Обычно даже в весьма сложных сетях с большим количеством узловых точек достаточно ограничиться тремя приближениями.

В больших полигонометрических сетях оценкой способом последовательных приближений будут получены величины ошибок определения узловых точек по отношению к группе смежных узловых точек, а не по отношению к удаленным от оцениваемых узловых точек исходным пунктам.

Если пункты расположены на краях обширной однородной по построению полигонометрической сети, то по мере удаления от исходных пунктов к середине сети величины ожидаемых ошибок определения положений узловых точек не будут возрастать. На участках, где узловые точки образуются более короткими ходами, они будут, наоборот, уменьшаться.

После выполнения оценки необходимо убедиться, что проект сети удовлетворяет точностным требованиям. Для этого по каждому ходу необходимо подсчитать величины влияния предвычисленных ошибок узловых точек, пользуясь формулой:

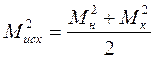(23)

Общая ожидаемая ошибка по ходу определяется формулой:

М²_об= М²_исх+ М²_Z (24)

где М_н, М_к – ожидаемые ошибки определения положения начальной и конечной точек хода;

М_Z – ошибка, накопленная в результате действия ошибок измерения углов и линий в ходе, вычисляемая по формуле 4.

Затем вычисляют среднюю квадратическую относительную ошибку 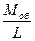и предельную относительную ожидаемую ошибку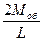

Ниже приводится пример оценки проекта сети (рисунок 4) методом последовательных приближений.

Сеть относится к полигонометрии I разряда. Измерение линий предполагается произвести светодальномером, поэтому средняя квадратическая ошибка измерения линий принята m_S =±20 мм, а ошибка угла m_β=±5'',0

Число линий в ходах и длины ходов, а также ожидаемые ошибки М², вычисленные по формуле 4 приведены в таблицах 8-9.

Таблица 8

№ хода	Число сторон в ходе	Длина хода, км
Z1		1,4
Z2		2,5
Z3		1,6
Z4		1,8
Z5		1,2

Таблица 9 – Вычисление средних ожидаемых ошибок определения положения конечных точек хода

№ хода		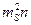	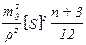М2	М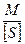
Z1					1:29500
Z2					1:28000
Z3					1:29600
Z4					1:29500
Z5					1:25700

Оценка проекта сети приведена в таблице 10

Таблица 10 – Вычисление средних квадратических ошибок узловых точек I и II

№ хода

№ исходной точки

I приближение

II приближение

III приближение

Mz

Mисх.

М2z

M2исх.

Mоб.

P

Mz

Mисх.

М2z

M2исх.

Mоб.

P

Mz

Mисх.

М2z

M2исх.

Mоб.

P

I узловая точка

Z1 Z2 Z3

А В II

Σ Р= 90 М2=1100, М=33

Σ Р= 82 М2=1220, М=35

Σ Р= 82 М2=1220, М=35

II узловая точка

Z3 Z4 Z5

I D C

Σ Р= 106 М2=940, М=31

Σ Р=97 М2=1030, М=32

Σ Р= 97 М2=1030, М=32

Вычисления предельной относительной ожидаемой ошибки приведены в таблице 11

Таблица 11 – Вычисление предельной относительной невязки хода

№ хода	Длина хода в км, L	Номера точек	М2н	М2к	М2исх	М2z	М2об	Моб, км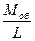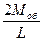
начальная	конечная
Z1 Z2 Z3 Z4 Z5	1,4 2,5 1,6 1,8 1,2	А В I D C	I I II II II							1:26000 1:27000 1:25000 1:28000 1:23000	1:13000 1:13500 1:12500 1:14000 1:11500

Как видно из таблицы 11 рассчитанные относительные ошибки по всем ходам укладываются в допуски, установленные для полигонометрической сети I разряда (таблица 5).

При коротких ходах в оцениваемой схеме полигонометрической сети относительные предельные ошибки могут оказаться больше допустимых. В этом случае точность проекта считается достаточной, если абсолютные величины ошибок определения положения узловых точек меньше 50 мм.

После проведения всех вычислений делается заключение о запроектированной сети.

СПИСОК ЛИТЕРАТУРЫ

1 Инструкция по построению государственной геодезической сети. Геодиздат, 1981

2 Практикум по курсу прикладной геодезии. Москва: «Недра», 1977

3 Справочное пособие по рекогносцировке пунктов триангуляции и полигонометрии. Москва: «Недра», 1975

4 Судаков С.Г. Основные геодезические сети. Москва: «Недра», 1975

5 Инструкция по полигонометрии и трилатерации. Москва: «Недра», 1976.

6 Лебедев Н.Н. Курс инженерной геодезии. Геодезические работы при проектировании и строительстве городов и тоннелей. Москва: «Недра», 1974

Н

7 Справочник по инженерной геодезии. Под ред. Н.Г. Видуева. Киев: «ВИЩА ШКОЛА», 1978

Приложение А

Величины 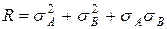(в единицах шестого знака логарифма)

10º

12º

14º

16º

18º

20º

22º

24º

26º

28º

30º

35º

40º

45º

50º

55º

60º

65º

70º

75º

80º

85º

90º

20º

30º

50º

70º

90º

115º

Продолжение приложения А

135º

152º