ЖердіҢ пішіні мен кӨлемі туралы тҮсінік.

Лекция 2

Т а р а у ЖЕР БЕТІНДЕГІ НҮКТЕЛЕРДІҢ ОРНЫН АНЫҢТАУ.

ЖЕРДІҢ ПІШІНІ МЕН КӨЛЕМІ ТУРАЛЫ ТҮСІНІК.

Жердің пішіні мен көлемін зерттеу жер бетін картада дұрыс кескіндеуте мүмкіндік туғызады және ол ғылым мен техниканың көптеген міндеттерін шешу (жасанды серіктерді және ғарыш кемелерін ұшыру, теңізде жүзу, авиация, радиобайланыс және т. б.) үшін кажет.

Жердің физикалық бетінің жалпы ауданы 510 млн км²-қа тең және геометрия жағынан алғанда пішіні күрделі. Орасан кеңістікті (жер бетінің 71 %-ін) мұхиттар мен теңіз шұңқырлары алып жатыр, олардың тереңдігі 11000 м-ге дейін жетеді. Дүниежүзілік мұхиттың орташа терендігі — 3800 м-ге жуық. Құрлықта тау жоталары, шатқалдар, жазықтар, өзен алқаптары және жыра, сайлар бар. Кейбір таулардың, мәселен, Эверестің (Джомолунгма) биіктігі 9000 м-ге жуық. Құрлыктың теңіз деңгейінен орташа биіктігі 875 м-ге тең. Сонымен, құрлықтың көлемі дүниежүзілік мұхитқа қарағанда аз ауданды алып жатқандықтан, сондай-ақ кұрлықтың мұхит тереңіндегі қыраттармен салыстырғанда онша биік болмайтындықтан, мұхит деңгейін жердің фигурасы ретінде қабылдауымыз кажет.

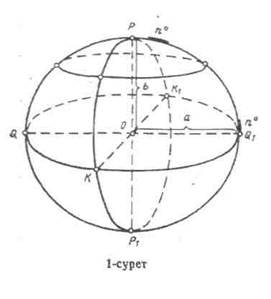
Егер де бүкіл планета материктер астымен үздіксіз жалғасып жататын дүниежүзілік мұхит бетінің тынық кезіндегі жағдайымен шектелген десек, тұтас алғанда жердің пішіні туралы түсінік алуға болады. Осындай тұйық бет өзінің әрбір нүктесінде вертикаль бағытқа, яғни ауырлық күшінің бағытына перпеидикуляр болады, ал ол деңгейлік бет деп аталады. Осы деңгейлік бетпен шектелген денені геоид дейді. Геоид — толқын мен ағынның жоқ кезінде мұхиттардағы судың орта деңгейі мен материктегі мұхитпен жалғасқан шартты түрде алынатын су деңгейінің фигурасы. Салмақ күші деңгей бетінің потенциалы болып табылатын геоид жер фигурасы деп есептелінеді. Геоид пішіні күрделі, дегенмен осы фигура жалпы сфероидқа, яғни -Р1Q Р1Q (І-сурет) эллипстің кіші осі РР1 теңірегінде айналуынан шығатын айналу эллипсоидына жақын. Сфероид бетін РР1 айналу осі арқылы өтетін жазықтықтармен қиғанда меридиандар деп аталатын эллипстер (РКР1К1) пайда болады. РР1 айналу осіне перпендикуляр жазықтық қималар параллель шеңберлерін түзеді. Сфероидтың центрі (О) арқылы өтетін жазықтық параллель QKQ1 K экватор деп аталады. Экватордың О Q1=а радиусы және ОР=b кесіндісі сфероидтың үлкен және кіші жар-тылай осьтерін құрайды. ά=(а— b)/а шамасы сфероидтың сығылушылығы деп аталады. а, b және ά шамаларын градустық өлшеулер арқылы анықтауға болады, ол үшін меридиан доғасының ұзындығын әрбір 1° сайын өлшеу керек. Меридианның әр түрлі жеріндегі градустың ұзындығын біле отырып, жердің пішіні мен көлемін анықтауға болады.

Жердің фигурасына мейлінше жақын келетін эллипсоидты жер эллипсоиды деп атайды. Жер эллипсоидының көлемдерін анықтау үшін жер бетінің барлық жерінде геодезиялық өлшеулер жүргізілуге тиіс. Әзірше мұндай өлшеулер толық жүргізіл-мегендіктен, жер эллипсоидының дәл параметрлерін анықтауға мүмкіндік болмай отыр. Осы орайда кейбір елдерде геодезиялық өлшеулерді өңдеу барысында геодезиялық жұмыстардың нәтижелері бойынша шығарылған өз эллипсоидтары қолданылады; олар сол елдің немесе бірнеше елдің территориясын толық, не ішінара қамтиды. Осындай эллипсоид референц-эллипсоид деп аталады. Референц-эллипсоид дегеніміз нақты бір елде геодезиялық өлшеулерді өңдеу үшін қолданылатын, жер денесінде белгілі түрде бағдарланған, нақты көлемі анықталған ЭЛЛИПСОИД.

Жер эллипсоидының көлемін әлденеше рет әр түрлі елдердің ғалымдары анықтады. 1946 жылға дейін ТМД-да 1841 жылы неміс ғалымы Ф. В. Бессель есептеп шығарған жер эллипсоидының көлемі қолданылды (а=6377 397 м, b=6356079 м, ά =1: 299,2). 1945 жылдан бастап геодезиялық жэне картографиялық жүмыстар үшін Ф. Н. Красовскийдің референц-эллипсоидының мынадай көлемдері бекітілді: а=6378245 м, b = 6356863 м, ά=1:298,3. Батыс Европанын және АҚЩ-тың гравиметриялық және астрономиялық материалдарынын реттеудеуден алынған градустық өлшеулері осы эллипсоидтың көлемдері қолданылған материалдардан аумағы жағынанда, оларды өңдеудің дәлме-дәлдігі жағынан да неғүрлым басымырақ болып табылады.

Көптеген есептерді шығарғанда сфероид сығылушылығының аз (ά =1 : 300) болғандығынан жердің фигурасы үшін радиусы 6371,11 км сфераны қолдануға болады. Кейбір жағдайларда,жер учаскелерінің ұзындықтары 20—30 км-ден аспаған кезде, жердің сфералылығын елемеуге де болады.