Іформаційні основи обчислювальної техніки

Інформація та її природа

Одне з найважливіших положень в кібірнетиці полягає в тому, що без інформації та її переробки неможливо організувати системи, якими є живі організми та штучні, создані людиною, керовані системою.

У повсякденному житті інформацією ми називаємо різні сведінія о явищах природи, події в суспільному житті та процесах у технічних системах. Інформація міститься в мові людей, текстах книг, колонках цифр і на ряду з цим у показниках годинників, термометрів, вольтметрів.

В обчислювальній техніці інформація – властивість об’єктів і явищ ( процесів ) породжувати багатообразний стан, яке за допомогою відображення передачі від одного об’єкта до іншого та запечетліваются у його структурі ( можливо в зміненому вигляді ). При цьому не самі об’єкти та явища є інформацією, а їх віддзеркалення у вигляді чисел, формул, описів, креслень, символів та інших абстрактних характеристик, тобто годинники, формули, тексти, мови – не є інформацією, а лише її носії. Сама по собі інформація може бути віднесена до області абстрактних категорій.

Формули та - носії інформації про поведінку матеріальної точки.

Передача інформації (перенесення її на відстань ) передбачає наявність, як мінімум двох об’єктів – джерела інформацій та приймача інформації. Для передачи інформації стан джерела представляється у зовнішньому середовищі в матеріально енергетичній формі за допомогою безлічі станів деяких матеріальних об’єктів, називається показником інформації, або сигналом. Розрізняють сигнали : видимі ( TV зображення ), звукові ( звонок ), електричні ( + або - ) та інші. Одні сигнали можуть викликати інші :

електричний сигнал → звонок → звуковий сигнал

світловий → фотодіод → електричний сигнал

Відображення безлічі станів джерела у множину станів носія інформації називається кодуванням, а відображення безлічі станів носія у множину станів приймача – декодуванням. Образ стану джерела при вибраному способі кодування називається кодом цього стану.

Інформація втілена та закодована в деякій матеріальній формі, називається повідомленням. Повідомленнями можуть бути, наприклад, розподілення яскравості на поверхні передаваймого об’єкта, а також розподілення яскравості на екрані TV при відтворенні об’єкта.

Узагальнена модель системи передачи інформації

Середовище : повітря, дроти, світловий промінь (оптична), рідина (гідравлічна)

Приклад : скрипаль в студії → слухачь

Первинний перетворювач → мікрофон; через посилювач та модулятор (coder; код-ноти) на передавач. По каналу зв’язку інформація поступає на приймач, після чого за допомогою елементів слуху та емоційного сприйняття потрапляє до адресата.

Форми уяви інформації

Джерело інформацій та створювані ним повідомлення та сигнали розділяють на непреривну та дискретну.

Якщо сигнал (повідомлення) в кінцевому інтервалі амлітуд приймає довільну кількість значень, то він (вона) називається непреривним ; якщо кількість значень обмежене, то сигнал (повідомлення) – дискретне.

Непреривні повідомлення відображаються сигналами, відображаючими собою якісь фізичні величини, змінні непреривно та приймаючі нескінченне число значень в деяких діапазонах. Така форма уявлення інформації використовується в аналогових і обчислювальних пристроях. ( сигнали в аналогових пристроях, вимір маси тіла, відстань між двома точками, напруга електричного току, проміжок часу між двома подіями, відхилення стрілки барометра при вимірі тиску, зміна току в телефонній слухалці).

Дискретні повідомлення складаються з скінченної множени елементів ( скінченного числа значень ), які формуються джерелом інформації та називаються літерами, або символами. Літери відображаються сигналами, приймаючими кінцеве число значень. В інформаційній та обчислювальній техніці поняття літери включає в себе символи різних систем письма, цифри, пунктуаційні знаки, математичні символи та інші. Якщо елементам дискретного повідомлення поставленні у відповідность цифри або деяки їх сукупності, та така перестановка інформації називається цифровим (числовим). Кінцевий набір букв складає алфавіт.

Дискретні сигнали як засіб передачі інформації знайшли більш широке застосування, ніж непреривні, так як вони менш схильні впливу перешкод в каналах зв’язку. Можливість передачі непреривних повідомленнь за допомогою дискретних булла доведена В.А. Котельниковим в 1993 році :

Якщо функція непреривна та її частковий спектр не містить складаючих частин, перебільшуючих F гц , то вона цілком визначається сукупністю ординат, відстаючих у часі друг від друга на ½ F сек.

Одним з найбільших досягнень інженерної думки є те, що може бути дана кількісна оцінка: інформацію можна виміряти.

Виміри кількості інформації.

Деякі сведінія можуть містити в собі мало інформації, а інші багато. Існує низка засобів оцінки кількості інформацій, Але в техніці частіше використовують спосіб оцінки, запропонований в 1948 році французьким вченим Клодом Шенноном.

Пиклад :інформацію стосовно місця фігури на дошці для шахів можна отримати двома способами :

- кодування кожної з 64 клітинок в двійковій системі чисел потребує 6 елементів;

- кодування номерів 8 вертикалей та 8 горизонталей потребує 2 повідомлення по 3 елементи.

Кількість інформації, представлена двома способами, однакова.

Отримання інформації знищує невизначеність, ліквідує невідомість о факті передачі. Степінь невизначеності прийнято характеризувати поняттям ‘ймовірності’ – велечиною приймаючою значення в діапазоні від 0 до 1 і визначающою міру можливості в інших випадках. Якщо подія не може відбутисяніколи, то його ймовірність рівна нулю (‘завтра Земля прийме форму куба’).

Чим більша ймовірність події, Тим більша впевненість, що воно відбудеться, і Тим менше інформації містить повідомлення про цю подію. Повідомлення ‘Земля має форму кулі’, спрямоване вчителю географії, не містить інформації. Коли ймовірність події мала, повідомлення, що воно станеться, дуже інформативне, наприклад: ‘Під каракумськими пісками знаходиться велитенське озеро з прісною водою’.

Якщо об’єкт може знаходитися в одному з n різних станів, які позначаються числами 1,2,…., n і ці стани мають місце з верогітністю 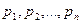відповідно, то кількість інформації I, характеризуючої стан, в якому перебуває об’єкт рівне:

, або в компактній формі

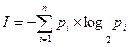
Слід помітити, що , тому двійкові логорифми ; якщо , то

,

Ця формула доволі складна для простого пояснення.

Скористуємся більш простою формулою, отриманою американським вченим Хартлі в 1928 році для наступного часного випадку:
Якщо об’єкт може знаходитись в одному з n станів і кожне з цих станів рівно ймовірне (тобто однаково можливе), то кількість інформації I, яка характеризує стан, в якому перебуває об’єкт, рівна .

Ця формула легко виводиться з більш загальної формули Шеннона, якщо в останню підставити однакові значення ймовірностей , рівні 1/n.

Використаємо формули Хартлі для оцінки кількості інформації в простих повідомленнях.

- Якщо об’єкт може знаходитися в одному з двох рівноймовірних станахт (наприклад, вийшовший з метро об’єкт може бути чоловіком або жінкою), то кількість інформації в повідомленні, визначаючому стан об’кта, рівна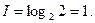

Одиниця інформації називається біт( bit – binary digit ) – кількість інформації, за допомогою якої виділяється один з двох рівноймовірних станів об’єкта.

- Якщо об’єкт може знаходитися в одному з 8 рівноймовірних станів, то 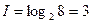біта.

- Якщо об’єкт може знаходитися в одному з 16 рівноймовірних станів, то біта.

- Яку кількість інформації містить один символ в тексті? Точно відповісти важко, так як необхідно знати частоту використання символів і різного роду сполучень символів в тексті.

Нехай текст будується на основі 64 символів, при чому частота використання різних символів однакова, тобто всі символи рівноймовірні. Кількість інформації в одному символі 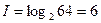біт.

З двох символів данного алфавіту можна утворити 64х64=4096 різних сполучень.

З цього випливає, що два символа містять в собі біт інформації.

- Оцінимо кількість інформації, яка міститься в числах. Якщо передбачити, що цифри 0,1,…,9 використовуються однаково часто, тобто усі 10 цифр рівноймовірні, то одна цифра містить 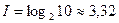біта інформації.

Чотирьохзначне число 0,1,…,9999 в передбаченні, що усі його значення рівноймовірні, містять біт інформації, а восьмизначне число при тій самій умові, містить 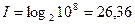біт інформації.

Вісім біт утворюють більш значущу одиницю виміру інформації – байт (byte) = 8 біт.

Для виміру великих об’ємів інформації використовують такі одиниці виміру:

- 1 кілобайт ;

- 1 мегабайт ;

- 1 гігабайт ;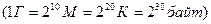

- 1 терабайт 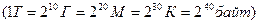.