Алгоритм идеальной работы автономных БИНС
УТВЕРЖДАЮ
Директор ЦНИИ «Электроприбор»
Академик РАН
В.Г. Пешехонов
"_____"__________________2013 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по проведению в учебном центре ЦНИИ «Электроприбор» лабораторной работы
Имитационное моделирование алгоритма работы бесплатформенной инерциальной навигационной системы
Санкт-Петербург
Цель работы
Целью данной работы является имитационное моделирование алгоритмов идеальной работы автономной бесплатформенной инерциальной навигационной системы (БИНС) и изучение влияния точностных характеристик ее чувствительных элементов на погрешность выработки кинематических параметров.
Целью работы является также ознакомление с методами нелинейного динамического моделирования в пакете Simulink.
Общие сведения
Сутьинерциального метода навигации заключается в интегрировании в реальном масштабе времени дифференциальных уравнений поступательного движения ц.м. подвижного объекта. В качестве исходной информации (первичных навигационных измерений) здесь используются измерения вектора кажущегося ускорения,которые осуществляются с помощью акселерометров. Системы, реализующие данный метод, принято называть инерциальными навигационными системами (ИНС).
Линейные акселерометры – это измерительные приборы, которые реагируют на линейное ускорение своего основания (корпуса) по отношению к свободно падающему телу и используются для измерения этого, т. е. кажущегося ускорения 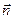 основания, на котором они установлены.
основания, на котором они установлены.
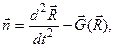 (1)
(1)
здесь 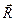 - радиус-вектор, определяющий положение корпуса прибора относительно ц.м. Земли;
- радиус-вектор, определяющий положение корпуса прибора относительно ц.м. Земли;
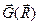 - удельная сила притяжения Земли в центре корпуса акселерометра и являющаяся функцией радиус-вектора
- удельная сила притяжения Земли в центре корпуса акселерометра и являющаяся функцией радиус-вектора 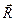 .
.
Уравнение (1) иногда называют основным уравнением инерциальной навигации, т.к. в его интегрировании и состоитсущность метода инерциальной навигации. Т.е. по измеренным составляющим вектора 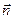 и априори известной зависимости
и априори известной зависимости 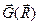 путем двойного интегрирования при известных начальных условиях и заданной или вычисленной ориентации измерительных осей акселерометров относительно навигационных осей можно определять линейную скорость и координаты местоположения подвижного объекта.
путем двойного интегрирования при известных начальных условиях и заданной или вычисленной ориентации измерительных осей акселерометров относительно навигационных осей можно определять линейную скорость и координаты местоположения подвижного объекта.
Задачей ИНС является выработка кинематических параметров движения объекта: как навигационных (характеризующих поступательное движение ц.м. объекта в низкочастотной области спектра), так и динамических (характеризующих высокочастотное угловое и линейное движение с учетом рыскания, качки и орбитального движения некоторой точки корабля относительно его ц.м.).
Алгоритм идеальной работы автономных БИНС
В состав БИНС входят инерциальный измерительный модуль (ИИМ), содержащий чувствительные элементы – акселерометры и гироскопы, и вычислитель, реализующий алгоритмы работы БИНС. При этом акселерометры вырабатывают первичную навигационную информацию (производят первичные навигационные измерения). Гироскопы в БИНС - три датчика угловой скорости (ДУС) типа лазерного, волоконно-оптического или микромеханического гироскопа используются для определения (вычисления) угловой ориентации блока акселерометров относительно выбранной навигационной системы координат.
Вырабатываемыми кинематическими параметрами (выходная информация вычислителя) являются:
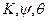 - углы курса, бортовой и килевой качки, определяющие ориентацию осей
- углы курса, бортовой и килевой качки, определяющие ориентацию осей 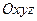 ИИМ БИНС относительно сопровождающего географического трехгранника
ИИМ БИНС относительно сопровождающего географического трехгранника 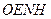 ;
;
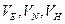 - восточная, северная и вертикальная составляющие линейной скорости объекта относительно Земли;
- восточная, северная и вертикальная составляющие линейной скорости объекта относительно Земли;
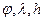 - широта, долгота и высота места объекта.
- широта, долгота и высота места объекта.
Первичными навигационными измерениями (исходной информацией для выработки выходных данных) ИИМ на ДУС являются:
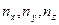 - составляющие вектора кажущегося ускорения
- составляющие вектора кажущегося ускорения 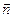 на оси
на оси 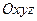 ИИМ;
ИИМ;
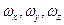 - составляющие вектора угловой скорости
- составляющие вектора угловой скорости 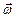 вращения трехгранника
вращения трехгранника 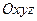 на свои оси.
на свои оси.
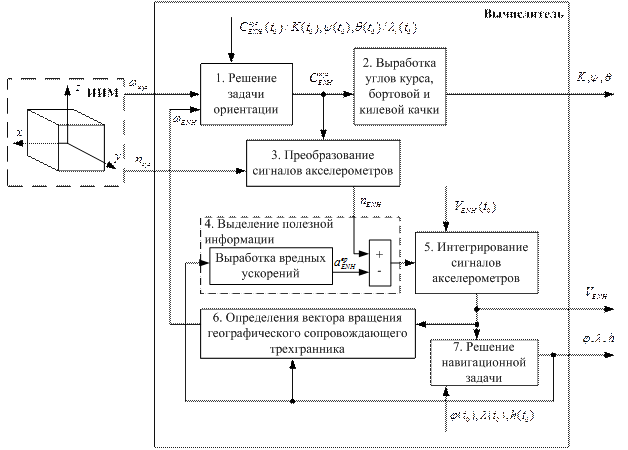
Рис. 1. Блок-схема алгоритма идеальной работы автономных БИНС
Блок-схема алгоритма идеальной работы автономных БИНС приведена на рис.1 и состоит из следующих блоков:
1. Решение задачи ориентации
Определение ориентации ИИМ БИНС, содержащего блок акселерометров, и подвижного объекта в целом относительно сопровождающего географического трехгранника с целью приведения сигналов акселерометров к осям навигационного сопровождающего трехгранника необходимой для последующего решения навигационной задачи. Ориентация объекта и блока акселерометров в частности задаётся матрицей направляющих косинусов, т.е. матрицей перехода от осей 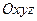 связанных с объектом (рис. 2) к географическим
связанных с объектом (рис. 2) к географическим 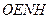 осям (рис. 3). Обычно оси ИИМ совпадают со связанными с объектом.
осям (рис. 3). Обычно оси ИИМ совпадают со связанными с объектом.
Задача ориентации решается с использованием данных блока гироскопов. В БИНС с ИИМ на ДУС - это интегрирование кинематических уравнений вращательного движения объекта с целью вычисления матрицы ориентации 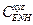
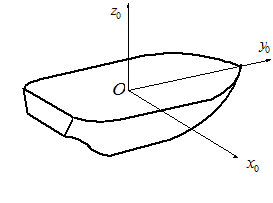 | 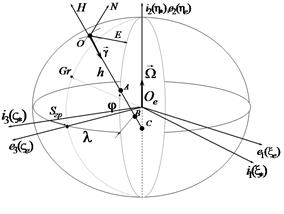 |
Рис.2. Система координат 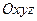 , связанная с корпусом объекта , связанная с корпусом объекта | Рис.3. Географический сопровождающий трехгранник 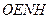 и инерциальная СК и инерциальная СК 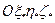 |
Кинематические уравнениясвязывают вектор 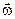 угловой скорости вращения объекта с производными по времени от параметров ориентации. Вид кинематических уравнений определяется в зависимости от кинематических параметров, поэтому для углов Эйлера-Крылова, направляющих косинусов, и параметров Родрига-Гамильтона уравнения различны. Для решения кинематических уравнений, как и для любых других дифференциальных уравнений, должны быть известны начальные условия, для чего решается задача начальной выставки.
угловой скорости вращения объекта с производными по времени от параметров ориентации. Вид кинематических уравнений определяется в зависимости от кинематических параметров, поэтому для углов Эйлера-Крылова, направляющих косинусов, и параметров Родрига-Гамильтона уравнения различны. Для решения кинематических уравнений, как и для любых других дифференциальных уравнений, должны быть известны начальные условия, для чего решается задача начальной выставки.
Для углов Эйлера-Крылова
Когда преобразование задается тремя последовательными плоскими поворотами на углы курса, килевой и бортовой качки 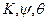 , то кинематические уравнения имеют следующий вид
, то кинематические уравнения имеют следующий вид
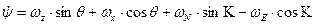 ,
,
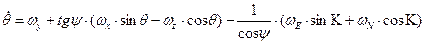 , (2)
, (2)
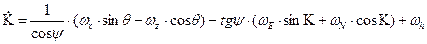 ,
,
где 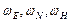 – проекции на свои оси угловой скорости вращения географического сопровождающего трехгранника
– проекции на свои оси угловой скорости вращения географического сопровождающего трехгранника 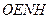 относительно инерциальной СК
относительно инерциальной СК 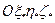 .
.
Матрица ориентации вычисляется следующим образом
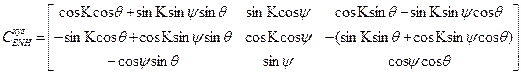 . (3)
. (3)
Для направляющих косинусов (уравнение Пуассона)
Если на борту подвижного объекта необходимо определять его ориентацию относительно системы координат, которая вращается в инерциальном пространстве, например, географического сопровождающего трехгранника 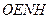 , тогда необходимо воспользоваться обобщенным уравнением Пуассона
, тогда необходимо воспользоваться обобщенным уравнением Пуассона
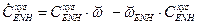 , (4)
, (4)
где 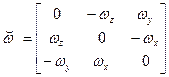 - кососимметрическая матрица, соответствующая вектору
- кососимметрическая матрица, соответствующая вектору 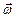 ;
;
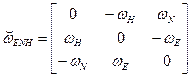 - кососимметрическая матрица, соответствующая вектору
- кососимметрическая матрица, соответствующая вектору 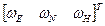 угловой скорости вращения географического сопровождающего трехгранника
угловой скорости вращения географического сопровождающего трехгранника 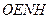 относительно инерциальной СК в проекции на свои оси.
относительно инерциальной СК в проекции на свои оси.
Для кватернионов
В кватернионной форме для кватерниона  осуществляющий переход от географического сопровождающего трехгранника
осуществляющий переход от географического сопровождающего трехгранника 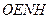 к связанному
к связанному 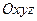 кинематические уравнения имеют вид
кинематические уравнения имеют вид
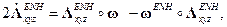 (5)
(5)
где 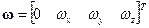 – гиперкомплексное отражение вектора
– гиперкомплексное отражение вектора 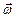 ;
;
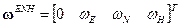 – гиперкомплексное отражение вектора
– гиперкомплексное отражение вектора 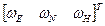 угловой скорости вращения географического сопровождающего трехгранника
угловой скорости вращения географического сопровождающего трехгранника 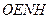 относительно инерциальной СК в проекции на свои оси.
относительно инерциальной СК в проекции на свои оси.
Или в матричной форме:
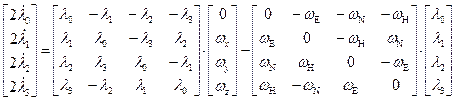 . (6)
. (6)
Матрица ориентации формируется по параметрам Родрига-Гамильтона следующим образом
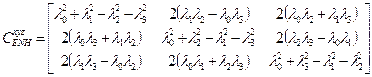 . (7)
. (7)
2. Выработка углов курса, бортовой и килевой качки
Если кинематические уравнения представлены в виде (4,5), то зная элементы матрицы ориентации 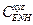 можно вычислить выходные параметры ориентации, т.е. углы
можно вычислить выходные параметры ориентации, т.е. углы 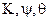 по следующим формулам:
по следующим формулам:
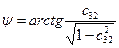 ,
, 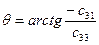 ,
, 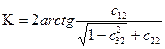 , (8)
, (8)
где 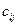 - элементы матрицы ориентации
- элементы матрицы ориентации 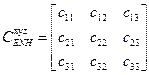 .
.
Поскольку модули углов 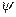 и
и 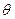 меньше 90º, то приведенные выше выражения однозначно определяют значения углов килевой и бортовой качек. Внутри диапазона от 0 до 360º функция
меньше 90º, то приведенные выше выражения однозначно определяют значения углов килевой и бортовой качек. Внутри диапазона от 0 до 360º функция 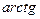 разрывов не имеет и однозначно определяет значение угла
разрывов не имеет и однозначно определяет значение угла 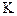 .
.
3. Преобразование сигналов акселерометров
Используя решение задачи ориентации, значения вектора 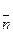 кажущегося ускорения, измеряемого блоком акселерометров в осях ИИМ, преобразуются к осям географического сопровождающего трехгранника
кажущегося ускорения, измеряемого блоком акселерометров в осях ИИМ, преобразуются к осям географического сопровождающего трехгранника 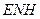 следующим образом
следующим образом
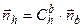 . (9)
. (9)
4. Выделение из сигналов акселерометров полезной информации
Так как задача навигации подвижного объекта решается вблизи поверхности Земли, то из сигналов акселерометров 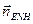 , приведенных к осям географического сопровождающего трехгранника, необходимо исключить так называемые "вредные" ускорения, определяющие кориолисово и переносное ускорения ц.м. объекта или точнее точки расположения блока акселерометров на объекте, а также составляющие вектора
, приведенных к осям географического сопровождающего трехгранника, необходимо исключить так называемые "вредные" ускорения, определяющие кориолисово и переносное ускорения ц.м. объекта или точнее точки расположения блока акселерометров на объекте, а также составляющие вектора 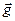 ускорения силы тяжести.
ускорения силы тяжести.
Значения "вредных" 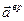 ускорений формируются в вычислителе БИНС по данным, вырабатываемым самой БИНС, и априорным данным о параметрах Земли: форме, размерах и угловой скорости вращения, по следующим формулам:
ускорений формируются в вычислителе БИНС по данным, вырабатываемым самой БИНС, и априорным данным о параметрах Земли: форме, размерах и угловой скорости вращения, по следующим формулам:
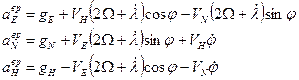 (10)
(10)
Для формирования модельных значений вектора 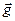 необходимо располагать соответствующей моделью гравитационного поля Земли:
необходимо располагать соответствующей моделью гравитационного поля Земли:
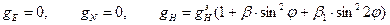 , (11)
, (11)
где 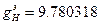 м/с2, для параметров эллипсоида Красовского: b=0.0053171, b1=0.0000071.
м/с2, для параметров эллипсоида Красовского: b=0.0053171, b1=0.0000071.
5. Интегрирование сигналов акселерометров,
Сигналы акселерометров «очищенных» от «вредных» ускорений интегрируются с привлечением начальных условий о составляющих вектора линейной скорости объекта в навигационных осях:
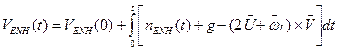 (12)
(12)
6. Вычисление текущих значений составляющих 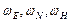
вектора угловой скорости вращения географического сопровождающего трехгранника 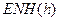 по данным о составляющих вектора линейной скорости объекта в навигационных осях, радиусах кривизны нормальных сечений и широте места для формирования обратной связи в задачу ориентации.
по данным о составляющих вектора линейной скорости объекта в навигационных осях, радиусах кривизны нормальных сечений и широте места для формирования обратной связи в задачу ориентации.
Составляющие 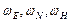 определяются соотношениями
определяются соотношениями
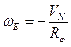 ,
, 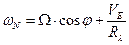 ,
, 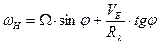 , (13)
, (13)
где 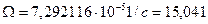 °/ч - угловая скорость суточного вращения Земли.
°/ч - угловая скорость суточного вращения Земли.
Радиусы кривизны нормальных сечений:
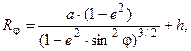
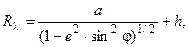 (14)
(14)
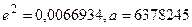 м – параметры эллипсоида Красовского.
м – параметры эллипсоида Красовского.
7. Решение навигационной задачи
Интегрирование составляющих вектора линейной скорости объекта в навигационных осях с привлечением начальных условий о координатах места объекта
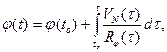
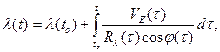 (15)
(15)
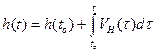 .
.
