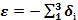Редукція довжин геод.ліній на пл-ні в пр. Г-К

Відомо, що на поверхні еліпсоїда віддаль між точками визначається довжиною геод.лінії, що з’єднує ці точки.Для випадку побудови геод.мереж на земн.пов-ні, де сторони менше 200 км, геод.лінію при розгляді цього питання можна замінити дугою нормального січення. При створенні плоского зображ.в пр.Г-К ця дуга норм.перер. відобразиться кривою, що буде на пл-ні утворювати з хордою кути δ, які наз.поправками в напрямок за кривину зображення геод.лінії на пл.-ні в пр..Г-К. При розгляді питання визначення віддалі між точками на пл.-ні в пр..Г-К за відомою довжиною геод.лінії на пов-ні еліпсоїда вплив цих кутів є незначним і тому його враховувати не будемо.Тоді залежність між дугою геод.лінії на еліпсоїді і відпов. Відрізком довжини на пл.-ні в пр..Г-К встановимо на основі ф-ли м-бу довжин: 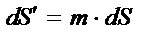(1)

Або з урахуванням іншої відомої ф-ли:

Звідси знайдемо:

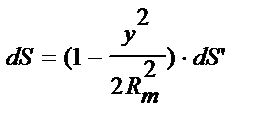
Інтегруємо цей вираз:

(2)

Нехай ми маємо площину в проект.Г-К.

В ф-лі (2) у означає поточну ординату лінії АВ, яка при інтегруванні може приймати різні значення в границях від у1 до у2.

Замінимо цю поточну ординату наступним чином:

у=у1+Δу

α – дирекційний кут

d – поточна відстань

А тоді з геодезії відомо:

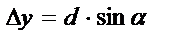
тоді

Підставимо цю частину в (2):

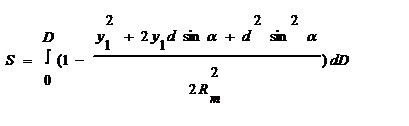в отриманому виразі ми отримали ряд елементів, які залежать і не залежать від D.

Інтегруємо отриманий вираз, знаючи, що інтеграл суми дорівнює сумі інтегралів:

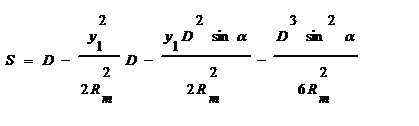
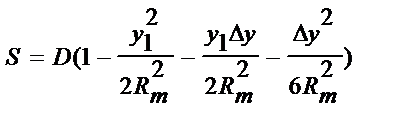(3)

Зробимо заміну в (3) ввівши середню ординату

Підставимо цю заміну в (3):

(4)

З формули (4) знаходимо формулу для визначення довжини лінії на площині в проек.Г-К. за відомою довжиною лінії на вихідній поверхні, тоді:

(5)

Ф-ла (5) є тою ф-лою, яка дозволяє визначити редуковане значення довжини геодезичної лінії S на площині в проекції Г-К.

Поправка в напр. за кривину зобр. геод. лінії

Геод. лінія – крива,в кожній точці якої нормаль до пов-ні еліпсоїда розміщується в дотичній пл.-ні до цієї поверхні. Геод.лінія на поверхні еліпсоїда з’єднує ті чи інші точки еліпсоїда по найкоротшій відстані. На цій пов-ні геод. лінія є складною кривою,що має і кривину і кручення.

Еліпсоїд

Q₁₀ Q₁

Q₂₀ Q₂

Пр-ція Г-К

Q₂₀´ y₂ Q₂´

∆ x δ₂₁

y₁ δ₁₂

Q₁₀´ Q₁´

Кути, що утворилися – δ наз. Поправками в напрямок за кривину зображ геод.лінії. Утвор на пов еліпсоїда чотирикутника,сума внутрішніх кутів = 360+ε, де ε – сфер.надлишок. На пр..Г-К в границях зони паралелі можна вваж перпендик до ос.мер-на. Сума внутрішніх кутів в чотир-ку Q’₁,Q’₂,Q’₁₀,Q’₂₀ буде: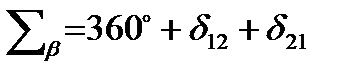

В теорії розвязку сферичних трик-ків за теоремою Лежандра доводиться що

Де P-площа відповідної фігури, R- сер радіус кривизни еліпсоїда для фігури. Прирівняючи:

Положення точок задається зон. К-ми, за якими можна визначити площу фігури як трапеції:

Підставимо у формулу :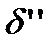

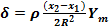
(2)- формула для кутів 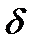є приблизною ф-лою яку можна використати при обробці геод мереж не вище 3-го класу точності.

Нехай точки Q₁ Q₂ є довільними точками на пл.-ні в пр.-ції Г-К. З’єднаємо їх хордою, яку приймемо за вісь ξ локальної с-ми к-т. Вісь η направлена перпендикулярна до неї. Елементарний відрізок dξ відповідає такому ж відрізку на геод. лінії що з’єднує ці точки. ρ – радіус цього елементарного відрізка. Приймемо елементарну дугу геод. лінії за дугу кола радіусом ρ:

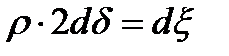; (3) З диф геометрії відома ф-ла для визн радіуса кривини довільних кривих:

Розглянемо утворений елементарний ∆ як плоский: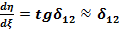

Оскільки вел-на мала, -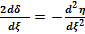

Після перетворень отримаєм:

Тоді: . (1)Для подальшого перетворенння використаєм зон с-му к-т. Задамо напрямок Q₁, Q₂ дир кута 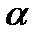,тоді довільна координата на цій лінії: y =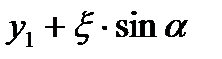

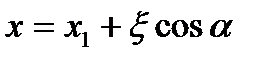
Продиф 1-ше р-ня:

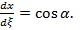Підставимо в (1), інтегруємо:

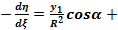
Визначимо зн-ня постійних інтегрування С₁,С₂.Нехай 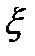=0, =0 Для цих р-нь:

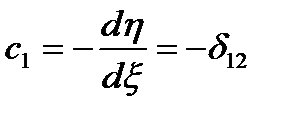
2-ге р-ння формули (6) буде

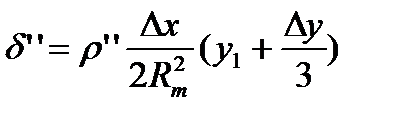-точна формула для визначення поправок за кривину зобр. геод. лінії на пл-ні в пр-ції Г-К.

В

А

ав

β β₀

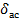С

Поправки за кривину зобр. геод. лінії у відповідний кут позначимо δ_i:

Тоді: 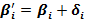.Якщо просумувати ці р-ня для всіх кутів трик-ка, то буде контр.вираз:

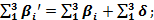
Звідси: