Определение электродвижущей силы источника тока методом компенсации
Цель работы: измерить электродвижущую силу источника тока методом компенсации.
Приборы и оборудования: установка для измерения электродвижущей силы источника тока методом компенсации.
Теоретическое сведение
Электрическим током называют направленное движение электрических зарядов. Электрический ток принято характеризовать силой тока 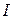 – скалярной величиной, определяемой электрическими зарядами
– скалярной величиной, определяемой электрическими зарядами 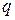 , проходящими через поперечное сечение проводника за единицу времени
, проходящими через поперечное сечение проводника за единицу времени 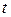 :
:
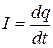 . (1)
. (1)
Единица измерения силы тока – ампер (А). Если за любые равные промежутки времени через поперечное сечение проводника проходит одинаковое количество электричества (электрический заряд), то такой ток называют постоянным. Условно за направление электрического тока в проводнике принимают направление движения положительных зарядов (рис. 1а).
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника 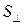 , перпендикулярного направлению тока, называется плотностью тока
, перпендикулярного направлению тока, называется плотностью тока 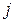 :
:
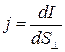 . (2)
. (2)
Плотность тока является вектором 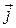 , направление которого совпадает с упорядоченным движением положительных зарядов.
, направление которого совпадает с упорядоченным движением положительных зарядов.
В 1826 г. экспериментально установлен закон Ома для однородного участка электрической цепи (эл. схема на рис. 1б или участки ad, dc, cb на рис.1а ), который гласит, что сила тока в однородном проводнике прямо пропорциональна напряжению 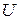 на его концах и обратно пропорциональна сопротивлению проводника
на его концах и обратно пропорциональна сопротивлению проводника 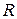 :
:
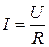 , (3)
, (3)
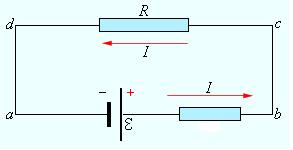 |  |  |
| а | б | в |
| Рис. 1. |
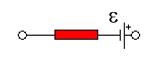
Сопротивление проводника зависит от материала, из которого изготовлен проводник, его линейных размеров и формы:
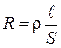 , (4)
, (4)
где 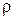 - удельное электрическое сопротивление, характеризующий материал проводника;
- удельное электрическое сопротивление, характеризующий материал проводника; 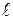 - длина проводника;
- длина проводника; 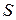 - площадь поперечного сечения проводника. Единица измерения удельного электрического сопротивления – Ом∙м. 1 Ом·м - это удельное электрическое сопротивление проводника, имеющего электрическое сопротивление 1Oм при длине 1м и площади поперечного сечения 1м2.
- площадь поперечного сечения проводника. Единица измерения удельного электрического сопротивления – Ом∙м. 1 Ом·м - это удельное электрическое сопротивление проводника, имеющего электрическое сопротивление 1Oм при длине 1м и площади поперечного сечения 1м2.
Если в выражение (4) подставить в закон Ома для однородного участка электрической цепи (3), то получим
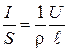 . (5)
. (5)
Учитывая, что
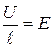 и
и 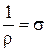 ,
,
а также применив формулу (2), уравнение (5) преобразуем в выражение, которое представляет собой закон Ома в дифференциальной форме для однородного участка электрической цепи:
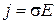 ,
,
где 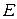 - напряженность электростатического поля внутри проводника;
- напряженность электростатического поля внутри проводника; 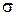 - удельная электрическая проводимость материала проводника.
- удельная электрическая проводимость материала проводника.
В виду того, что носители положительного заряда в каждой точке движутся в направлении вектора 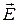 , то направления векторов
, то направления векторов 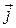 и
и 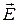 совпадают. Поэтому закон Ома для однородного участка электрической цепи в дифференциальном виде запишется как
совпадают. Поэтому закон Ома для однородного участка электрической цепи в дифференциальном виде запишется как
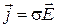 .
.
Для того, чтобы поддерживать ток в проводнике достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители заряда считаем положительными) непрерывно отводить приносимые положительные заряды, а к концу с большим потенциалом непрерывно их подводить, т.е. необходимо установить круговорот положительных зарядов, при котором они двигались бы по замкнутой траектории.
В замкнутой электрической цепи есть участки, на которых положительные заряды движутся в сторону возрастания потенциала, т.е. против электростатического поля. Перемещение таких зарядов возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними. Природа сторонних сил различная, т.к. их появление обусловлено переменными магнитными полями, а также химическими, диффузионными, световыми процессами, происходящими в источниках тока.
Основной характеристикой сторонних сил является их электродвижущая сила (ЭДС) – это физическая величина, численно равная работе сторонних сил 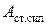 по перемещению единичного положительного заряда
по перемещению единичного положительного заряда 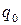 :
:
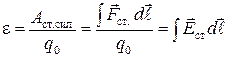 ,
,
где 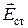 - вектор напряженности поля сторонних сил;
- вектор напряженности поля сторонних сил; 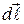 - вектор перемещения заряда. Единица измерения ЭДС - В (Вольт).
- вектор перемещения заряда. Единица измерения ЭДС - В (Вольт).
Если источник тока замкнуть на внешнюю нагрузку, равномерно распределенную по контуру, то потенциал будет падать по линейному закону по мере удаления от положительного электрода батареи (рис. 2).
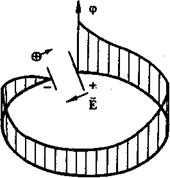
Рис. 2
Превращение энергии электрического тока во внутреннюю вызывает нагревание проводника. Дж. Джоуль и Э. Ленц экспериментально установили, что количество тепла, выделяющегося в проводнике, пропорционально квадрату силы тока в проводнике 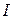 , сопротивлению проводника
, сопротивлению проводника 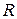 и времени течения тока
и времени течения тока 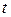 .
.
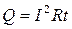 . (6)
. (6)
Используя закон Джоуля-Ленца, выведен закон Ома для неоднородного участка электрической цепи, в котором учтено действие электростатических и сторонних сил на движущийся положительный заряд.
Согласно закону сохранения энергии количество тепла, выделенного в неоднородной электрической цепи (эл. схема на рис. 1в), равно сумме работы сил электрического поля и работы сторонних сил источника тока:
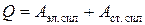 , (7)
, (7)
где 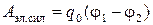 - работа сил электростатического поля;
- работа сил электростатического поля; 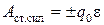 - работа сторонних сил. Сторонние силы совершают положительную работу по перемещению положительного заряда, если направления сторонних сил
- работа сторонних сил. Сторонние силы совершают положительную работу по перемещению положительного заряда, если направления сторонних сил 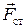 и электрического тока совпадают (рис. 3), в противном случае – работа сторонних сил отрицательна.
и электрического тока совпадают (рис. 3), в противном случае – работа сторонних сил отрицательна.
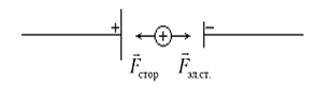 |
| Рис. 3. |
Учитывая, что общее сопротивление на неоднородном участке электрической цепи складывают из внешнего  и внутреннего
и внутреннего  сопротивлений, и приравняв выражения (6), (7) получим
сопротивлений, и приравняв выражения (6), (7) получим
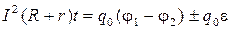 .
.
Принимая во внимание формулу (1), преобразуем выражение в вид:
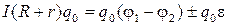 . (8)
. (8)
Сократим полученное выражение на заряд 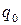 и получим закон Ома для неоднородного участка электрической цепи
и получим закон Ома для неоднородного участка электрической цепи
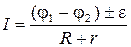 .
.
При использовании этого закона необходимо учитывать правило знаков: направление обхода участка цепи задает индексация потенциалов. ЭДС источника тока 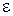 берут со знаком «плюс», если направления сторонних сил
берут со знаком «плюс», если направления сторонних сил 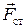 и обхода участка электрической цепи совпадают (рис. 4а), в противном случае – наоборот (рис. 4б).
и обхода участка электрической цепи совпадают (рис. 4а), в противном случае – наоборот (рис. 4б).
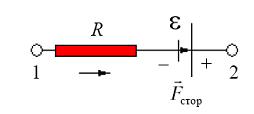 | 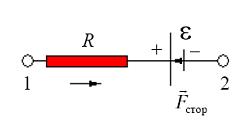 |
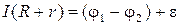 | 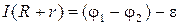 |
| а | б |
| Рис.4 |
Если цепь замкнута, т.е. 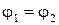 и
и 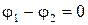 , то получим закон Ома для замкнутой электрической цепи (эл. схема на рис. 1а).
, то получим закон Ома для замкнутой электрической цепи (эл. схема на рис. 1а).
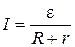
На практике ЭДС источника тока 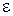 невозможно непосредственно измерить с помощью обычного вольтметра, т.к. вольтметр измеряет только разность потенциалов
невозможно непосредственно измерить с помощью обычного вольтметра, т.к. вольтметр измеряет только разность потенциалов 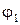 и
и 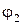 на клеммах источника. Из выражения (8) следует, что ЭДС источника тока
на клеммах источника. Из выражения (8) следует, что ЭДС источника тока 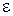 возможно найти через разность потенциалов на клеммах источника (
возможно найти через разность потенциалов на клеммах источника ( 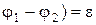 , если сила тока на участке электрической цепи равна нулю. Данное условие реализуют методом компенсации. Необходимую для компенсации разность потенциалов получают с помощью потенциометра (рис. 5). Потенциометр представляет собой навитую на изолирующую основу калиброванную проволоку, по которой может скользить контакт (такое устройство называется реохордом). Передвигая контакт C от точки A к B , можно получить любую разность потенциалов от 0 до
, если сила тока на участке электрической цепи равна нулю. Данное условие реализуют методом компенсации. Необходимую для компенсации разность потенциалов получают с помощью потенциометра (рис. 5). Потенциометр представляет собой навитую на изолирующую основу калиброванную проволоку, по которой может скользить контакт (такое устройство называется реохордом). Передвигая контакт C от точки A к B , можно получить любую разность потенциалов от 0 до 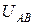 (
( 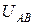 по абсолютной величине всегда меньше ЭДС вспомогательного источника).
по абсолютной величине всегда меньше ЭДС вспомогательного источника).
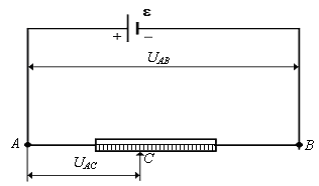
Рис. 5.
Сущность метода компенсации заключается в том, что измеряемую ЭДС неизвестного источника тока 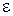 (рис. 5) компенсируют напряжением на участке потенциометра (реохорда). Компенсацию достигают, перемещая контакт потенциометра С (рис. 6) до тех пор, пока гальванометр Г не покажет нулевого значения силы тока.
(рис. 5) компенсируют напряжением на участке потенциометра (реохорда). Компенсацию достигают, перемещая контакт потенциометра С (рис. 6) до тех пор, пока гальванометр Г не покажет нулевого значения силы тока.
Рис. 6.
Обозначим величины потенциалов на концах реохорда через  и
и 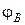 , потенциалы на концах источника тока - через
, потенциалы на концах источника тока - через 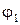 и
и 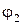 . Пусть при определенном положении контакта С на потенциометре ток не идет через гальванометр Г и источник тока с ЭДС
. Пусть при определенном положении контакта С на потенциометре ток не идет через гальванометр Г и источник тока с ЭДС 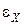 , то
, то 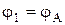 и
и 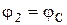 , поэтому
, поэтому
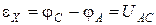 . (9)
. (9)
Согласно закону Ома
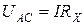 , (10)
, (10)
где 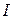 - сила тока в потенциометре,
- сила тока в потенциометре, 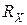 - сопротивление участка АС.
- сопротивление участка АС.
Приравняв выражения (9) и (10) получим
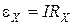 .
.
Чтобы не производить для определения неизвестного ЭДС источника тока 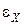 измерения силы тока
измерения силы тока 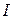 и сопротивления
и сопротивления 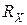 , прибегают к сравнению неизвестной ЭДС
, прибегают к сравнению неизвестной ЭДС 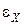 с известной
с известной 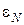 . Для этого включают вместо источника с ЭДС
. Для этого включают вместо источника с ЭДС 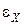 (рис. 6) источник с известной ЭДС
(рис. 6) источник с известной ЭДС 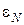 (ЭДС нормального источника тока). Вновь достигают компенсации, перемещая подвижный контакт С до нулевого показания гальванометра. Вследствие этого ЭДС источника тока определяют как
(ЭДС нормального источника тока). Вновь достигают компенсации, перемещая подвижный контакт С до нулевого показания гальванометра. Вследствие этого ЭДС источника тока определяют как
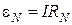 . (11)
. (11)
В условиях компенсации ток течет только по цепи, включающей потенциометр. При этом сила тока будет одинакова. Разделим равенства (10) на (11), сократив на силу тока 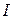 , получим условие:
, получим условие:
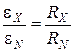 . (12)
. (12)
В виду того потенциометр изготовлен из однородного провода, электрическое сопротивление которого определяют по формуле (4), то подставим данную формулу в выражение (12) и выразим ЭДС исследуемого источника тока
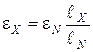 , (13)
, (13)
где 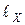 и
и 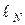 - длины участков, на которых происходит компенсация ЭДС неизвестного источника тока
- длины участков, на которых происходит компенсация ЭДС неизвестного источника тока 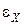 и нормального источника тока
и нормального источника тока 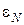 соответственно.
соответственно.
Необходимо также учитывать, что нормальные элементы быстро выходят из строя при пропускании через них больших токов, поэтому в цепь гальванометра вводят дополнительное сопротивление, ограничивающее силу тока через нормальный элемент и гальванометр.
Описание установки
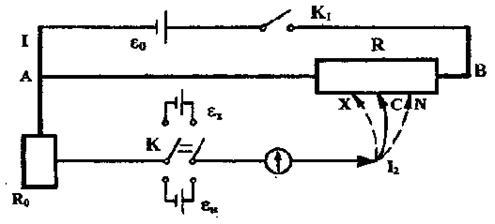 |
| Рис. 7. |
Порядок выполнения работы
1. Включить электрическую цепь с помощью ключа К1 (рис. 7). Переключатель К поставить в положение соответствующее подключению источника 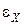 .
.
2. Передвигая свободный контакт по реохорду найти такое положение, при котором ток через гальванометр будет равен нулю (стрелка гальванометра должна показывать нуль).
3. Измерить длину участка 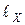 по сантиметровой линейке, на котором происходит компенсация ЭДС неизвестного источника тока. Результаты измерений занести в табл. 1. Повторить измерения 5 раз согласно п.2.
по сантиметровой линейке, на котором происходит компенсация ЭДС неизвестного источника тока. Результаты измерений занести в табл. 1. Повторить измерения 5 раз согласно п.2.
Таблица 1
| i | 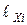 , см , см | 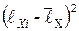 | 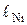 , см , см | 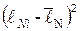 |
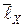 , см , см | 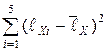 | 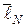 , см , см | 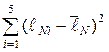 | |
4. Замкнуть ключ К на нормальный элемент  и повторить измерения по п.2, 3. Значение длины участка
и повторить измерения по п.2, 3. Значение длины участка 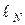 , на котором происходит компенсация ЭДС нормального элемента, занести в таблицу 1.
, на котором происходит компенсация ЭДС нормального элемента, занести в таблицу 1.
5. Рассчитать средние значения длин участков потенциометра 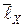 ,
, 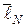 на которых происходит компенсация ЭДС неизвестного и нормального источника токов и средние квадратичные отклонения от средних значений этих величин.
на которых происходит компенсация ЭДС неизвестного и нормального источника токов и средние квадратичные отклонения от средних значений этих величин.
6. По формуле (13), подставляя в нее средние значения 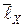 ,
, 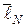 и
и 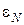 (см. на установке), определить средние значения ЭДС неизвестного источника тока.
(см. на установке), определить средние значения ЭДС неизвестного источника тока.
7. Вычислить доверительную границу общей погрешности для длин 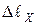 и
и 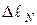 , на которых происходит компенсация ЭДС неизвестного и нормального источников тока по формулам
, на которых происходит компенсация ЭДС неизвестного и нормального источников тока по формулам
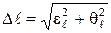 ,
,
где 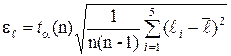 ,
, 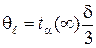 ,
, 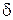 - диаметр проволоки реохорда (0,4 мм).
- диаметр проволоки реохорда (0,4 мм).
8. Рассчитать относительную ошибку измерений длин, на которых происходит компенсация ЭДС источников токов по формуле
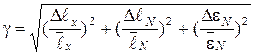 ,
,
где величина 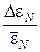 указана на установке.
указана на установке.
9. Определить абсолютную ошибку измерений для ЭДС неизвестного источника тока по формуле
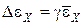
10. Записать окончательный результат измерения в виде
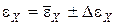 , при
, при 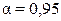 .
.
Контрольные вопросы
1.Что такое электрический ток, сила тока, плотность тока?
2. Вывести закон Ома для неоднородного участка электрической цепи и получит из него закон Ома для полной замкнутой и однородного участка электрической цепи.
3. Каков физический смысл ЭДС? Что такое сторонние силы? Каково их назначение?
4 Чем компенсируется неизвестная ЭДС при достижении нулевого показания гальванометра?
5. Если в схеме компенсации источник заменить другим источником с такой же ЭДС, но с большим внутренним сопротивлением, то в какую сторону следует сместить движок реохорда для восстановления компенсации?
ЛАБОРАТОРНАЯ РАБОТА 5
