Примеры решения основных задач
Задача 1. Определить МНК по заданной последовательности (132) на углы: 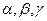 :
:
%FILE: Task _1.1
clear
clc
grd=180/pi;
% alpha=30/grd; beta=-20/grd; gamma=60/grd;
syms alpha beta gamma
C=roty(gamma)*rotz(beta)*rotx(alpha)
-------------------------
C =[ cos(gamma)*cos(beta), cos(gamma)*sin(beta)*cos(alpha)+sin(gamma)*sin(alpha), cos(gamma)*sin(beta)*sin(alpha)-sin(gamma)*cos(alpha)]
[ -sin(beta), cos(beta)*cos(alpha), cos(beta)*sin(alpha)]
[ sin(gamma)*cos(beta), sin(gamma)*sin(beta)*cos(alpha)-cos(gamma)*sin(alpha), sin(gamma)*sin(beta)*sin(alpha)+cos(gamma)*cos(alpha)]
>>
►
%FILE: Task _1.2
clear
clc
grd=180/pi;
% alpha=30/grd; beta=-20/grd; gamma=60/grd;
C=roty(gamma)*rotz(beta)*rotx(alpha)
-------------------------
C =
0.4698 0.2849 -0.8355
0.3420 0.8138 0.4698
0.8138 -0.5065 0.2849
>>
►
Задача 2. Определить кватернион, определяющий ориентацию подвижной системы координат после заданной последовательности (132) на углы: 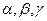 :
:
%FILE: Task _2.1
clear
clc
syms alpha beta gamma
q1=qw2(alpha);
q2=qw3(gamma);
q3=qw1(beta);
Q1=mult4quater(q1,q3);
Q=mult4quater(Q1,q2)
-------------------------
Q =
[ cos(1/2*alpha)*cos(1/2*beta)*cos(1/2*gamma)+sin(1/2*alpha)*sin(1/2*beta)*sin(1/2*gamma)]
[ cos(1/2*alpha)*sin(1/2*beta)*cos(1/2*gamma)+sin(1/2*alpha)*cos(1/2*beta)*sin(1/2*gamma)]
[ -cos(1/2*alpha)*sin(1/2*beta)*sin(1/2*gamma)+sin(1/2*alpha)*cos(1/2*beta)*cos(1/2*gamma)]
[ cos(1/2*alpha)*cos(1/2*beta)*sin(1/2*gamma)-sin(1/2*alpha)*sin(1/2*beta)*cos(1/2*gamma)]
>>
►
%FILE: Task _2.2
clear
clc
grd=180/pi;
alpha=30/grd; beta=-20/grd; gamma=60/grd;
q1=qw2(alpha);
q2=qw3(gamma);
q3=qw1(beta);
Q1=mult4quater(q1,q3);
Q=mult4quater(Q1,q2)
-------------------------
Q =
0.8013
-0.0178
0.3046
0.5145
>>
►
Задача 3. Определить проекции угловой скорости подвижной системы координат на ее оси по заданной матриче направляющих косинусов ( см. задачу 1):
%FILE: Task _3
clear
clc
syms alpha beta gamma dalpha dbeta dgamma wx wy wz
Cms=roty(gamma)*rotz(beta)*rotx(alpha);
dCms=diff(Cms,alpha)*dalpha+diff(Cms,beta)*dbeta+diff(Cms,gamma)*dgamma;
Wms_m=Cms*dCms.';
w1=simple(Wms_m(3,2))
w2=simple(Wms_m(1,3))
w3=simple(Wms_m(2,1))
>>
-------------------------
w1 = cos(gamma)*dalpha*cos(beta)-sin(gamma)*dbeta
w2 = dgamma-dalpha*sin(beta)
w3 = dbeta*cos(gamma)+cos(beta)*dalpha*sin(gamma)
>>
►
Задача 4. Получить кинематические уравнения (по данным задачи 3):
%FILE: Task_4
clear
clc
syms alpha beta gamma wx wy wz
A=[cos(gamma)*cos(beta),-sin(gamma),0
-sin(beta),0,1
cos(beta)*sin(gamma),cos(gamma),0];
B=[wx;wy;wz];
X=simple(inv(A)*B);
dalpha=X(1)
dbeta=X(2)
dgamma=X(3)
-------------------------
dalpha = (cos(gamma)*wx+sin(gamma)*wz)/cos(beta);
dbeta = -sin(gamma)*wx+cos(gamma)*wz;
dgamma = (cos(gamma)*sin(beta)*wx+wy*cos(beta)+sin(gamma)*sin(beta)*wz)/cos(beta).
>>
►
Задача 5. Построить матрицу (с ортогональными параметрами) определяющую положение системы координат после поворота и затем – перемещения;
%FILE: Task _5.1
clear
clc
syms alpha beta gamma x y z
Cms=roty(gamma)*rotz(beta)*rotx(alpha);
T=rotort(Cms.');
R=[x;y;z];
P=moveort(R);
W=simple(T*P)
-------------------------
W =
[ cos(gamma)*cos(beta), -sin(beta), sin(gamma)*cos(beta), cos(gamma)*cos(beta)*x-sin(beta)*y+sin(gamma)*cos(beta)*z]
[ cos(gamma)*sin(beta)*cos(alpha)+sin(gamma)*sin(alpha), cos(beta)*cos(alpha), sin(gamma)*sin(beta)*cos(alpha)-cos(gamma)*sin(alpha), (cos(gamma)*sin(beta)*cos(alpha)+sin(gamma)*sin(alpha))*x+cos(beta)*cos(alpha)*y+(sin(gamma)*sin(beta)*cos(alpha)-cos(gamma)*sin(alpha))*z]
[ сos(gamma)*sin(beta)*sin(alpha)-sin(gamma)*cos(alpha), cos(beta)*sin(alpha), sin(gamma)*sin(beta)*sin(alpha)+cos(gamma)*cos(alpha), (cos(gamma)*sin(beta)*sin(alpha)-sin(gamma)*cos(alpha))*x+cos(beta)*sin(alpha)*y+(sin(gamma)*sin(beta)*sin(alpha)+cos(gamma)*cos(alpha))*z]
[ 0, 0, 0, 1]
>>
►
% FILE: Task _5.2
clear
clc
grd=180/pi;
alpha=30/grd; beta=-20/grd; gamma=60/grd;
R=[1;2;3];
Cms=roty(gamma)*rotz(beta)*rotx(alpha);
T=rotort(Cms.');
% R=[x;y;z];
P=moveort(R);
W=(T*P)
-------------------------
W =
0.4698 0.3420 0.8138 3.5953
0.2849 0.8138 -0.5065 0.3930
-0.8355 0.4698 0.2849 0.9589
0 0 0 1.0000
>>
►
Задача 6. Построить матрицу (с ортогональными параметрами) определяющую положение географической системы координат:
%FILE: Task _6.
clear
clc
syms u lambda phi Rg h
Cms=rotz(phi)*rotx(lambda)*rotx(u);
T=rotort(Cms.');
R=[0;Rg+h;0];
% R=[x;y;z];
P=moveort(R);
W=(T*P)
-------------------------
W =
[ cos(phi), -sin(phi), 0, -sin(phi)*(Rg+h)]
[ sin(phi)*(-sin(lambda)*sin(u)+cos(lambda)*cos(u)), cos(phi)*(-sin(lambda)*sin(u)+cos(lambda)*cos(u)), -sin(lambda)*cos(u)-cos(lambda)*sin(u), cos(phi)*(-sin(lambda)*sin(u)+cos(lambda)*cos(u))*(Rg+h)]
[ sin(phi)*(sin(lambda)*cos(u)+cos(lambda)*sin(u)), cos(phi)*(sin(lambda)*cos(u)+cos(lambda)*sin(u)), -sin(lambda)*sin(u)+cos(lambda)*cos(u), cos(phi)*(sin(lambda)*cos(u)+cos(lambda)*sin(u))*(Rg+h)]
[ 0, 0, 0, 1]
>>
►
Задача 7.Найти проекции вектора перемещения географической системы координат на оси инерциальной системы координат:
(в продолжение решения задачи 6)
s=simple(Cms*W(1:3,4))
-------------------------
s =
[ 0]
[ Rg+h]
[ 0]
>>
►
Задача 8. Определить проекции линейной скорости географической системы координат на ее оси
%FILE: Task _8
clear
clc
grd=180/pi;
% alpha=30/grd; beta=-20/grd; gamma=60/grd;
syms u lambda phi Rg h Omega dlambda dphi dh
Cms=rotz(phi)*rotx(lambda)*rotx(u);
T=rotort(Cms.');
R=[0;Rg+h;0];
P=moveort(R);
W=simple(T*P);
% s=simple(Cms*W(1:3,4))
dW=diff(W,u)*Omega+diff(W,lambda)*dlambda+diff(W,phi)*dphi+diff(W,h)*dh;
Vo=simple(dW(1:3,4));
Vg=Cms*Vo;
vx=simple(Vg(1))
vy=simple(Vg(2))
vz=simple(Vg(3))
--------------------------
vx = -dphi*Rg-dphi*h
vy = dh
vz = Omega*cos(phi)*h+dlambda*cos(phi)*Rg+Omega*cos(phi)*Rg+dlambda*cos(phi)*h
>>
►
Залача 9.Вычисление матрицы направляющих косинусов по заданному кватерниону:
%FILE_ Task _9.1
clear
clc
syms p0 p1 p2 p3 e0 e1 e2 e3
p=[p0;p1;p2;p3];
C=mdc2quater(p)
----------------------
C =
[ (p0^2+p1^2-p2^2-p3^2)/(p0^2+p1^2+p2^2+p3^2)^2, (2*p1*p2+2*p0*p3)/(p0^2+p1^2+p2^2+p3^2)^2, (2*p1*p3-2*p0*p2)/(p0^2+p1^2+p2^2+p3^2)^2]
[ (2*p1*p2-2*p0*p3)/(p0^2+p1^2+p2^2+p3^2)^2, (p0^2-p1^2+p2^2-p3^2)/(p0^2+p1^2+p2^2+p3^2)^2, (2*p2*p3+2*p0*p1)/(p0^2+p1^2+p2^2+p3^2)^2]
[ (2*p1*p3+2*p0*p2)/(p0^2+p1^2+p2^2+p3^2)^2, (2*p2*p3-2*p0*p1)/(p0^2+p1^2+p2^2+p3^2)^2, (p0^2-p1^2-p2^2+p3^2)/(p0^2+p1^2+p2^2+p3^2)^2]
>>
-------------------------
%FILE_Task_9.2
clear
clc
p=[10; -20; 23; 41]
C=mdc2quater(p)
U=C.'*C
-------------------------
p =
-20
C =
-0.6310 -0.0369 -0.7749
-0.6421 -0.5358 0.5483
-0.4354 0.8435 0.3144
U =
1.0000 0 0
0 1.0000 0.0000
0 0.0000 1.0000
>>
►
