Чмтмь главного масштаба карты

I ?' На построенной сетке, как и в цилиндрической квадратной проек-

I ЛйИ| показатели п, р, k численно равны. «Сжатие» поверхности гло-

fM Hi участке между параллелями сечения при его изображении

ЦИЛИНДре, а затем и на плоскости приводит к тому, что в этой части

I показатели искажений меньше 1. На внешних участках сетки

*ПЬше 1. На мировой карте, построенной в этой проекции, иска-

I целом меньше, чем в квадратной проекции. Например, при

■Лалях сечения 30° на широтах 45°, 60° и 75° они соответственно

HU 1,22; 1,72 и 3,34. На экваторе эти показатели равны 0,87.

ЩШЩИ1шШШМТташ11шшт

Проекция была предложена древнегреческим философом Анакси-мандром (VII—VI вв. до н. э.). В настоящее время ее применяют иногда для построения мировых карт.

Цилиндрическая нормальная равноугольная проекция Меркатора на касательном цилиндре. Вее основе лежит условие равноуголь ности, когда в любой точке показатели тип равны (рис. 158). Для достижения этого условия при построении картографической сетки промежутки между параллелями с удалением от экватора искус ственно раздвигают. Представим себе, что параллели с глобуса переносят при проектировании на касательный цилиндр. При этом каждая из них растягивается пропорционально секансу широты параллели. В такой же мере растет показатель искажения длин по параллелям п. Чтобы в каждой точке карты показатель искажения длин по меридиану был ему равен, нужно и дуги меридианов также растягивать на каждом участке пропорционально секансу широты.

Полученная сетка обладает следующими свойствами. В ней нет искажений углов, форм малых фигур. Линия нулевых искажений всех других видов — экватор. С удалением от него искажения'возраста ют. Так, на широтах 45°, 60° и 75° показатели искажения длин

160 140 120 100 80 60 40 20 0 20 40 60 80 100 120 140 160

160 140 120 100 80604020020406080 100 120 140 160

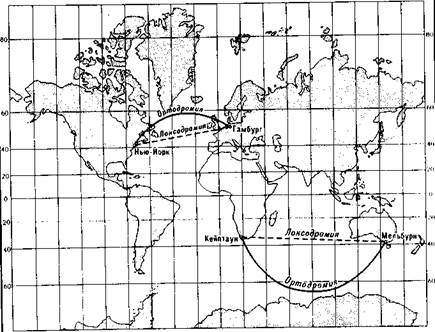
Рис. 158. Картографическая сетка в цилиндрической равноугольной проекци Меркатора с изображением ортодромий и локсодромий в северном и южном пол' шариях

гп = п соответственно равны 1,4; 2,0 и 3,85 (как и в цилиндри­ческой квадратной проекции). Показатели искажения площадей на этих же широтах составляют квадраты приведенных чисел, т. е. равны (с округлением) 2,4 и 15.

Эту неперспективную проекцию разработал в 1569 г. фламан­дец Герард Кремер, известный под фамилией Меркатор. В проекции Меркатора на удаленных от экватора территориях сильно искажают­ся длины и площади. Несмотря на это, длительное время проекция Меркатора применялась для построения мировых карт. Особенно широко проекция используется для создания морских карт с самым разным охватом территории — от мировых карт до карт отдельных заливов и портовых акваторий. Это связано с замечательным свойст­вом картографической сетки, построенной в проекции Меркатора, изображать прямой линией локсодромию любого направления.

Локсодромией называют линию на поверхности земного эллипсо­ида с постоянным румбом, т. е. образующую на всех участках один и тот же угол с пересекаемыми меридианами. Пользуясь картой, составленной в проекции Меркатора, штурману корабля очень легко установить направление его пути по локсодромии. Для этого до­статочно по линейке прочертить прямую линию между портами отправления и прибытия. Напомним, что кратчайшее расстояние на поверхности земного шара направлено по ортодромии (§ 29). Но движение по ортодромии связано с необходимостью постоянно менять курс корабля, поэтому рассчитанный по ортодромии путь делят на участки, на каждом из которых корабль направляют по локсодромии (рис. 158).

Мировые карты в проекции Меркатора можно встретить в учеб­ных атласах, изданных в России до 1917 г.

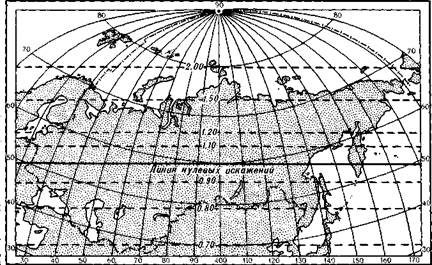
Цилиндрическая нормальная произвольная проекция Н. А. Ур-маева.Советский геодезист Н. А. Урмаев в 1949 г. разработал цилин­дрическую нормальную проекцию, у которой промежутки по меридиа­нам между параллелями, увеличиваясь от экватора, растягиваются не так сильно, как в проекции Меркатора (рис. 159). Этим достигают­ся меньшие искажения площадей, конечно, за счет потери свойства равноугольности. Об этом можно судить по величине показателей искажения площадей, которые на параллелях 45°, 60° и 75° соот­ветственно равны 1,6; 2,8 и 6,5. По сумме свойств проекция яв­ляется произвольной. В ней построены карты часовых поясов в Географическом атласе для учителей средней школы и в Учебном атласе мира.

Цилиндрическая косая произвольная проекция М. Д. Соловьева.Картографическая сетка в этой проекции строится путем вычисле­ний на косом секущем цилиндре, одна из линий сечения которого С поверхностью глобуса (шара) по малому кругу касается паралле­ли 60° с.ш. в точке ее пересечения с меридианом 100° в.д. (принимае­мым за средний меридиан карты). Ось цилиндра составляет с осьюглобуса угол в 15° (рис. 160).

На развернутом цилиндре малый круг сечения глобуса изобра­жается прямой линией, не совпадающей с параллелью. Меридианы

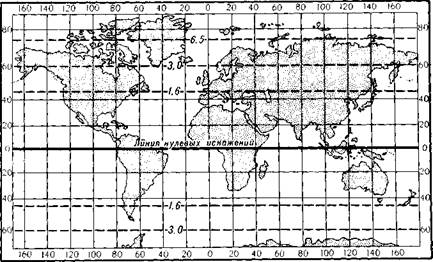Рис. 159. Картографическая сетка в цилиндрической нормальной произвольной проекции Урмаева

Рис. 161.Картографическая сетка в проекции Соловьева сизоколами площадей

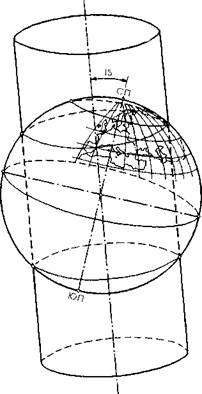Рис. 160. Положение косого секуще­го цилиндра для получения карто­графической сетки в проекции Со­ловьева

и параллели в этой проек­ции — кривые линии; проме­жутки по среднему (прямо­му) меридиану несколько увеличиваются к северу от линии малого круга сечения и уменьшаются к югу от нее. Северный полюс изобража­ется точкой.

На линии малого круга (перпендикулярной к средне­му меридиану) искажений нет (рис. 161). К северу от этой линии частные масшта­бы площади больше главно­го; показатель искажения Р в районе архипелага Север­ная Земля доходит до 2,0. К югу от линии нулевых ис­кажений показатель Р мень­ше 1, у южных границ СССР равен 0,7.

Проекция была разработана в 1937 г. для карт СССР. До не­давнего времени ее применяли для карт СССР, предназначенных для работы с учениками начальных классов. Сравнительно с дру­гими проекциями для карт СССР она обладает заметными искаже­ниями, но отличается многими методическими достоинствами. Форма сетки и особая компоновка карты в проекции Соловьева создают впе­чатление сферичности поверхности СССР и окружающих частей по­верхности Земли. Кроме того, на ней изображается весь советский сектор Арктики, вплоть до точки Северного полюса. Это позволя­ет по карте определить, какие территории в СССР расположены севернее, какие южнее. В 80-х годах проекция была заменена на более современную.

Цилиндрические поперечные проекции используются преимуще­ственно для построения крупномасштабных карт. Например, для со­ветских топографических карт применяют поперечно-цилиндриче­скую равновеликую проекцию Гаусса-Крюгера, описанную в § 8 учеб­ного пособия.

36. КОНИЧЕСКИЕ ПРОЕКЦИИ

Коническая нормальная равнопромежуточная проекция Птоле­мея.Строится на нормальном касательном конусе. Условием построе­ния картографической сетки является сохранение величины главного Масштаба по всем меридианам. Сетка может быть создана простым геометрическим построением (хотя она относится к неперспектив-

^ттттяштянтшшявШШШШШШН^'

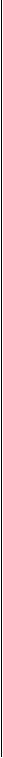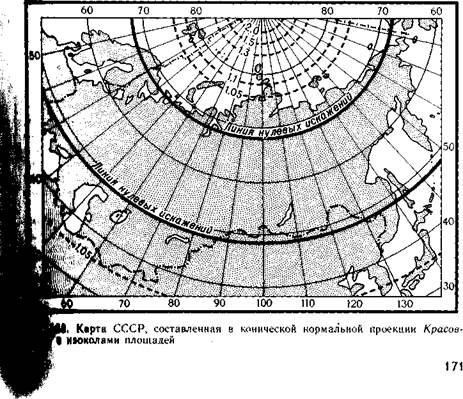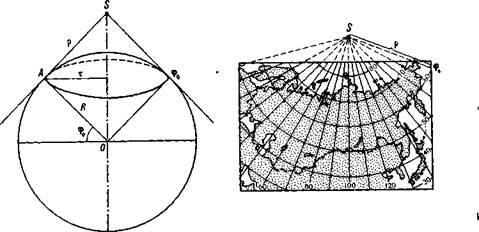
Рис. 162. Построение и внешний вид нормальной конической равнопромежуточной проекции Птолемея

ным). Рассмотрим здесь аналитический расчет элементов сетки с помощью рисунка 162.

Все параллели у этой сетки — дуги концентрических окружнос­тей с центром в точке S (вершине конуса). Формулу радиуса параллели касания конуса (с широтой ф₀) выводят из прямо­угольного треугольника AOS, в котором р и R — катеты, а угол ASO равен ф₀, как образованный взаимно перпендикулярными сто­ронами p = y?-ctg<po.

Величину промежутков между параллелями узнают по формуле:

_ 2л/?-Аур 360° '

Обе вычисленные величины (р и а) при построении сетки уменьшают в соответствии с выбранным главным масштабом. Как у каждой нормальной конической проекции, меридианы здесь имеют форму прямых линий, сходящихся в точке S под равными углами у. Угол у или сближение меридианов пропорционален разности долгот сосед­них меридианов и широте параллели касания конуса y==Ak-smy₀.

Построение сетки объясняет ее свойства: главный масштаб сохраняется по всем меридианам и по параллели касания конуса; частные масштабы по другим параллелям больше главного; пока­затели п, р и k численно равны между собой. Проекция произволь­ная, равнопромежуточная.

Она была впервые применена (или изобретена?) древнегречес­ким ученым К. Птолемеем во II в н.э. Искажения в ней невелики в полосе карты, ограниченной параллелями, отстоящими на 15^е к северу и югу от параллели касания конуса. Поэтому она пригодна для стран, вытянутых с запада на восток. Простота построения сетки позволяет рекомендовать ее для создания рукописных карт

участков территории СССР (союзных республик, областей и дру­
гих) . За параллель касания конуса выбирают при этом параллель,
{проходящую через геометрический центр изображаемой территории,
\ Коническая нормальная проекция Красовского.Картографичес­
кая сетка в проекции Красовского построена как бы на секущем
конусе. При ее расчете учитывалось требование, чтобы на большей
Части изображенной в ней территории СССР, а именно между па­
раллелями 40° и 73° с.ш., искажения площадей практически бы
отсутствовали, а на крайних параллелях этого широтного пояса
масштабы длин были бы равны. Сетка имеет форму, свойственную
нормальным коническим проекциям. _

Линии нулевых искажений длин в этой проекции расположены вдольпараллелей с широтами 50° и 68° (с округлением). Их и можнопринять за параллели сечения конуса и глобуса (шара). Промежутки по меридианам у нее равны и масштабы вдоль них близ­ки к главному (пг = 0,997). Следствием этого является близость величинпоказателей искажения длин по параллелям, площадей и форм.Абсолютные значения этих показателей малы, поэтому на большейчасти территории СССР проекция близка к равновеликим. Дажев периферийных, крайних южных и северных частях карты СССРискажения крайне малы. Так, на параллели у южной границы СССР(с одной стороны), а также на широте северных частей ■рхипелаговСеверная Земля, Новосибирских островов, северной

.1₁..11,.1.₁...1.!_П!шл1

|111

Ц|М1||1||111!Ш11||1!|!1|Ч111ц|!|Ц(Н)Р1!|Ш|1|!Ш|(111|.1!!.|..|!'! 'i'tj i „Цт^чшшфпш,., , ..u,h „(„ 10° 20" 30° 40* 50° 60° 70° 80° 90° 100° 110° 120° 130° 140° 150° 160° 170° 180° ------ ;------- »~дХ. I Рис. 164. Номограмма поправочных коэффициентов для вычисления расстояний на карте СССР, составленной в конической нормальной проекции Красовского. 9 — широта, дХ — разность долгот части полуострова Таймыр (с другой стороны) показатель искажения площадей отличается от единицы всего на 0,05 (т. е. равен 1,05). Лишь севернее перечисленных островов и полуострова он еще больше возрастает (рис. 163). Так же более заметными к периферии оказываются искажения углов. При приближении к параллели с широтой 80° с.ш. показа­тель искажения углов со достигает величины 10°. Хотя искажения на карте СССР* построенной в проекции Кра­совского, относительно невелики, их можно учесть при необходи­мости более точного определения расстояний между изображенными на ней пунктами. Выполняя такой расчет, измеренную по карте пря­мую линию между двумя пунктами (и вычисленную в главном масштабе) умножают на поправочный коэффициент Ко, найденный по номограмме (рис. 164). При этом если оба пункта располагаются на одной параллели, то значение коэффициента находят на номо­грамме по их широте (ф) и разности долгот (X). Если же пункты имеют разные широты, то поправочный коэффициент находят по средней их широте и разности долгот. Проекция была разработана советским астрономом-геодезистом Ф. Н. Красовским в 1921 г. В ней построены физическая карта СССР в атласе для 6-го класса, контурные карты СССР для этого же класса, некоторые другие учебные и справочные карты СССР. /'"^ Коническая нормальная равнопромежуточная проекция Кав-райского.Построена на секущем конусе 1с параллелями сечения 47° и 62° с.ш. На построенной в этой проекции карте СССР глав­ный масштаб длин сохраняется на параллелях сечения и на всех меридианах. В пределах материковой части СССР искажения не-     50 60 70 80 80 70 60   40 30     40 30   щ щШшщтШшшшЩтштштШш       ■:\< Х-:'";:^::--':$;^^^         60 70 80 90 100 ПО 120 130 140           Рис.165. Карта СССР, составленная в конической нормальной равнопромежуточной проекции Каврайского, с изоколами площадей             0,90-           0.85^^: Ъ84. 5?5 ■ад?: ■°.вв.                           0,99       0,98. ^°.9е   °-*.^%\ N           '•00.^                   s                                         ■1.00         '■°os ^             \                                 S   0.97   ■%. Ч     °э9.             \ \ \ 0,70 0.7-4 0.76 80° 75° 70° 65° 60" 85" 80" 45" 40" as----------------- „ Ю" 20" 30° 40° 50° 60 70 80° 90° 100 ПО 120 130 140 150 160 170 180 -------------------- »-ДХ , 166.Номограмма поправочных коэффициентов для вычисления расстояний на • СССР,составленной в конической нормальной равнопромежуточной проекции райского. <|i широта, ДХ— разность долгот                         значительны. Между параллелями сечения на широте 55° п, р и k равны 0,99, а во внешнюю сторону от параллелей сечения эти показатели больше единицы (рис. 165). По величине искажения углов проекция близка к проекции Красовского. При необходимости измерения точных расстояний между пункта- \ ми по карте СССР, составленной в проекции Каврайского, следует / использовать поправочный коэффициент /Со, взятый с номограммы (рис. 166). Прием определения величины коэффициента аналогичен тому, что описан при характеристике проекции Красовского. Проекция была разработана советским картографом, геодезистом и астрономом В. В. Каврайским в 1931 г. и с тех пор нашла широкое применение для карт СССР — в географических атласах для сред­ней школы (кроме карт для 3 и 4-го классов), в Географическом атласе для учителей средней школы. § 37. ПОЛИКОНИЧЕСКИЕ ПРОЕКЦИИ. ПСЕВДОЦИЛИНДРИЧЕСКИЕ ПРОЕКЦИИ Поликоническая произвольная проекция ЦНИИГАиК (ва^и} ант 1950г.). Рассматриваемая поликоническая проекция (как и вс£ другие поликонические) отличается тем, что экватор и средний мери­ диан — взаимно перпендикулярные прямые; остальные меридианы 4- кривые, а параллели — дуги эксцентрических окружностей. Средний меридиан разделен параллелями на равные части; все параллели также равноразделены. —J Главный масштаб длин сохраняется вдоль среднего меридиана и по параллелям с широтами 48°. Между этими параллелями он меньше главного (на экваторе п = 0,82). Во внешнюю сторону от параллелей 48° показатель п>\. Своеобразно распределение иска­жений площадей: линия нулевых искажений площадей имеет форму неправильной замкнутой фигуры (рис. 167). Внутри этой линии р<1 ив центре мировой карты достигает минимальной величи­ны 0,82. Во внешнюю сторону от ЛНИ показатель р больше, доходя вблизи северной рамки мировой карты до 2,0. ГЪ.этой проекции углы искажаются] что хорошо видно по фор­ме картографической сетки; в угловых частях показатель со пре­вышает 50°. Проекция была разработана в Центральном научно-исследова­тельском институте геодезии, аэрофотосъемки и картографии (ЦНИИГАиК) картографом Г. А. Гинзбургом. Поликоническая произвольная проекция ЦНИИГАиК (вариант БСЭ).В отличие от предыдущей в данной поликонической проекции промежутки вдоль среднего меридиана с удалением от экватора воз- ; растают, а параллели имеют несколько большую кривизну. В целом \ же сетка похожа на картографическую сетку в варианте проекции \ 1950 г. (рис. 168). Главный масштаб длин сохраняется в ней на параллелях с широ­той 45° и в точке пересечения среднего меридиана с экватором.   ^, 168.Мировая карта в поликонической произвольной проекции ЦНИИГАиК рнантБСЭ) с изоколами площадей Рис.167. Мировая карта в поликонической произвольной проекции ЦНИИГАиК (вариант 1950 г.) с изоколами площадей       160 160 120 80 40 0 40 80 120 160 160 120     60 90 40 30 20 10 0 10 30 30 40 ВО 1 И     МейЖл vvv^ V^b* 60 50 40     Т^Ш^Щ^^ГГГТ^1' ШР                         \1шш*,ъ ."■.".■!   #$# ЙШэ i*v5       те^ЧЬ^вьЙг/'/ /                           '■:'•*       v^                     »■ "* •"*           1L- J   ¥ *s3^U       \4 '       4 /     f>jf               i       fW           1 VI 1       •■'■:fx':               0.83               / 1     Л \*\   VJ^!:s№h •-0 Э-,         E-     1 LH     ФуУУ^ /.'/ /         L Г   :;frjy w .- "             \^t^j^JftH®5t*W^^ Hvjieehix шнашении^л         XXVVwwA rVxl     . IJ -/-A / У*7                         vVvS^rv^^W           sLU/j^/yC       ^S^S^2^^rr\   Ш       160 120 80 40 0 40 80 120 160 160                                                       С удалением от экватора по среднему меридиану масштаб длин воз­растает. В сторону экватора от параллелей с широтой 45° масштабы длин меньше главного (на экваторе п = 0,83), а во внешнюю сто­рону от этих параллелей он больше главного. Линия нулевых искажений площадей имеет форму эллипса, вьь тянутого с запада на восток и касающегося на севере и на юге па| раллели с широтами 45°. Внутри эллипса р<\ (в центре р = 0,83)! а во внешнюю сторону от линии нулевых искажений р>\. Вблизи северной и южной рамок мировой карты этот показатель приобретаем значение 2—3. Искажение углов имеет несколько иное распределение по площади карты, но абсолютное максимальное значение пока^ затель искажения углов имеет примерно такую же величину, как и в проекции 1950 г. Проекция была разработана Г. А. Гинзбургом в то же время, как и в варианте 1950 г. для мировых карт в Большой советской энцик­лопедии (отсюда и название варианта). Псевдоцилиндрическая равновеликая проекция Сансона. Экватор и средний меридиан в проекции Сансона — взаимно перпендикуляр­ные прямые линии, равноразделенные и построенные в главном мас­штабе (рис. 169). Параллели — прямые, параллельные экватору, также равноразделенные меридианами и также сохраняющие глав­ный масштаб длин. Все меридианы (кроме среднего) — кривые линии с масштабами длин больше главного. Картографическая сетка обла­дает свойством равновеликости и как таковая сильно искажает уг­лы, что видно по внешнему виду сетки. Рис. 169. Картографическая сетка в псевдоцилиндрической равновеликой проекции Сансона для мировой карты Картографическую сетку в проекции Сансона можно построить весьма просто. Для этого нужно прямо с глобуса взять размеры отрезков экватора, среднего меридиана и параллелей и в перечис­ленной последовательности нанести их на бумагу. Кривые линии леридианов при этом чертят через точки деления параллелей на глаз или по лекалу. ] Можно для построения сетки размеры отрезков экватора, ме­ридиана (среднего) и параллелей взять из таблицы длин дуг па­раллелей и меридианов, помещенной в Географическом атласе для учителей средней школы. Проекция Сансона была предложена фран­цузским географом в XVII в. Она удобна для школьных карт южных материков — Африки, Южной Америки и Австралии, а также для карт областей СССР, вытянутых с севера на юг. 7 Псевдоцилиндрическая произвольная проекция Урмаева. Близ­ка по виду сетки и свойствам к проекции Сансона, но проме­жутки по среднему меридиану между параллелями у нее с удале-|« нйем от экватора незначительно уменьшаются. Масштабы длин по параллелям не остаются в ней неизменными, но увеличиваются с широтой. Имея искажения всех видов, проекция близка к равнове­ликим. Разработана проекция Н. А. Урмаевым. Она использована, в част­ности, для карты Тихого океана в Географическом атласе для учителей средней школы. § 38. УСЛОВНЫЕ ПРОЕКЦИИ Условная проекция ЦНИИГАиК с несимметричной сеткой для карт СССР. Условиями для расчета этой проекции были следующие: а) параллели должны быть кривыми линиями, по кривизне примерно равными параллелям в цилиндрической косой проекции Соловьева; б) Северный полюс/должен изображаться точкой, картографическая се-пка должна обДдать свойством глобулярности (как проекция Соловьева); в) изображение европейской части СССР на карте должно быть несколько увеличено (построено в более крупном мас­ штабе) по сравнению с азиатской частью из-за меньшей загру­ женности последней. В результате выполненных расчетов получилась картографичес­кая сетка, в общем похожая на сетку проекции Соловьева, не­симметричная относительно среднего прямого меридиана с долго­той 100° в. д. В ее восточной части меридианы сближены (рис. 170). Кроме среднего меридиана, все линии сетки — кривые линии. Сетка имеет искажения всех видов. Изоколы искаженияплоща-дейимеют сложную конфигурацию, линия нулевых искажений площа­дей сечет косо европейскую часть СССР, направляясь в целом с Юго-запада на северо-восток, а в азиатской части она следует ■близипобережья Северного Ледовитого океана. К северу от нее Наблюдается небольшое увеличение масштабов площадей, к югу — ИХ уменьшение (см. рис. 170). Проекция заметно искажает углы, осо-MHHOвблизи северных и восточных окраин карты СССР. L■ Проекция была разработана в ЦНИИГАиК Г. А. Гинзбургом и "|. М. Богинским. Предназначалась она для построения карт СССР ITViacax для начальных классов средней школы. В этом назначе- 72 Каота полушария в глобулярной проекции Арроусмита с изоколами площа-:,шаваР"построение линий картографической сетки в проекции Арроусмита   Рис. 170. Карта СССР в условной произвольной проекции ЦНИИГАиК с несим­метричной сеткой, с изоколами площадей   60 70 80 80 70 60 5С   10 0 10 2С \ ^^С^*^^^\У/s7/y Vet* * эГ ' *** *^Ча-У Ж1' '*"• Л» jft" f' ' T   fit 1 * Тй ^ \ \ /* 30 20 10 0 10 20       1 \           \         &Л- i„,i (J •         2f££ tucHttmt                 _ 30 40 50 60 70 80 90 100 110 120 130   Рис. 171. Карта Евразии в условной проекции ЦНИИГАиК (вариант 1) с изо­колами площадей нииона должна была заменить цилиндрическую косую проекцию Толовьева, у которой слишком велики искажения площадей в аркти- Н^оРванЙа0яНпроекция ЦНИИГАиК для карт Евразии (вариант 1). ■Автографическаясетка в этой проекции должна была удовлетворять Тдующим условиям: а) параллели по форме должны быть пологи- мДивымилиниями; б) масштаб площади в пределах Европы дол- жёнбыть крупнее, чем в азиатской части материка, но в целом иска- , жйнияплощадей должны быть небольшими. . ~ На полученной сетке, удовлетворяющей этим условиям, парал­лели и меридианы - кривые линии. Сетка несимметрична относитель­но среднего меридиана: расстояния между соседними меридианами || западной части карты больше, чем в восточной. Искажения пло­щадей в пределах материковой части Евразии невелики, только в Самой северо-западнойчасти несколько превышают одну десятую ■долюглавного масштаба (рис. 171). Искажения углов имеются, Кблизи северных окраин материка они заметны даже на глаз. F Проекция была разработана в 1969 г. Л. С. Дедовской и с тех Ьорона применяется для карт Евразии в атласе для 7 класса, для Цучебных стенных карт Евразии. йс. 1 •Й. Спр V Условная глобулярная (шаровая) произвольная проекция fADDOvcMHTa.В этой проекции строят изображения западного и вос-Г точногополушарий Земли. Экватор в ней представлен прямой ли- нией, равной половине земного экватора в главном масштабе кар­ты; средний меридиан — прямая, равная по длине экватору и ему перпендикулярная. Внешний меридиан карты представляет собой окружность с центром в точке пересечения экватора со средним меридианом. Для построения остальных меридианов и параллелей экватор, средний и крайний меридианы делят на равные части, количество которых зависит от принимаемой густоты сетки. Затем проводят эти недостающие линии картографической сетки в виде дуг окружностей, каждую через соответствующие три точки (рис. 172). Для параллели это две точки на крайнем и одна на среднем меридианах. Для нахождения центра данной параллели соединя­ют прямой линией две точки пересечения с внешним и средним меридианом. Эту линия делят пополам и из середины восстанавли­вают перпендикуляр до пересечения с продолжением линии сред­него меридиана. Точка пересечения и явится центром дуги па­раллели. Для проведения меридианов опорными точками являются полюса и одна точка на экваторе. Для нахождения центра дуги меридиана точку полюса соединяют прямой с точкой этого меридиана на эква­торе; из ее середины проводят перпендикуляр до пересечения с линией экватора или ее продолжения. Из построения сетки видно, что главный масштаб длин сохра­няется у нее по экватору и среднему меридиану. На остальных ме­ридианах и параллелях частные масштабы длин больше главного — на крайнем меридиане показатель искажения длин т= 1,57. В такой же степени от центра карты к ее краю возрастает показатель иска­жения площадей (1<р<1,57). Сетка имеет небольшие искажения углов. По внешнему виду и свойствам картографическая сетка в данной проекции близка к азимутальной поперечной проекции По-стеля. Разработал ее английский картограф Арроусмит (1750—1828), который и назвал ее шаровой, или глобулярной. Простота построе­ния сетки позволяет рекомендовать ее для изготовления рукопис­ных карт полушарий силами школьников. § 39. ОПРЕДЕЛЕНИЕ (РАСПОЗНАВАНИЕ) ПРОЕКЦИЙ. ПРИНЦИПЫ ВЫБОРА КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ. КОМПОНОВКА КАРТ Определение проекций.В предыдущих параграфах охарактеризо­вано двадцать видов картографических проекций. Вообще же в картографии применяется еще большее их количество. Все они раз­личаются внешним видом картографической сетки и свойствами кар­тографического изображения. Но при использовании географических карт требуется знание их математических свойств, в частности сте­пени искаженности изображения и распределения искажений по площади карты, а это целиком зависит от проекции, в которой карта построена. С первого взгляда на картографическую сетку можно отличить класс проекции (цилиндрическая, коническая или иная). Но для распознавания конкретного вида проекции необходимо выполнить измерения элементов картографической сетки. Известно, что наибольшие искажения наблюдаются на картах с большим охватом территории — мировых и изображающих полуша­рия Земли. Распознавание примененных для их построения проекций (охарактеризованных в § 35, 37) можно выполнить с помощью определителей (таблицы 10, 11). В определителе проекций миро­вых карт две ступени определения: сначала по форме меридианов и параллелей устанавливают класс проекций, а затем по измене­нию величины промежутков между параллелями по среднему мериди­ану карты с удалением от экватора — конкретный вид проекции. Названия последних помещены в таблицах в сокращенной форме. Карты полушарий строят преимущественно в азимутальных проекциях, поэтому при их определении (табл. 11) первая ступень распознавания сразу же указывает вариативные виды возможных конкретных проекций. Вторая ступень определения позволяет уточ­нить тот вид проекции, в котором построена анализируемая карта. Для карт северного (южного) полушарий употребляют неболь­шое число азимутальных нормальных проекций, чаще других — Таблица 10