Показания акселерометров
Для определения показаний акселерометров сначала найдем соответствующие производные от матрицы-вектора 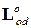 (см. формулу (1.5)), т.е.
(см. формулу (1.5)), т.е. 
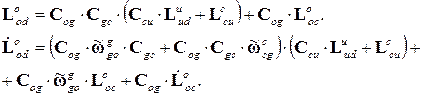
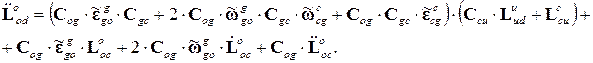
Затем найдем эти матрицы-вектора в проекциях на оси системы координат датчиков
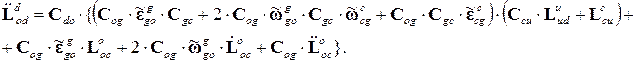

Здесь
 (1.14)
(1.14)
Следовательно показания акселерометров с учетом ускорения земного притяжения 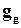 примут вид:
примут вид:
 ; (1.15)
; (1.15)
где 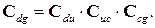
4.5. Контрольные вопросы
1. Дать определение однородным координатам.
2. Запишите и прокомментируйте формулы для элементарных преобразований: вращения (поворота) и переноса.
3. Как определяются с помощью однородной матрицы перемещения параметры вектора в системе координат s, заданного в системе координат m?
4. Как определяется с помощью аппарата однородных параметров вектор абсолютного линейного ускорения системы координат "m", выраженный в проекциях на оси этой системы координат?
5. Как определяется с помощью аппарата однородных параметров вектор абсолютной угловой скорости системы координат "m", выраженный в проекциях на оси этой системы координат?
6. В чем разница между параметрами угловой скорости, записанной в форме кососимметрической матрицы, и той же скорости, записанной в виде матрицы- столбца?
СПИСОК ЛИТЕРАТУРЫ
1. Айзерман М.А. Классическая механика. – М.: Наука,1974, с.368.
2. Бранец В.Н., Шмыгловский И.П. Применение кватернионов в задачах ориентации твердого тела. – М.: Наука, 1973. 320 с.
3. Бромберг П.В., Михалев И.А., Никитин Е.А., Бауман В.А., Балашова А.А. Гироскопические системы. ч. II. Гироскопические приборы и системы. Под ред. Д.С. Пельпора.- М.: Высшая школа, 1971. – 488 с.: ил.
4. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1965, 608 с.
5. Зенкевич С.Л., Ющенко А.С. Основы управления манипуляционными роботами: Учебник для вузов.– 2-е изд., исправ. и доп.– М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.- 480 с. ил.
6. Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. – М.,"Наука",1976, с.672.
7. Литвин – Седой М.З. Введение в механику управляемого полета.– М.: Высшая школа,1962, с. 212.
8. Одинцов А.А., Павловский М.А., Бублик Г.Ф., Евгеньев В.С., Бондарь П.М. Теория гироскопов и гироскопических приборов. Практикум. К.: Высшая школа, 1976.
9. Робототехника и гибкие автоматизированные производства. В 9-ти кн. Кн. 5. Моделирование робототехнических систем и гибких автоматизированных производств. Учеб. пособие для вузов/ С.В. Пантюшин, В.М. Назаретов, О.А. Тягунов и др.; Под ред. И.М.Макарова. – М.: Высшая школа,1986.–175 с.: ил.
ПОТАПОВ Анатолий Андреевич
ПАРАМЕТРЫ УГЛОВОЙ ОРИЕНТАЦИИ ПОДВИЖНЫХ ОБЪЕКТОВ:
ПРИКЛАДНЫЕ ЗАДАЧИ
