Постановка физической задачи
Отвод дымовых газов осуществляется через дымовую трубу высотой 100м с диаметром устья 6м. На ГРЭС-2 сжигается уголь Кузнецкого угольного бассейна. Средняя зольность угля, сжигаемого на Томской ГРЭС-2, составляет 17,0%, содержание серы – 0,35%, азота – 1,75%, массовая доля минеральных примесей – 2–4%, калорийность угля – 5160 ккал/кг.
Рассматриваемая область 150x300м. Время расчета 10 мин. Загрязняющее вещество диоксид серы – соединение серы с кислородом состава SO2. В нормальных условиях представляет собой бесцветный газ с характерным резким запахом. ПДК содержания серы в воздухе рабочей зоны – 10 мг/м3. Необходимо исследовать зависимость изменения концентрации диоксида серы в зависимости от скорости ветра, значения которой задаем в диапазоне от 1 до 5 м/с.
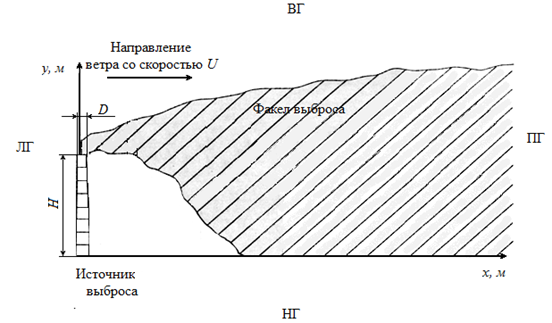
Н – высота трубы; D – диаметр устья; ВГ – верхняя граница; ЛГ – левая граница; НГ – нижняя граница; ПГ – правая граница.
Рисунок 2 – Схема расположения источника выброса
Постановка математической задачи
В качестве математической модели решения задачи используем дифференциальное уравнение (1):
ρ 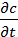 + u
+ u 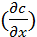 + u
+ u 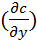 =
= 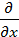 ( ρ
( ρ 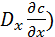 +
+ 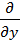 (
( 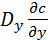 ) + S (1)
) + S (1)
где,
ρ – плотность загрязняющего вещества;
Dx,y – коэффициент диффузии на оси x, y;
u, – профили скорости ветра на оси х, y;
S – источник загрязняющего вещества;
Начальные условия:
С 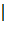 t=0 = 0 (Сф)
t=0 = 0 (Сф)
Граничные условия:
ЛГ: С 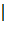 х=0 = 0
х=0 = 0
ПГ: 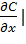 х=х¥ = 0
х=х¥ = 0
НГ: С 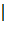 y=0 = 0
y=0 = 0
ВГ: 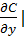 y=y¥ = 0
y=y¥ = 0
Задаем источник:
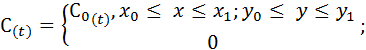
Метод решения
Наилучшим методом для получения консервативной системы уравнений является метод контрольного объема, смысл которого заключается в следующем: геометрическое и временное пространство разбивается на конечное число объемов, затем для каждого из них записывается баланс субстанции (энергии, импульса, массы и т.д.), т.е. разница величины рассматриваемой вами субстанции поступившей и покинувшей данный объем за определенный промежуток времени (интервал).Что самое важное в расчете, это то, что баланс для каждого контрольного объема в общем случае связан с балансом еще шести смежных с ним объемов. В расчетной области требуется установить граничные условия. Полученная после система алгебраических уравнений решается итерационным способом, далее результаты решения обрабатываются и представляются в удобном для анализа виде. Классический метод конечных (контрольных) объемов (FiniteVolumesMethod (FVM); МКО) основан на интегральных законах сохранения. На первом этапе для любого конечного объема формулируется закон сохранения. Затем расчетная область покрывается сеткой, в узлах которой будут рассчитываться физические характеристики (параметры) моделируемого процесса. Далее выбираются контрольные объемы, чаще всего, с центрами в узлах расчетной сетки и границами, проходящими через центры ребер ячеек сетки. Для каждого полученного контрольного объема записывается дискретный аналог закона сохранения на основе баланса всех потоков через границы рассматриваемого объема. Метод конечных объемов в большинстве случаев позволяет получать консервативные схемы, допускает дискретизацию расчетных областей со сложной геометрией, а также позволяет строить более точные схемы вблизи границ области. Эти достоинства метода обусловлены возможностью использовать нерегулярные сетки, равно как и контрольные объемы произвольной формы.
Выбор данного метода дискретизации объясняется тем, что, используя его, в процессе решения точно выполняются интегральные законы сохранения таких величин как масса, количество движения, энергия в каждом контрольном объеме и для любой группы контрольных объемов и, следовательно, на всей расчетной области. Даже если решается задача с использованием малого количества контрольных объемов (тут ограничением могут являться возможности вычислительной техники) все равно решение будет получено, и оно будет удовлетворять точным интегральным балансам во всей расчетной области. Используя в решении метод контрольного объема при правильно заданных граничных условиях можно наверняка сказать, что будет получено физически оправданное решение, которое будет удовлетворять основным законам сохранения, т.к. был использован именно данный метод построения дискретного аналога для дифференциальных уравнений.
Дифференциальные уравнения, описывающие процессы тепло- и массообмена и гидродинамики подчиняются обобщенному закону сохранения. Если обозначить любую искомую функцию Ф, то обобщенное дифференциальное уравнение принимает в тензорной форме вид (формула 2):
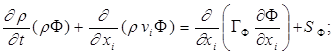 (2)
(2)
где t, – временная координата, xi– и пространственная координата, ρ – плотность, vi – компоненты вектора скорости, ГΦ– коэффициент переноса (например, ГΦ – коэффициент турбулентной вязкости, теплопроводности, диффузии и т.д.), SΦ – источниковый член. В частности, в SΦ может входить приток (сток) тепла за счет химических реакций в уравнении энергии или увеличение (уменьшение) концентраций компонент в результате химических реакций в уравнении диффузии. Конкретный вид ГΦ и SΦ зависит от смысла переменной Ф.
Физически метод контрольного объема можно описать следующим образом: расчетная область разбивается на определенное число непересекающихся контрольных объемов таким образом, что каждая узловая точка содержится в одном контрольном объеме. В двумерном случае мы рассматриваем прямоугольник. Далее, дифференциальные уравнения интегрируются по каждому контрольному объему. Для вычисления интегралов используются кусочные профили, которые описывают изменение функции Ф между узловыми точками. Полученный дискретный аналог выражает закон сохранения для параметра состояния Ф для каждого конечного контрольного объема. Важнейшее свойство метода контрольного объема состоит в том, что при его использовании точно выполняются интегральные законы сохранения таких величин как масса, количество движения, энергия и т.д. в каждом контрольном объеме и для любой группы контрольных объемов и, следовательно, на всей расчетной области. Решение с использованием малого количества контрольных объемов также удовлетворяет точным интегральным балансам во всей области, то есть дискретный аналог (разностная схема) Патанкара-Сполдинга является консервативным. Способ разбиения расчетной области для двухмерного случая на контрольные объемы и типичный контрольный объем представлены на рисунке 3 [7].
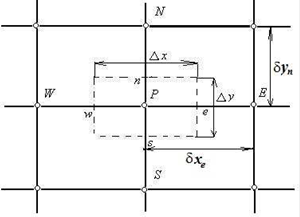
Рисунок 3 – Типичный контрольный объем для двухмерного случая
На рисунке изображена область двухмерной сетки, где пунктирной линией обозначен контрольный объем для двухмерной области с центром в точке P. Центры соседних контрольных объемов обозначены буквами N, S, W, E (соответственно «север», «юг», «запад» и «восток»). Соответствующие точки на границах контрольного объема обозначены буквами n, s, w, e. Размеры контрольного объема обозначаются Δx и Δy. Расстояния до центров соседних контрольных объемов обозначены δxe, δyn.Таким же образом по аналогии вводятся обозначения трехмерного (пространственного) случая, то есть для контрольного объема, изображенного на рисунке.
Дискретный аналог для двухмерного случая запишется в следующем виде (формула 3):
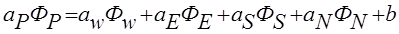 , (3)
, (3)
где: 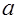 Е = DeA(|Pe|)+[|-Fe, 0|];
Е = DeA(|Pe|)+[|-Fe, 0|]; 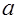 W = DwA(|Pw|)+[|-Fw, 0|];
W = DwA(|Pw|)+[|-Fw, 0|]; 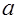 N = DnA(|Pn|)+[|-Fn, 0|];
N = DnA(|Pn|)+[|-Fn, 0|]; 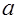 S = DsA(|Ps|)+[|-Fs, 0|]; b = SΔxΔy+
S = DsA(|Ps|)+[|-Fs, 0|]; b = SΔxΔy+ 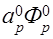 ;
; 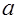 p =
p = 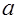 E+
E+ 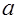 W+
W+ 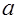 N+
N+ 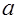 S+
S+ 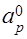 –SpΔxΔy;
–SpΔxΔy; 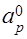 =
= 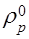 ΔxΔy / Δt.
ΔxΔy / Δt.
Расходы (F) и проводимости (D) определяются следующим образом (формула 4):
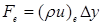 ;
; 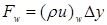 ;
; 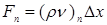 ;
; 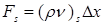 ;
;
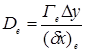 ;
; 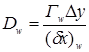 ;
; 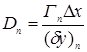 ;
; 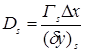 . (4)
. (4)
а числа Пекле (формула 5):
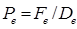 ;
; 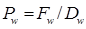 ;
; 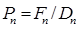 ;
; 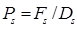 . (5)
. (5)
Выражение типа [A, B] означает, что выбирается максимальный элемент из двух. Для функции A(|P|) рекомендуется схема со степенным законом (формула 6).
A(|P|) = [|0,(1-0,1|P|)5|]. (6)
Коэффициенты в соседних точках 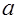 Е,
Е, 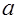 W,
W, 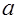 N,
N, 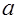 S, учитывают влияние конвекции и диффузии для граней контрольного объема, которые в свою очередь зависят от массового расхода F и проводимости D.Член ароФро характеризует известную величину Ф для контрольного объема (для времени t), отнесенную к шагу по времени. Оставшиеся члены можно интерпретировать аналогичным образом.
S, учитывают влияние конвекции и диффузии для граней контрольного объема, которые в свою очередь зависят от массового расхода F и проводимости D.Член ароФро характеризует известную величину Ф для контрольного объема (для времени t), отнесенную к шагу по времени. Оставшиеся члены можно интерпретировать аналогичным образом.
Для решения дискретного аналога был использован алгоритм Томаса или TDMA (Tri-diagonal-Matrix Algorithm – трехдиагональный матрицы алгоритмом). Название TDMA является результатом того, что когда матрица коэффициентов этих уравнений записана, все ненулевые коэффициенты группируются вдоль трех диагоналей матрицы.
Для удобства записи алгоритма введем некоторые обозначения. Присвоим узловым точкам номера 1, 2, 3, ..., n. Номера 1 и n относятся к точкам на границе. Тогда дискретный аналог можно записать в следующем виде (формула 7):
aiTi = biTi+1+ ciTi-1 + di, (7)
где i = l, 2, 3, ..., n. Таким образом, температура Т, связана с соседними значениями Ti-1 и Тi+1.
Запись уравнений для узловых точек на границе дает (формула 8):
c1 = 0; bn = 0. (8)
Следовательно, температуры Т0 и Тn+1 не будут, иметь, смысла (в том случае, когда температуры на границе заданы, уравнения для граничных точек записываются в обычной форме, например, если T1 задано, имеем а1 b1 = 0, c1 = 0 и d1 равно заданному значению Т1). [7]
