Работа, энергия. Законы сохранения

3.1. 1.177. Шарик массой 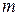надо медленно поднять на высоту Н за пружинку жёсткостью 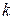. Какую работу надо при этом совершить?

Ответ. A=k(Dx)² /2+mgH, где Dх=F_упр/k=mg/k – деформация пружины.

3.2. 1.180. Бегун на старте достигает скорости 10 м/с за 4 с. Найти среднюю мощность, развиваемую бегуном на старте, если его масса 80 кг.

Ответ. 1 кВт.

3.3. 1.197. Шарик бросили вертикально вверх со скоростью υ₀=20 м/с. На какой высоте его кинетическая энергия будет равна потенциальной?

Ответ. 10 м.

3.4. 1.198. Шарик бросили под углом 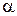к горизонту. Найти отношение потенциальной энергии к кинетической в верхней точке его траектории.

Ответ. W_п/W_к=tg² a.

3.5. 1.199. Шарик бросили с земли со скоростью υ₀ под углом α к горизонту. Определить его скорость υ на высоте h.

Ответ. υ= ; скорость υ от угла a не зависит.

3.6. 1.200. С одинаковой высоты бросили 4 шарика: первый просто отпустили, а начальные скорости других показаны на рисунке (они отличаются только по направлению). Определить соотношения равенства или неравенства между модулями скоростей шариков у поверхности земли.

3.7. 1.201. Два шарика летят навстречу друг другу по оси х и происходит их прямой удар. Массы шариков 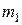=1 кг, 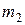=2 кг, а их скорости 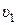=1 м/с (вправо), υ₂=2 м/с (влево). Определить: а) скорость шаров u_x после их абсолютно неупругого удара; б) скорости шаров u_1x и u_2x после их абсолютно упругого удара.

Ответ. u=–1 м/с; u₁=–3 м/с, u₂=0.

3.8. 1.203. Два человека массами m₁=60 кг и m₂=80 кг отталкиваются друг от друга на льду. Один из них проехал до полной остановки путь s₁=16 м. Сколько проедет другой, если их коэффициенты трения о лед постоянны и одинаковы?

Ответ. 9 м.

3.9. 1.207. Один шар неподвижен, а другой налетает на него. После прямого абсолютно упругого удара шары разлетаются в противоположных направлениях с одинаковыми скоростями. Найти отношение масс шаров.

Ответ. 3.

3.10. 1.209. Пуля массой 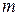=4 г, летящая горизонтально, попадает в шар массой М=800 г, висящий на нити длиной =90 см, и застревает в нём. Шар отклонился на угол . Вычислить скорость пули υ₀.

Ответ. 600 м/с.

3.11. 1.210. Пуля массой 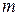=4 г, летящая горизонтально, пробила висящий на нити шар массой М=400 г, и он отклонился на угол α=60°. Длина нити l=0,9 м, входная скорость пули υ₁=600 м/с. Вычислить выходную скорость пули υ₂ .

Ответ. 300 м/с.

3.12. 1.216.Ведро с водой вращается в вертикальной плоскости на верёвке длиной м. Определить: а) минимальную скорость ведра в верхней точке траектории; б) соответствующую скорость ведра в нижней точке; в) натяжение веревки внизу, если масса ведра с водой кг.

Ответ. , , 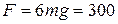Н.

3.13. 1.221. Шарик массой 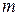подвешен на нити, способной выдержать вес 2mg. На какой угол надо отклонить шарик, чтобы он оборвал нить, проходя через нижнее положение?

Ответ. 60°.

3.14. 1.232.Частица соскальзывает без начальной скорости с вершины гладкой горки, плавно переходящей в круглый гладкий жёлоб радиусом (см. рис.). Определить минимальную высоту горки , при которой частица пройдет по всему жёлобу, не оторвавшись от него.

Ответ. h=2,5R.

3.15. 1.234. Частица соскальзывает без начальной скорости с вершины гладкой горки высотой , имеющей горизонтальный трамплин (см. рис.). При какой высоте трамплина частица пролетит максимальное расстояние 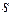и чему оно равно?

Ответ. h=Н/2, s=H.