Теоретические сведения. ЛАБОРАТОРНАЯ РАБОТА №4 ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ
ЛАБОРАТОРНАЯ РАБОТА №4 ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ...6
ЛАБОРАТОРНАЯ РАБОТА №5 ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ…………………………………………………………12
ЛАБОРАТОРНАЯ РАБОТА №6 ИЗУЧЕНИЕ ЗАКОНА МАЛЮСА…...……20
ЛАБОРАТОРНАЯ РАБОТА №7 ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА ОПТИЧЕСКИ АКТИВНЫМИ ВЕЩЕСТВАМИ….24
ЛАБОРАТОРНАЯ РАБОТА №8 МАГНИТНОЕ ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА…………………………………………………………….31
ЛАБОРАТОРНАЯ РАБОТА №9 КАЧЕСТВЕННЫЙ СПЕКТРАЛЬНЫЙ АНАЛИЗ………………………………………………………………………………...37
ЛАБОРАТОРНАЯ РАБОТА №10 ЗАКОНЫ ТЕПЛОВОГО ИЗЛУЧЕНИЯ…42
ЛАБОРАТОРНАЯ РАБОТА №11 ИЗУЧЕНИЕ ЯВЛЕНИЯ ФОТОЭФФЕКТА С ПОМОЩЬЮ ВАКУУМНОГО ФОТОЭЛЕМЕНТА……………………………50
ЛАБОРАТОРНАЯ РАБОТА №12 ОПРЕДЕЛЕНИЕ МАССЫ ЭЛЕКТРОНА И РАДИУСА ПЕРВОЙ БОРОВСКОЙ ОРБИТЫ АТОМА ВОДОРОДА…………56
ЛАБОРАТОРНАЯ РАБОТА №14 ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ И ДИСПЕРСИИ ОПТИЧЕСКИ ПРОЗРАЧНЫХ СРЕД…...63
ЛАБОРАТОРНАЯ РАБОТА №15 ОПРЕДЕЛЕНИЕ ШИРИНЫ ЗАПРЕЩЕННОЙ ЗОНЫ ПОЛУПРОВОДНИКА…………………………………74
ЛАБОРАТОРНАЯ РАБОТА №16 ИЗУЧЕНИЕ ФОТОРЕЗИСТОРОВ…….....91
ЛАБОРАТОРНАЯ РАБОТА 3
ОПРЕДЕЛЕНИЕ РАДИУСА КРИВИЗНЫ ЛИНЗЫ С ПОМОЩЬЮ КОЛЕЦ НЬЮТОНА
Ц е л ь р а б о т ы: Изучить явление интерференции света и определить радиус кривизны линзы.
О б о р у д о в н и е : Источник монохроматического света; линза плосковыпуклая; пластинка плоскопараллельная; микроскоп измерительный.
Теоретические сведения
Одним из проявлений интерференции являются так называемые кольца Ньютона – кольцеобразные интерференционные полосы, образующиеся при падении (прохождении) света на воздушную или жидкую прослойку, разделяющие две сферические или сферическую и плоскую поверхности.
Интерференционная картина, возникающая в такой системе, представляет собой интерференцию равной толщины, так как кольцевые интерференционные полосы соответствуют определенной толщине прослойки между поверхностями.
Рассмотрим прохождение монохроматического света через систему, состоящую из плотно прижатых друг к другу плоскопараллельных пластин и плосковыпуклой линзы.
Место соприкосновения стекла с линзой окружено системой концентрических темных и светлых колец. Они видны как в проходящем, так и в отраженном свете. Кольца Ньютона в отраженном свете образуются за счет интерференции колебаний, отраженных от изогнутой поверхности линзы и поверхности пластинки. Обычно световые лучи падают почти по нормали к пластинке, поэтому угол падения близок к нулю и разность хода двух волн равна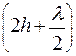 
. Дополнительная разность хода 
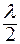получается при отражении от плоской пластинки (рис.4).
Условие максимума интерференции состоит в том, чтобы на разности хода двух волн укладывалось четное число полуволн или целое число длин волн:
.
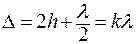Условие минимума интерференции состоит в равенстве разности хода нечетному числу длин волн:
.
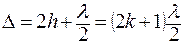Из геометрических законов (рис.4) следует. Что радиус k-го кольца Ньютона rk связан с толщиной воздушного слоя и радиусом кривизны линзы R соотношением
,
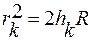где k- номер кольца.
Произведем расчет радиуса кривизны линзы по темным кольцам (выбор колец случаен):
, 
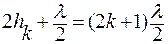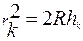откуда 
.
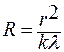Эту формулу можно использовать для определения радиуса кривизны линзы. Для большей точности лучше воспользоваться для расчета двумя кольцами.
Из уравнений (10), (11) получают значения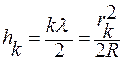 
,
тогда для любого i –го кольца
,
,
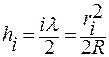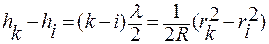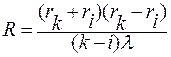или
.
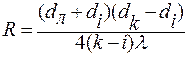Таким образом, измерив диаметры к-го и ш-го колец (например, 5 и 12) и зная длину световой волны, можно по формуле (12) вычислить радиус кривизны линзы.
Для измерения диаметров колец Ньютона используется измерительный микроскоп, тубус которого может перемещаться в направлении, перпендикулярном его оси. Перемещение тубуса производится посредством микрометрического винта. Полный оборот барабана соответствует горизонтальному перемещению тубуса на 1 мм. Отсчет целых делений производится по горизонтальной шкале, сотые доли миллиметра отсчитываются при помощи делений, помещенных на боковой поверхности барабана.
Укрепленную в общей оправе линзу и плоскую стеклянную пластинку помещают на столик микроскопа и освещают монохроматическим светом.