А. Гравитационный дрейф

В этом случае сила 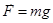- сила тяжести и выражение для скорости дрейфа превращается в следующую формулу:

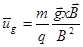(2.1.10)

В этом виде дрейфа скорость его зависит от заряда и массы частицы. Важно, что в случае гравитационного дрейфа ионы и электроны дрейфуют в противоположных направлениях и, тем самым, создается электрический ток, плотность которого выражается формулой (ионы считаем однозарядными):

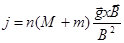(2.1.11)

б. Градиентный дрейф .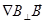

Здесь нам придется столкнуться с пространственной неоднородностью, сильно затрудняющей получение точных решений. Приближенные же ответы получают обычно, применяя так называемый подход слабой неоднородности, то есть проводя разложение по параметру 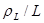(полагаемому малым) , где L – характерный масштаб неоднородности.

По-прежнему считаем магнитное поле направленным вдоль оси z, а градиент его пусть, для определенности, будет направлен по оси y. Качественно можно сразу сказать, что ларморовский радиус в области больших y будет больше, чем в области меньших y. Это приведет к тому, что дрейф ионов и электронов будет происходить в противоположных направлениях и перпендикулярно, как 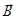, так и 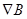. Итак, для нахождения скорости дрейфа мы должны получать силу, усредненную по периоду вращения частицы. В случае градиентного дрейфа усреднять нужно пространственно неоднородную силу Лоренца, 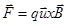. Приближенность нашего рассмотрения обусловлена усреднением по невозмущенной орбите частицы. Такое усреднение даст 0 для x компоненты силы Лоренца, 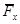=0 (частица движется вверх столько же времени, сколько и вниз). Выражение же для y – компоненты:

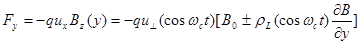, (2.1.12)

где использовано разложение поля в ряд Тейлора 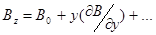, дает при усреднении:

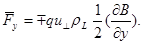(2.1.13)

Таким образом, с учетом произвола при выборе направления градиента магнитного поля, получаем для скорости градиентного дрейфа:

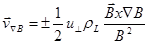(2.1.14)

Формула дает противоположные направления дрейфа ионов и электронов, что приводит к появлению электрического тока ^ магнитному полю.

в. Центробежный дрейф.

При движении плазмы в магнитном поле с искривленными силовыми линиями возникает центробежная сила, которая может быть рассматриваема, как некоторый аналог гравитации. Здесь также оказывается применимой дрейфовая трактовка движения заряженных частиц. Положим для простоты, что радиус кривизны силовых линий магнитного поля постоянен и равен R_c .По той же причине считаем постоянным модуль магнитного поля B=const. Пусть также 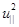- средний квадрат скорости хаотического движения вдоль магнитного поля. Тогда выражение для средней центробежной силы, действующей на частицу

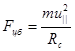(2.1.15)

и, в соответствии с общим выражением для дрейфовой скорости (2.1.9) получаем выражение для центробежного дрейфа:

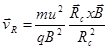(2.1.16)

2.1.4. Магнитная пробка.

Этот случай соответствует условию: 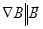. Направим, как и прежде, магнитное поле вдоль оси z, положим его аксиально-симметричным с модулем напряженности, зависящем от z. В этом случае оно будет состоять из двух компонент: продольной B_z и радиальной B_r . Связь между этими компонентами вытекает из условия равенства нулю дивергенции магнитного поля, которое для оговоренного случая выглядит следующим образом:

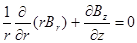(2.1.17)

Пусть производная 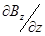задана на оси (при r = 0) и слабо зависит от радиуса. Тогда, проинтегрировав (2.1.17), получаем:

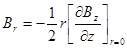(2.1.18)

Для анализа движения частицы в принятых условиях удобно выписать компоненты лоренцевой силы:

,

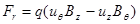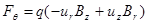, (2.1.19)

.

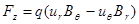Для нашего случая: ( 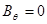) имеем:

,

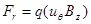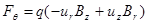, (2.1.20)

.

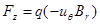Первое из уравнений совместно с первым членом второго описывает ларморовское вращение, изученное нами ранее. Второй член второго уравнения (азимутальная составляющая силы Лоренца), обращаясь в 0 на оси, вызывает дрейф в радиальном направлении, приводящий в результате к движению ведущих центров частиц вдоль кривых силовых линий магнитного поля. Особый интерес представляет для нас в данном случае третье из выражений (2.1.20). Подставив в него B_r из (2.1.18), получим:

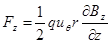2.1.21)

Усредним теперь полученное выражение по периоду вращения частицы, ведущий центр которой находится на оси (для простоты). При этом r = r_L и скорость u_q постоянна. Получаем, что для данного случая, средняя сила, действующая на частицу, описывается выражением:

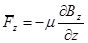(2.1.22)

где величина 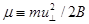определяется как магнитный момент частицы. Для общего случая выражение (2.1.22) может быть переписано, как F_êê= -m 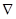_êêB .

Магнитный момент частицы, движущейся в неоднородном магнитном поле, не изменяется, являясь инвариантом движения. Это легко можно показать, рассмотрев проекцию уравнения движения на направление магнитного поля:

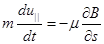(2.1.23)

Помножив (2.1.23) слева на u_êê , а справа на равную величину ds/dt , получаем:

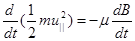(2.1.23)

Здесь dB/dt – изменение поля в системе координат движущейся частицы. Запишем теперь закон сохранения полной кинетической энергии частицы:

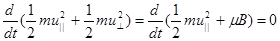(2.1.24)

Откуда, используя (2.1.23), получаем:

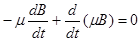, и, следовательно, 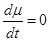(2.1.25)

На сохранении магнитного момента движущейся в магнитном поле заряженной частицы основывается идея магнитной пробки. Частица, двигаясь в область сильного магнитного поля при сохранении магнитного момента, увеличивает скорость поперечного вращения. В соответствии с законом сохранения энергии, скорость продольного движения должна уменьшатся.

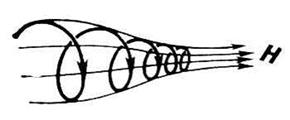
Рис. 2.3. Магнитная пробка (зеркало).

При достаточно большом поле в «пробке», найдется место, где продольная скорость обратится в нуль и произойдет отражение частицы. Расположив две «пробки» одну напротив другой, получим магнитную ловушку, называемую обычно «пробкотроном» или зеркальной ловушкой.

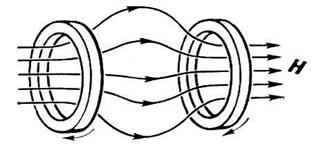
Рис.2.4. Магнитная конфигурация «пробкотрона»

2.1.5. Движение в неоднородном электрическом поле.

Рассмотрим теперь влияние неоднородности электрического поля. Магнитное поле пусть будет однородным и постоянным; сохраним за ним прежнее направление – вдоль оси z.

Электрическое поле зададим в виде поля плоской стоячей электростатической волны длиной 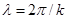, волновой вектор которой направлен вдоль оси x.:

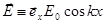(2.1.26)

Поскольку движение вдоль магнитного поля здесь нас не интересует, выпишем сразу поперечные компоненты уравнения движения частицы:

а) 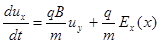; б) 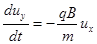(2.1.27)

Или, продифференцировав вторично по времени, перепишем их в виде:

а) 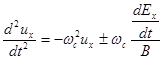; б) 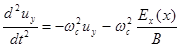(2.1.28)

Чтобы знать величину электрического поля в месте нахождения частицы, нужно знать ее траекторию. В нулевом приближении по электрическому полю эта траектория нам известна – ларморовское вращение в однородном магнитном поле вокруг ведущего центра: 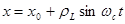. Используем ее .Подставив электрическое поле из (2.1.26) в уравнение (2.1.28.б) , получим с учетом невозмущенной траектории частицы:

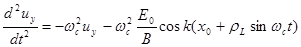(2.1.29)

Поскольку нас интересует дрейфовая составляющая скорости, усредним уравнения движения по периоду циклотронного вращения частицы. Все осциллирующие члены при этом «зануляются». Поэтому из уравнения (2.1.28а) видно, что средняя составляющая x – компоненты скорости оказывается равной нулю, а из уравнения для y-компоненты скорости получается следующее выражение:

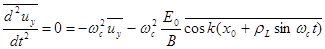(2.1.30)

Отсюда нетрудно выразить среднюю скорость по направлению y :

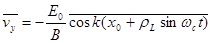(2.1.30)

Далее, воспользовавшись тригонометрическими преобразованиями и возможностью ограничиться малыми значениями ларморовского радиуса (kr_L<<1 ; при этом используем старшие члены разложения тригонометрических функций в ряд Тейлора : sina @ a , cosa @ 1-(1/2) a² ), получаем, помня об исчезновении при усреднении осциллирующих членов, следующее выражение:

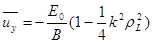, (2.1.31)

которое, в общем виде, может быть переписано следующим образом:

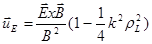. (2.1.32)

Если пространственная неоднородность поля имеет произвольный вид, то оно трансформируется (k меняется на ):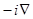

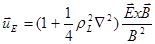. (2.1.33)

Итак, при наличии неоднородности электрического поля обычное выражение для скорости дрейфа в скрещенных полях (см.(2.1.8)) изменяется с учетом поправки, величина которой зависит от соотношения характерного размера неоднородности и ларморовского радиуса. Таким образом поправка учитывает эффект конечного ларморовского радиуса при дрейфовом движении. Очевидно, что при этом возникает различие в дрейфе электронной и ионной компонент плазмы, что ведет к разделению зарядов. Это значит, что наличие неоднородного электрического поля в плазме запускает в действие механизм возникновения вторичного электрического поля, что может явиться причиной, как развития неустойчивости, так и ее стабилизации в зависимости от знака возникающего вторичного поля.

2.1.6. Нестационарное электрическое поле.

Пусть теперь, при пространственной однородности электрического и магнитного полей, магнитное поле постоянно, а электрическое поле меняется во времени по синусоидальному закону и имеет только x-компоненту:

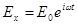(2.1.34)

При этом компоненты дрейфового движения может быть записаны в виде:

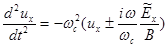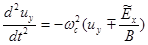, (2.1.35)

Если ввести теперь величины:

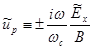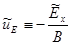, (2.1.36)

то интересующие нас компоненты уравнения движения принимают вид:

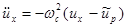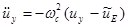, .(2.1.37)

Решение системы .(2.1.37) ищем в виде:

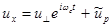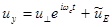, . (2.1.38)

Для этого дважды продифференцируем выражения (2.1.38) по времени и сравним с .(2.1.37). Дифференцирование дает:

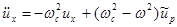; (2.1.39а)

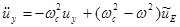(2.1.39б)

Выражения (2.1.39) совпадают с .(2.1.37), если w² мало по сравнению с 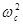.Это означает, что предложенная нами модель решения – быстрое вращение, наложенное на сравнительно медленный дрейф ведущего центра может быть принята при сравнительно медленных изменениях электрического поля. Трактовка введенных нами в (2.1.36) величин такова: скорость дрейфа ведущего центра может быть представлена двумя медленно (по сравнению с циклотронным вращением) осциллирующими составляющими. В направлении y - это обычный дрейф в скрещенных электрическом и магнитном полях, а в направлении x – новый тип дрейфового движения – вдоль электрического поля. Это, так называемый, поляризационный дрейф, возникающий при любом изменении электрического поля. Обобщенное выражение для скорости поляризационного дрейфа получается посредством замены в первой из формул (2.1.36) 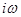на :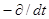

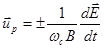(2.1.40)

Скорости поляризационного дрейфа для электронов и ионов направлены в противоположные стороны, следовательно, дрейфовое движение этого типа вызывает поляризационный ток:

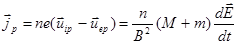(2.1.41)

2.1.7. Движение в нестационарном магнитном поле

Изменяющееся во времени магнитное поле вызывает появление электрического поля

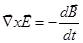(2.1.42)

которое способно (в отличие от магнитного ) изменять энергию частицы:

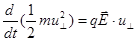, (2.1.43)

Рассматриваем здесь только поперечное движение; 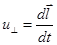; 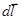- элемент траектории частицы. Изменение энергии частицы за один оборот получим, проинтегрировав (2.1.43) по периоду вращения:

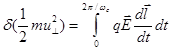, (2.1.44)

Считая, что поле меняется достаточно медленно, будем интегрировать вдоль невозмущенной орбиты:

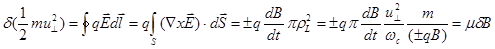.(2.1.45)

Здесь учтено, что 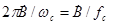- изменение за один оборот. Так как . приращение кинетической энергии частицы тождественно равно 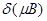, то из (2.1.45) следует

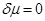(2.1.46)

Таким образом, мы получаем инвариантность магнитного момента в медленно меняющемся магнитном поле. Отсюда следует еще одно утверждение: Магнитный поток через поверхность, ограниченную ларморовской окружностью, постоянен. Действительно:

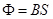, где 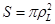, поэтому 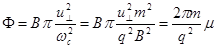(2.1.47)

откуда видно, что если 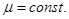, то и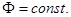

2.1.8 .Адиабатические инварианты.

Как известно, в классической системе при наличии периодического движения сохраняется интеграл 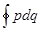, взятый по периоду движения. (p и q –обобщенные импульс и координата). Если движение системы не является строго периодическим, но изменения достаточно медленны (происходят за времена, много большие периода), то выписанный выше интеграл движения по-прежнему сохраняется; в этом случае он называется адиабатическим инвариантом. В физике плазмы адиабатические инварианты, связанные с различными типами периодических движений, играют важную роль. Укажем на некоторые из них.

а) Первый адиабатический инвариант. Это уже рассматривавшийся нами магнитный момент вращающейся частицы:

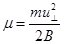
Этот инвариант соответствует ларморовскому вращению и, как было показано выше, сохраняется в нестационарных и неоднородных магнитных полях. Условием адиабатичности в данном случае является неравенство 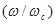<<1.

б) Второй адиабатический инвариант.. Другим периодическим движением, важным для изучения движений плазмы в магнитных ловушках, является осцилляция частиц, захваченных между двумя пробками. В этом случае интегралом движения является интеграл 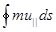, где ds – элемент длины дуги при движении ведущего центра вдоль силовой линии. Этом интеграл называется продольным инвариантом J и вычисляется между точками отражения:

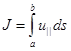
Условием адиабатичности здесь является медленность изменений по сравнению с баунс-периодом. 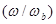<<1. Здесь w_b - Баунс-частота – частота осцилляций между пробками.

в) Третий адиабатический инвариант. Нестрогость периодичности осцилляций между пробками связана, в частности, с азимутальным дрейфом частиц в пробкотроне. Это движение, в свою очередь, является периодическим и с ним связывается третий адиабатический инвариант – полный магнитный поток, охватываемый дрейфовой поверхностью Ф. Этот инвариант обычно менее полезен в технических приложениях. Дело в том, что он связан с относительно медленным движением; многие, интересные с точки зрения удержания плазмы в ловушке процессы, протекают быстрее, чем нужно для сохранения адиабатичности процесса. Однако, скажем, в геофизике его удобно использовать при изучении движения заряженных частиц в радиационных поясах Земли

2.2. Гидродинамический подход.

2.2.1. Одножидкостная гидродинамика.

В рамках этой модели плазма рассматривается как проводящая жидкость. При этом в обычное гидродинамическое уравнение движения среды кроме силы, связанной с градиентом давления, вязкостью и т.д., добавляется пондеромоторная сила:

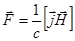(2.2.1)

где 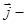плотность тока, 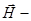напряженность магнитного поля.

Если пренебречь вязкостью и другими диссипативными силами, то уравнение движения проводящей жидкости имеет вид:

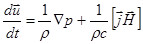(2.2.2)

где 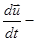ускорение рассматриваемого «элемента жидкости». Уравнение(2.2.2) написано в представлении Лагранжа, когда движение жидкости изучается путем слежения за траекторией выбранного элемента и, выписанная выше производная, является производной вдоль траектории; ее называют лагранжевой производной. Существует альтернативный подход, называемый представлением Эйлера, при котором рассматривается изменение скорости среды в выбранной точке пространства : 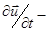эйлерова производная. Хотя она и является производной скорости по времени, но не имеет физического смысла ускорения. Связь между лагранжевой и эйлеровой производными дается выражением:

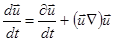
Поэтому уравнение (2.2.2) в представлении Эйлера будет выглядеть следующим образом:

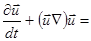
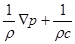
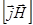(2.2.2а)

Плотность тока задается законом Ома:

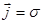
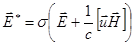(2.2.3)

где 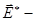напряженность электрического поля в системе отсчета, движущейся вместе с плазмой, 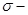проводимость плазмы, 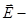напряженность электрического поля в лабораторной системе координат.

Задание плотности тока с помощью закона Ома, при том, что проводимость плазмы считается константой - главный недостаток одно-жидкостной МГД теории. Во многих случаях этот подход неприменим, однако имеется достаточно много практически интересных случаев, когда такое упрощение является оправданным.

Система уравнений (2.2.2) – (2.2.3), описывающая движение плазмы, должна быть дополнена уравнениями Максвелла. Совместное их решение и составляет обсуждаемый подход к исследованию плазмы. Дополнительное существенное упрощение модели получается, если иметь в виду относительную медленность процессов, описываемых данным приближением, что позволяет пренебречь токами смещения. Тогда из всей системы уравнений Максвелла остается лишь:

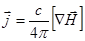(2.2.4)

и уравнение (2.2.2) принимает вид

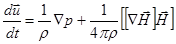(2.2.5)

Используя известное соотношение векторного анализа:

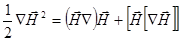(2.2.6)

получим из него:

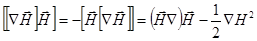(2.2.7)

и, подставив затем (2.2.7) в (2.2.5), имеем:

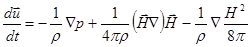(2.2.8)

Правая часть уравнения (2.2.8) содержит три члена, описывающие действие сил, связанных с градиентом давления, кривизной силовых линий и пространственным изменением модуля напряженности магнитного поля. Если магнитное поле меняется только в направлении, поперечном по отношению к силовым линиям, то второй член в правой части, связанный с кривизной силовых линий, обращается в нуль и уравнение может быть переписано в следующем виде:

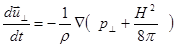(2.2.9)

Здесь 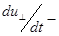ускорение в направлении поперек силовых линий магнитного поля. Член 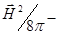входит в формулу на равных основаниях с газокинетическим давлением (поперечным) 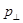, поэтому его также можно интерпретировать как давление – давление магнитного поля. Таким образом, полученное выражение позволяет сделать практически важный вывод о возможности оказывать давление на плазму (проводящую среду) с помощью магнитного поля.