Основные формулы. атомная физика

Атом водорода

Первый постулат Бора. Атомы могут длительно пребывать только в таких состояниях, находясь в которых они не излучают энергии. Этим стационарным состояниям соответствуют определенные энергии Е_1, Е₂, … Е_n атома.

Второй постулат Бора. При переходе из одного стационарного состояния в другое атом испускает или поглощает излучение строго определенной частоты, определяемой условием

hν = E_m – E_n.

Стационарным состояниям атома соответствуют вполне определенные орбиты, по которым движутся электроны. Момент импульса (количества движения) L электрона для стационарных орбит кратен .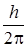

Радиусы круговых орбит электрона определяются равенством

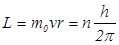, где r – радиус орбиты; v – скорость электрона на этой орбите; n – целое число, называемое квантовым числом (n = 1, 2, 3, …).

Энергия электрона, находящегося на n – й орбите: .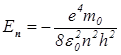

Длина волны λ света, излучаемого атомом водорода при переходе с одной орбиты на другую, может быть определена из сериальной формулы

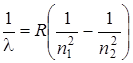, где R – постоянная Ридберга; n₁ и n₂ – квантовые числа, определяющие номера орбит электрона.

Энергия кванта света, излучаемого атомом водорода при переходе с одной орбиты на другую, 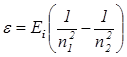, где Е_i – энергия ионизации атома водорода: Е_i = -13,6 эВ.

Энергия ионизации, выраженная в электрон-вольтах, численно равна потенциалу ионизации, выраженному в вольтах. Потенциалом ионизации называется ускоряющая разность потенциалов, которую должен пройти бомбардирующий электрон, чтобы приобрести кинетическую энергию, достаточную для ионизации атома.

Волны де Бройля

Формула де Бройля. Длина волны λ, связанная с частицей, обладающей импульсом р, выражается равенством .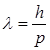

Так как импульс р в классическом приближении (v<<c) выражается формулой p = m₀v, то 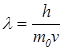, где m₀ – масса покоя частицы.

В релятивистском случае, когда скорость частицы сравнима со скоростью света в вакууме, импульс 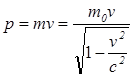. Тогда .

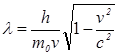Иногда при вычислениях длины волны де Бройля импульс р частицы удобно выражать через ее кинетическую энергию Т. При этом следует пользоваться соотношением 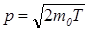, в релятивистском случае 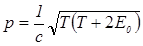, где Е₀ – энергия покоя частицы (Е₀ = m₀c²).

Радиоактивность

Основной закон радиоактивного распада: число нераспавшихся атомов в образце радиоактивного изотопа уменьшается со временем экспоненциально: N = N₀e^-λt, где N – число нераспавшихся атомов в момент времени t; N₀ – число нераспавшихся атомов в момент, принятый за начальный (t = 0); е – основание натуральных логарифмов; λ – постоянная радиоактивного распада.

Число атомов, распавшихся за время t: N₀ – N = N₀(1 – e^-λt).

Если промежуток времени Δt очень мал по сравнению с периодом полураспада Т_1/2, то для определения числа распавшихся атомов служит приближенная формула ΔN ≈ λNΔt.

Период полураспада Т_1/2 – промежуток времени, за который число не распавшихся атомов уменьшается в два раза. Период полураспада связан с постоянной распада соотношением .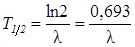

Среднее время жизни τ радиоактивного нуклида – промежуток времени, за который число не распавшихся атомов уменьшается в е раз: .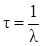

Число атомов, содержащихся в образце нуклида: 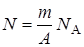, где m – масса образца; А – масса килограмм - атома нуклида; N_A – число Авогадро.

Активность а образца измеряется числом ядер, распавшихся в единицу времени: 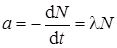или после замены N : а = λN₀ e^-λt.

Активность образца в начальный момент (при t = 0) а₀ = λN₀.

Активность образца изменяется со временем по тому же закону, что и число не распавшихся ядер а =а₀ е^-λt.