Показатель преломления

где c - скорость света.

Если фазовая скорость не зависит от частоты, то групповая ско­рость численно равна фазовой.

Чтобы определить u_ф и u_гр и по направлению, вводят волновой вектор , длина которого равна волновому числу, а направление определено таким образом, чтобы в плоской волне любая величина f зависела от координат и времени как

(4.1.4а)

Направление фазовой скорости есть направление волнового вектора, то-есть направление, в котором распространяется определенная фаза волны.

В анизотропной среде частота связана не только с величиной, но и с направлением волнового вектора, т.е. дисперсионные уравнения имеют вид:

где k₁, k₂, k₃ - составляющие волнового век­тора.

В результате дифференцирования этого уравнения имеем:

u₁, u₂, u₃ имеют размерность скорости и рассматриваются как состав­ляющие вектора групповой скорости. В векторной форме:

Символически это записывают следующим образом

Направление u_гр - есть направление переноса энергии волной. Оси координат обычно выбирают так, чтобы k_z=0. Тогда k₁ - составляющая по нормали к магнитному полю, k₃ - вдоль поля.

В линейном приближении уравнения для комплексных амплитуд имеют тот же вид, что и для f.

Для плоской волны дифференциальные операторы превращаются в алгебраические действия:

Тогда вместо (4.1.3) имеем:

(4.1.5)

Таким образом, подставив в волновое уравнение (4.1.3) решение в виде плоской волны, мы получили дисперсионное уравнение (4.1.5), в котором влияние плазмы на волновой процесс учитывается, неопределенной пока, плотностью тока. Чтобы получить самосогласованную систему уравнений, нужнодобавить описание движения среды (плазмы) под действием поля.

Уравнения движения электронов и ионов без учета столкновений и других диссипативных процессов имеют вид:

(4.1.6)

(4.1.7)

Ограничимся рассмотрением только линейных колебаний. Тогда d/dt можно изменить на ¶/¶t и в произведении пренебречь собственным полем волны, т.е. изменить на постоянное внешнее поле .

Преобразуем (4.1.6) и (4.1.7) так, чтобы получить уравнения для массовой скорости

(4.1.8)

и плотности тока

(4.1.9)

здесь мы используем условие квазинейтральности

(4.1.10)

будем пренебрегать массой электрона по сравнению с массой иона M>>m.

Просуммируем (4.1.6) и (4.1.7) с весами n_em и n_iM и получим

(4.1.11)

Вычитание этих же уравнений с пренебрежением членами, содержащими М в знаменателе, дает

(4.1.12)

Система уравнений (4.1.11) - (4.1.12) совпадает с системой уравнений магнитной гидродинамики для идеального проводника, из которых выброшены силы давления. Если ввести обозначения

(4.1.13)

(4.1.14)

(4.1.15)

то (4.1.12) перепишется

(5.1.16)

где - единичный вектор в направлении постоянного внешнего магнитного поля. Для плоской волны вида (4.1.4) уравнения (4.1.11) и (4.1.16) принимают вид:

(4.1.17)

(4.1.18)

Здесь w - круговая частота возмущения.

В последнем уравнении раскрыто двойное векторное произведение по формуле и использовано соотношение

(4.1.19)

Теперь рассмотрение всех типов колебаний холодной плазмы сводится к совместному решению уравнений (4.1.5), описывающего возмущения полей, и (4.1.18)., описывающего движение плазмы и представляющего собой нечто вроде обобщенного закона Ома.

Повторим допущения, сделанные при их выводе:

· Амплитуды всех переменных в волне малы - линейное приближение, что дает возможность пренебречь квадратичными членами;

· Тепловое давление мало (приближение холодной плазмы);

· Пренебрегается диссипативными эффектами (идеальная плазма);

· Отброшены члены ~ m/M.

4.1.2.Волны при отсутствии магнитного поля.

Начнем рассмотрение с наиболее простого случая. Пусть внешнее магнитное поле плазме отсутствует :H₀ = 0

При этом (4.1.18) сводится к простому виду:

(4.1.20)

Из (4.1.5), в свою очередь, получаем

(4.1.21)

Произвольную волну можно разложить на две независимые: Продольную и поперечную . Для продольной и из (4.1.21) следует:

(4.1.22)

Это плазменные колебания на фиксированной частоте - такие только и возможны в холодной плазме.

Для поперечных и из (4.1.21) получаем:

(2.4)

Соотношение(5.1.23)- дисперсионное уравнение для распространения электромагнитных волн в плазме без магнитного поля. Пока выполняется условие распространение волны возможно. Если же частота колебаний в волне становится меньше плазменной частоты, волновое число и показатель преломления становятся мнимыми, т.е. волна отражается от границы плазмы.

Фазовая скорость выражается следующей формулой:

(4.1.24)

В области распространения волны то-есть при частотах. превышающих плазменную , фазовая скорость больше скорости света и стремится к бесконечности при , Групповая скорость:

(4.1.25)

Откуда непосредственно следует:

(4.1.26)

При частотах много больших плазменной волна распространяется как в вакууме (влияние плазмы мало) и обе скорости стремятся к скорости света. При усилении влияния плазмы (при приближении частоты к плазменной) фазовая скорость, как мы видели, стремится к бесконечности, а групповая, как это следует из соотношения (4.1.26), стремится к нулю. Групповая скорость всегда остается меньше скорости света.

4.1.3.Волны при наличии магнитного поля – простейшие случаи.

Система (4.1.5) – (4.1.18) очень сложна для анализа при произвольном направле­нии распространения волн. Рассмотрим пробные случаи.

Возьмем составляющую векторного уравнения (4.1.18) вдоль поля. Так как. , то

(4.1.27)

Составляющая уравнения (4.1.5) вдоль магнитного поля не, содержит в двух случаях: при распространении волны вдоль поля и при расп­ространении ее поперек поля, когда .

В этих двух простейших случаях колебания с электрическим полем, параллельным магнитному, отщепляются, т.е. представляют собой независимые ветви колеба­ний - магнитное поле на эти ветви не действует. В гидродинамике это утверждение точное. В кинетике, вообще говоря, есть особенности вблизи циклотронных частот и их обертонов. Но, если от этого отвлечься, то такие колебания распространяются вдоль магнитного поля так же, как и в его отсутствие. Действительно, для колебаний с , (4.1.5) сводится к виду:

(4.1.28)

что с учетом (4.1.27) дает

(4.1.29)

Это означает, что колебания, поляризованные вдоль магнитного поля и распространяющиеся вдоль него, являются электростатическими плазменными колебаниями.

Для волн, бегущих поперек магнитного поля, но поляризованных вдоль него, вместо (4.1.5) имеем:

(4.1.30)

Это при подстановке (5.1.27)дает дисперсионное соотношение:

(4.1.31)

такое же, как для описания распространения электромагнитных волн в плазме без магнитного поля.Так же выглядит и квадрат показателя преломления:

(4.1.32)

Эту величину можно рассматривать как продольную диэлектричес­кую проницаемость плазмы. Без магнитного поля диэлектрическая проницаемость плазмы изотропна и по любому направлению дается выражением (4.1.32).

4.1.4.Альфвеновские волны.

Рассмотрим волны, распространяющиеся вдоль магнитного поля при произвольной поляризации. Вновь разложим ее на две независимые друг от друга составляющие: с продольной и поперечной поляризацией относительно магнитного поля. Волна с продольной поляризацией (т.е. с направлением электрического поля вдоль направления распространения волны и, в данном случае, также вдоль магнитного поля) вырождается в продольные колебания на плазменной частоте, уже рассмотренные нами. Здесь нас интересует другая компонента: волна бегущая вдоль магнитного поля с поперечной поляризацией. Для такой волны

(4.1.33)

и (4.1.5) сведется к виду

(4.1.34)

Можно еще больше упростить полученное выражение, если пренебречь первым членом в правой части (4.1.34). Это будет означать, что ток, переносимый частицами велик по сравнению с током смещения, т.е. влияние плазмы на распространение волны велико (показатель преломления много больше единицы, ситуация сильно отличается от случая распространения волны в вакууме):

(4.1.35)

Тогда из (4.1.34) следует

(4.1.36)

Отсюда видно, что ток направлен по электрическому полю, которое перпендикулярно к магнитному. Поэтому уравнение (4.1.18) преобразуется к следующему виду:

(4.1.37)

Подставив в (4.1.37) электрическое поле, даваемое (4.1.36), получим

(4.1.38)

Исследуем дисперсионное уравнение (4.1.38) в области низких частот.Если

(4.1.39)

оно существенно упростится:

(4.1.39)

При этом показатель преломления и фазовая скорость волны выразятся соотношениями:

(4.1.40)

(4.1.41)

где - массовая плотность плазмы. - альфвеновская скорость. Сами волны этого типа называются альфвеновскими. Они могут быть наглядно интерпретированы как поперечные колебания вмороженных в плазму силовых линий магнитного поля вместе с плазмой. Скорость их распространения постоянна (дисперсии нет)

4.1.5. Дисперсия вблизи циклотронных частот.

Если (4.1.39) не выполнено, то возникает дисперсия и проявляются гиротропные свойства плазмы. Распишем (4.1.38) в проекциях, имея в виду, что :

(4.1.42)

(4.1.43)

Дисперсионное уравнение получается приравниванием нулю определителя этой системы, что проще сделать, выразив отношение амплитуд:

(4.1.44)

откуда

(4.1.45)

или

(4.1.46)

Знаменатель обращается в нуль при двух резонансных частотах (или частотах аномальной дисперсии). Если не пренебрегать при выводе m_e по сравнению с M, то эти частоты в точности равны . Из (4.1.46) получаются значения очень близкие к ним (с точностью до величин порядка опущенных при выводе (4.1.12) ).

Из (4.1.44) следует

т.е. (4.1.47)

Амплитуда тока одинакова во всех направлениях , что из-за (4.1.36) относится и к амплитуде . В течение цикла, меняется лишь фаза волны, т.е. она вращается вокруг направления . Такие волны называются волнами с круговой поляризацией. Два знака в (4.1.46) соот­ветствуют вращению в противоположных направлениях.

Одна из них может существовать лишь при - это обыкновенная волна. Вторая лишь при - необыкновенная. У первой вращается в сторону вращения ионов в магнитном поле, у второй - в сторону электронного вращения.

4.1.6. Магнитный звук.

Рассмотрим теперь волны, распространяющиеся перпендикулярно маг­нитному полю. В этом случае, как и ранее, волна, поляризованная вдоль отщепляется (это электромагнитная волна) и достаточно рас­смотреть волны с плоскостью поляризации . Пусть ось х - вдоль направления распространения , z - вдоль , y^ к этим направлениям. Тогда составляющие уравнения (4.1.5) по х и y примут вид:

(4.1.48)

(4.1.49)

Выразив отсюда E_x и E_y и подставив в (4.1.18) получим

(4.1.50)

(4.1.51)

Здесь амплитуды E_x и E_y, j_x и j_y не одинаковы, т.е. волна имеет эллиптическую поляризацию. Дисперсионное соотношение получаем, приравнивая нулю определитель системы (4.1.50) - (4.1.51) .

Вновь рассмотрим предельную область очень низких частот.

(4.1.52)

Пусть также N>>1, т.е. скорость распространения волны мала по сравнению со скоростью света (сильно влияние плазмы, можно пренебречь токами смещения),:

(4.1.53)

В этом случае из (4.1.50) следует

(4.1.54)

и из системы (4.1.48) - (4.1.49)

(4.1.55)

т.е. в этой области эллиптическая волна вырождается в линейно поляризованную. Приближенное дисперсионное соотношение для этой области можно получить, рассматривая лишь (4.1.51):

(4.1.56)

С учетом (4.1.54) ясно, что коэффициент при j_y должен быть мал, т.е. дисперсионное соотношение в этой области частот стремится к

(4.1.57)

Что совпадает с (4.1.39). Это значит, что при низких частотах волны в плазме распространяются как параллельно, так и перпендикулярно магнитному полю с одной и той же скоростью - альфвеновской (см. (4.1.41)). Однако здесь другая природа волн. Там это поперечные, электромагнитные волны. Здесь процесс колебаний можно рассматривать как сжатие и расширение плазмы вместе с вмороженным в нее магнитным полем. Это похоже на распространение звука. Поэтому и называется магнитным звуком. Вместо газового давления здесь действует магнитное давление .

Если в обычную для скорости звука формулу

вместо p подставить , взяв g_м =2 для вмороженного поля, то получится

,

что совпадает с формулой (4.1.41).

4.2. Волны в горячей плазме в МГД приближении.

4.2.1.Основные уравнения.

В этой модели учитывается давление плазмы. Принимается, что электронное давление действует на электроны, ионное ‑ на ионы, а взаимодействие между этими двумя жидкостями описывается электрическим сопротивлением плазмы. Идеальная проводимость – отсутствие взаимодействия между ионами и электронами.

Уравнения движения электронов и ионов в линейном гидродинамическом приближении без взаимодействия:

(4.2.1)

(4.2.2)

Полные производные заменены частными в силу линейного приближения. Если сложить (4.2.1) и (4.2.2), то с учетом

(4.2.3)

и определения плотности тока

(4.2.4)

то получится для массовой скорости

(4.2.5)

где

– массовая скорость (4.2.6)

и

–массовая плотность (4.2.7)

если разделить (4.2.1) на , а (4.2.2) на и вычесть (4.2.1) из (4.2.2), выбросив члены с в знаменателе (т.е. считая ионы неподвижными) то получим уравнение идеальной проводимости

(4.2.8)

Для учета джоулевой диссипации в правую часть добавляют член . Тогда получается обобщенный закон Ома с учетом электронного давления

(4.2.9)

где

Неточность описания плазмы с помощью (4.2.1)– (4.2.8):

а) не учитывается анизотропия давлений – в разреженной плазме давление может быть не скаляром, а тензором. Это часто неважно.

б) не описывается бесстолкновительная диссипация. Это может привести к тому, что некоторые типы колебаний, получающееся в гидродинамическом приближении на самом деле не реализуются.

4.2.2. Скорость звука.

Чтобы описать влияние давления на волновые движения нужно связать со скоростью движения вещества.

Пренебрегая диссипативными процессами, считаем, что состояние вещества меняется по адиабатическому закону

(4.2.10)

откуда

(4.2.11)

(4.2.12)

Запишем ещё уравнение непрерывности

(5.2.13)

в линейном приближении это сведется к

(4.2.14)

– возмущенная концентрация, . Что для плоской волны вида

даст (4.2.15)

Если невозмущенная плотность – постоянна в пространстве, то

(4.2.16)

и тогда, из (4.2.12) следует

(4.2.17)

Это уравнение решается совместно с уравнением движения. Поскольку взаимодействием ионов и электронов мы пренебрегаем, уравнения(4.2.11) – (4.2.17) могут применяться отдельно к ионам и электронам, и меняются при этом независимо.

Для газа из нейтральных частиц (4.2.17) решается совместно с линеаризованным уравнением Эйлера

(4.2.18)

которое для плоской волны дает

(4.2.19)

Выразив отсюда 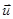, подставим его в (4.2.17) и, для продольных волн получим дисперсионное уравнение

(4.2.20)

Здесь – обычная скорость звука. По аналогии удобно ввести ионную и электронную скорости звука

(4.2.21)

(4.2.22)

где и – температуры ионов и электронов в энергетических единицах.

Тогда (4.2.12) для i и e можно записать

(4.2.23)

(5.2.24)

а (4.2.17) в виде

(4.2.25)

(4.2.26)

Пусть в плазме могут распространяться обычные звуковые волны, для которых можно пренебречь разделением зарядов и эл. токами. Это значит, что электроны и ионы должны иметь одинаковые средние (упорядоченные) скорости

(4.2.27)

Тогда сложение (4.2.25) и (4.2.26) дает (с учетом ) для общего давления

(4.2.28)

Это можно записать в виде аналогичном (4.2.25)

(4.2.29)

если определить скорость звука соотношением

(4.2.30)

Это – так называемая скорость ионного звука. Она определяется суммарной и массой ионов.

4.2.3.Плазменные волны и ионный звук.

Рассмотрим вначале продольные волны без магнитного поля. У этих волн т.е.

Уравнения движения (4.2.1) и (4.2.2) для продольных волн без магнитного поля с учетом (4.2.25) и (4.2.26) принимают вид

(4.2.31)

(4.2.32)

Отсюда видно, что в данном случае и . Эти уравнения решаются совместно с уравнением

(4.2.33)

где

(4.2.34)

В (4.2.34) входят только возмущения концентраций, т.к. невозмущенное . Отсюда для продольных волн

(4.2.35)

Этот результат – закон сохранения электрического заряда

(4.2.36)

Подстановка (4.2.35) в (4.2.36) дает для продольной плоской волны

(4.2.37)

или с учетом квазинейтральности (4.2.3)

(4.2.38)

подстановка (4.2.38) в (4.2.31) и (4.2.32) дает

(4.2.39)

(4.2.40)

определитель этой системы дает дисперсионное соотношение для продольных волн в плазме без магнитного поля

(4.2.41)

Здесь 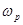– электронная плазменная частота.

Заметим, что

(4.2.42)

Расположим уравнение (4.2.41) по степеням частоты

(4.2.43)

Это уравнение определяет две различные ветви колебаний. Высокочастотная или электронная ветвь получается если пренебречь свободным членом. Тогда

(4.2.44)

Практически , поэтому

(4.2.44 а)

В (4.2.44 а) входят величины, относящиеся только к электронам. Поэтому это – электронная ветвь.

Ионная ветвь получается, если пренебречь . Тогда дисперсионное соотношение

(4.2.45)

Для длинных волн (4.2.45) стремится к

(4.2.46)

Это отвечает скорости распространения ионного звука.

Для коротких волн

(4.2.47)

т.к.

4.3. Кинетический подход в изучении волн в плазме.

4.3.1. Дисперсионное уравнение в кинетике в отсутствии магнитного поля.

Рассмотрим принцип получения дисперсионного уравнения в кинетике на наиболее

простом примере продольных высокочастотных колебаний без внешнего магнитного поля. Считая, что частоты интересующих нас колебаний очень высоки, , и ионная компонента плазмы в них не участвует, можем ограничиться только кинетическим уравнением для электронов:

(4.3.1)

В линейном приближении: , — равновесная по отношению к рассматриваемому процессу. Пусть —однородна и постоянна во времени, тогда из (4.3.1):

(4.3.2)

—внешнее магнитное поле; —собственное поле волны. Рассматриваем плоскую волну:

происходит только от вихревого электрического поля, так как: . В плоской продольной волне электрическое поле безвихревое (потенциальное). зависит только от x. Поэтому и уравнение (4.3.2) сводится к :

(4.3.3)

Электрическое поле находим из:

(4.3.4)

(так как , то не вносит вклад в плотность заряда—реально это означает квазинейтральность плазмы в равновесном состоянии). Чтобы получить дисперсионное соотношение нужно из (4.3.3) выразить через и подставить в (4.3.4):

(4.3.5)

подставив это в (4.3.4), получим:

(4.3.6)

Это и есть дисперсионное уравнение. Удобнее ввести нормированную функцию распределения 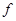, определенную следующим образом:

, то есть (4.3.7)

где —полная концентрация электронов.

Условие на 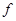тогда:

(4.3.8)

При этом (4.3.6) перепишется:

(4.3.9)

Имея в виду, что при , преобразуем интеграл, беря его по частям:

.

Получим дисперсионное соотношение в виде:

(4.3.10)

иногда это удобнее.

Если —холодная плазма, неподвижная, то из (4.3.10) имеем:

—электронные ленгмюровские колебания.

Интеграл в (4.3.9) можно вычислить, заменив в знаменателе на , где —бесконечно малое положительное число.

(4.3.10а)

используя соотношение:

(4.3.11)

диэлектрическую проницаемость можно представить в виде:

(4.3.12)

где

(4.3.13)

(4.3.14)

где —главное значение интеграла. Отсюда следует, что —комплексна, если при отлична от 0. При комплексном комплексна и частота собственных колебаний плазмы. Мнимую часть частоты собственных колебаний легко найти, когда она мала по сравнению с вещественной, что возможно при малом . Действительно, при мнимую добавку к частоте достаточно учесть только в функции .

Разлагая ее по степеням :

(4.3.15)

откуда следует выражение для действительной и мнимой части частоты колебаний:

(4.3.16)

(4.3.17)

здесь ;

4.3.2. Диэлектрическая проницаемость максвелловской плазмы

Рассмотрим случай максвелловской функции распределения частиц

плазмы по скоростям:

(4.3.18)

Подставив (4.3.18) в выражения для действительной и мнимой частей диэлектрической проницаемости, полученные в предыдущем параграфе (4.3.13) и (4.3.14), получим:

(4.3.19)

(4.3.20)

Здесь - тепловая скорость, - дебаевский радиус. Эти выражения получены для вещественных w . Их аналитическое продолжение на область комплексных w сводится к простой замене вещественных w на комплексные. Объединяя их, находим, что при любом комплексном w диэлектрическая проницаемость максвелловсой плазмы имеет вид:

(4.3.21)

где ;

W(X) – интеграл вероятности от комплексного аргумента, называемый также функцией Крампа. Эту функцию можно аппроксимировать следующими приближенными выражениями, удобными при аналитическом подходе к исследованию дисперсионных уравнений:

При

; (4.3.22)

При

(4.3.23)

При наличии многокомпонентной плазмы в выражении (4.3.21) для следует в «плазменном слагаемом» учесть сумму по компонентам:

(4.3.24)

a - сорт частиц (электроны, ионы)

4.3.3. Бесстолкновительное затухание плазменных волн (затухание Ландау).

Будем исходить из общего выражения для диэлектрической проницаемости для плазмы с максвелловским распределением электронов по скоростям

где , , .

Приближение холодной плазмы получится при , . Воспользуемся выписанным ранее разложением W(x) для случая , удержав первые три члена в мнимой части