Результаты работы и их анализ

Томск 2002

Введение

Целью данной работы является изучение зависимости энергетической светимости нагретого тела от его температуры.

Описание эксперементальной установки

Измерения проводятся на установке, принципиальная схема которой изображена на рис. 1.1.

Излучающим телом является платиновая нить длиной l=7 см и диаметром d=0.2 мм, заключённая в стеклянный откаченный баллон. Нагрев нити осуществляется постоянным электрическим током. Для этого переменное напряжение, регулируемое при помощи лабораторного автотрансформатора (ЛАТР), подаётся на вход выпрямителя, к выходу которого подключена платиновая нить. Вольтметр и миллиампер метр показывают, соответственно, падение напряжения и ток в цепи накала нити. В непосредственном контакте с нитью находится хромель-копелевая термопара. В её цепь включен милливольтметр, который позволяет измерять величину термо-ЭДС (ТЭДС), возникающую при нагреве спая термопары.

Рис. 1.1 – Схема экспериментальной установки.

Методика измерений и обработки результатов

Измерение потока излучения Ф в платиновой нити заменяется измерением подводимой к ней электрической мощности Р, энергетическая светимость R вычисляется как отношение этой мощности к площади цилиндрической поверхности платиновой нити S - формула (3.1).

Температура нити вычисляется исходя из показаний милливольтметра, измеряющего ТЭДС термопары, по формуле (3.2).

Получив экспериментальным путём зависимость R(T) определяем коэффициент серости платиновой нити a и показатель степени z при температуре, для чего логарифмируем выражение (3.3) и получим выражение (3.4).

Не трудно заметить что, приняв x=lnT и y= lnR(T) можно построить линеаризованный график в осях x,y, в котором угловой коэффициент прямой будет равен z, а свободный член - ln(as).

Но для нахождения углового коэффициента, свободного члена, а так же их погрешностей целесообразней использовать метод наименьших квадратов – формулы (3.5) – (3.8). Значение a найдём по формуле (3.9), а её погрешность по формуле (3.10).

Основныерасчётные формулы

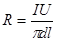(3.1)

где R – энергетическая светимость;

I – ток в нити;

U – напряжение нити;

d – диаметр нити;

l – длина нити.

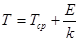(3.2)

где T – температура нити;

T_ср – температура окружающей среды;

E – ТЭДС;

k – коэффициент пропорциональности (0,064 мВ/К).

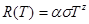(3.3)

где a - коэффициент серости;

s – постоянная Стефана-Больцмана (5,7·10^-8 Вт/(м²К⁴));

z – искомый показатель степени.

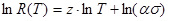(3.4)

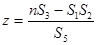(3.5)

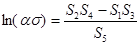(3.6)

где ; ; ; ; ;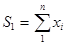

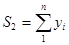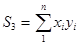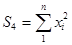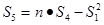n – количество опытов;

x - lnT;

y – lnR;

i – номер опыта.

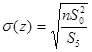(3.7)

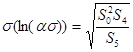(3.8)

где ; .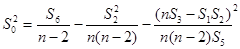

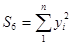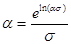(3.9)

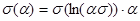(3.10)

где ln(as) – логарифм найденный по формуле (3.6).

результаты работы и их анализ

Результаты прямых и косвенных измерений приведены в таблице 4.1.

Таблица 4.1 - Результаты прямых и косвенных измерений

№	U, В	I, А	UI/S, ВА/м2	ln(UI/S)	ТЭДС, мВ	T, К	ln(T)
	0,15	0,137	467,2	6,15	17,0		6,33
	0,20	0,162	736,7	6,60	22,5		6,47
	0,25	0,185	1051,6	6,96	27,7		6,59
	0,30	0,206	1405,1	7,25	32,5		6,69
	0,35	0,225	1790,5	7,49	36,2		6,76
	0,40	0,250	2273,6	7,73	39,0		6,80
	0,45	0,268	2742,0	7,98	42,5		6,86

По данным таблицы построим линеаризованный график зависимости ln(UI/S) от lnT – рис. 4.1.

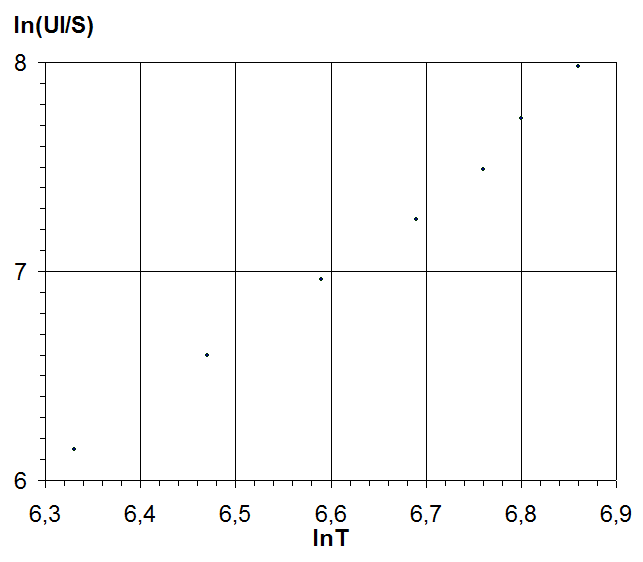
Рис. 4.1 - Линеаризованный график зависимости ln(UI/S) от lnT.

По формуле (3.5) найдём значение показателя z, по формуле (3.7) абсолютную погрешность этого значения.

z=3.3;

s(z)=0.8.

По формуле (3.6) найдём значение свободного члена ln(as), по формуле (3.8) абсолютную погрешность этого значения.

ln(as)=-14.8;

s(ln(as))=5.5.

По формуле (3.9) найдём значение коэффициента серости a, по формуле (3.10) абсолютную погрешность этого значения.

a=6.8;

s(a)=37.

заключение

В ходе проведённой лабораторной работы мы экспериментально подтвердили закон Стефана-Больцмана, в частности определили показатель степени при температуре z, который совпал с основным значением в пределах погрешности. Однако мы не можем сказать ничего определённого о коэффициенте серости a, так как он, во первых, намного превышает единицу, что нереально, во вторых, погрешность коэффициента серости намного превышает сам коэффициент серости.