Количественно-качественное сравнение теорий Ньютона и Пуассона

Произведем сравнение результатов, полученных путем применения формул (28) и (28а) – уравнений Ньютона и Пуассона.

Подсчитаем для воздуха:

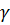=1,4; ρ = 1,29 при комнатной температуре (20° С, Т =293 К) формула Ньютона дает u =290 м/сек, формула Пуассона u=331 м/сек. Формула Пуассона хорошо подтверждается на опыте и для других газов (но крайней мере при не очень высоких частотах):

1)для гелия

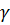=1,7; ρ =0,179 при температуре 0°C, Т=273 К, давление 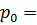101 325 Па

формула Ньютона: u = 752 м/сек

формула Пуассона: u=980 м/сек

2)для аммиака

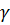=1,3; ρ =0,77 при температуре 0°C, Т=273 К, давление 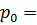101 325 Па

формула Ньютона: u = 362 м/сек

формула Пуассона: u=413 м/сек

3)для углекислого газа

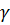=1,2; ρ =1,98 при температуре 0°C, Т=273 К, давление 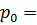101 325 Па

формула Ньютона: u = 226 м/сек

формула Пуассона: u=250 м/сек

Этим оправдывается предположение о том, что сжатие и разрежение газа в звуковой волне являются практически адиабатическими процессами.

Как видно из результатов, полученные значения скорости звука из разных формул в одном случае небольшая (для углекислого газа всего 24 м/с), а в другом случае довольно значительная (для гелия она составляет 228 м/с).

Это происходит потому, что количество степеней свободы этих газов различно.

Так как 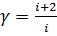, где i-количество степеней свободы молекул газа

Для одноатомного идеального газа (гелий) i=3, т.е.

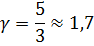
Отсюда и большая разница в расчетах при использовании двух разных формул, чем, например, для кислорода двухатомного газа (i=5):

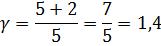
То есть квадратный корень из 1,7 будет больше, чем из 1,4. Соответственно, чем большим количеством степеней свободы обладает газ, тем меньше разница, полученная при расчетах по разным формулам.

Вывод

1) Исследовано распространение упругих волн в средах;

2)В ходе работы было выяснено, что теплопроводность газов и жидкостей очень мала, поэтому можно считать в первом приближении, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит адиабатически, т. е. без заметного теплообмена с соседними частями;

3)Произведена количественно-качественное сравнение теорий Ньютона и Пуассона о распространении упругих волн в среде. Сравнение теоретических расчетов и экспериментальных данных показало, что теория Пуассона о том, что распространение упругих волн происходит адиабатно, лучше описывает реальные условия, чем теория Ньютона.

Эта разница тем больше заметна, чем меньше степеней свободы у рассматриваемого газа. Чем сложнее газ, тем меньшую разницу дают расчеты по формулам Ньютона и Пуассона.

Список литературы

1. Горелик, Г. С. Колебания и волны. Введение в акустику, радиофизику и оптику/ Г.С. Горелик. – 2-е издание. – Москва. – 1959.

2. Савельев, И. В. Курс общей физики, том I. Механика, колебания и волны, молекулярная физика/И.В. Савельев. – Москва: Наука. – 1970.

3. Стрелков, С.П. Введение в теорию колебаний/С.П. Стрелков. 2-е издание. – Москва: Наука. – 1964.

4. Кикоин, И.К. Таблицы физических величин. Справочник/ И.К. Кикоин.- Москва: Атомиздат.