Как полетели на Луну герои Уэллса

Интересно описан у романиста самый момент отправления межпланетного вагона в путь. Тонкий слой «кеворита», покрывающий наружную поверхность снаряда, делает его как бы совершенно невесомым. Вы понимаете, что невесомое тело не может лежать спокойно на дне воздушного океана; с ним должно произойти то же, что произошло бы с пробкой, погруженной на дно озера: пробка быстро всплыла бы на поверхность воды. Точно так же невесомый снаряд, – отбрасываемый к тому же и инерцией вращения земного шара, – должен стремительно взлететь ввысь и, дойдя до крайних границ атмосферы, свободно продолжать свой путь в мировом пространстве. Герои романа так и полетели. А очутившись в мировом пространстве, они, открывая одни заслонки, закрывая другие, подвергая внутренность снаряда притяжению то Солнца, то Земли, то Луны, добрались до поверхности нашего спутника. Впоследствии один из путешественников в том же снаряде возвратился на Землю.

Не будем останавливаться здесь на разборе идеи Уэллса по существу, – это сделано мною в другом месте[20], где я и выяснил ее несостоятельность. Поверим на минуту остроумному романисту и последуем за его героями на Луну.

Полчаса на Луне

Посмотрим, как чувствовали себя герои повести Уэллса, очутившись в мире, где сила тяжести слабее, меньше, чем на Земле.

Вот эти любопытные страницы[21]романа «Первые люди на Луне». Рассказ ведется от лица одного из жителей Земли, только что прибывших на Луну.

«Я принялся вывинчивать крышку снаряда. Став на колени, я высунулся из люка; внизу, на расстоянии трех футов от моей головы, лежал девственный снег Луны.

Закутавшись в одеяло, Кевор сел на край люка и стал осторожно свешивать ноги. Спустив их до высоты полуфута над почвой, он после минутного колебания соскользнул вниз на почву лунного мира.

Я следил за ним через стеклянную оболочку шара. Пройдя несколько шагов, он постоял минуту, озираясь кругом, затем решился и – прыгнул вперед.

Стекло искажало его движения, но мне казалось, что это и в действительности был чересчур большой прыжок. Кевор сразу очутился от меня в расстоянии 6–10 метров. Стоя на скале, он делал мне какие‑то знаки; возможно, что он и кричал, – однако звуки но достигали меня… Но как он проделал свой прыжок?

Озадаченный, я пролез через люк и тоже спустился вниз, очутившись на краю сложной выемки. Сделав шаг вперед, я прыгнул.

Я почувствовал, что лечу, и вскоре очутился близ скалы, на которой стоял поджидавший меня Кевор; ухватившись за нее, я повис в страшном изумлении.

Кевор, нагнувшись, кричал мне визгливым голосом, чтобы я был осторожнее. Я и забыл, что на Луне напряжение тяжести в шесть раз слабее, нежели на Земле. Действительность сама напоминала мне об этом.

Осторожно, сдерживая свои движения, я поднялся на вершину скалы и, ступая словно больной ревматизмом, стал на солнце рядом с Кевором. Снаряд наш лежал на тающем сугробе снега, футах в тридцати от нас,

– Посмотрите, – обратился я, поворачиваясь к Кевору.

Но Кевор исчез.

Одно мгновение я стоял, пораженный этой неожиданностью, затем, желая заглянуть за край скалы, поспешно шагнул вперед, совершенно забыв, что я на Луне. Усилие, которое я сделал, подвинуло бы меня на один метр, будь я на Земле; на Луне же оно подвинуло меня на 6 метров, и я очутился в 5 метрах за краем скалы.

Я испытывал то ощущение витания в пространстве, которое приходится переживать во сне, когда снится, будто падаешь в бездну. На Земле человек, падая, опускается в течение первой секунды на 5 метров, на Луне же он проходит при падении в первую секунду 80 сантиметров. Вот почему я плавно порхнул вниз на глубину метров девяти. Падение показалось мне продолжительным; оно длилось секунды три. Я поплыл в воздухе и опустился плавно, как пушинка, увязши по колено в снежном сугробе на дне скалистой долины.

– Кевор! – крикнул я, осматриваясь кругом. Но нигде не было и следов его.

– Кевор! – крикнул я громче.

И вдруг я увидел его; он смеялся и делал мне знаки, стоя на голом утесе, метрах в двадцати от меня. Я не мог слышать слов, но понял смысл его жестов: он приглашал меня прыгнуть к нему.

Я колебался: расстояние казалось мне слишком огромным.

Но скоро я сообразил, что раз Кевор проделал такой прыжок, то, наверное, удастся прыгнуть и мне.

Отступив на шаг, я прыгнул изо всех сил. Стрелой взвился я в воздух и, казалось, никогда не опущусь вниз. Это был фантастический полет – чудовищный, как в сновидении, но в то же время восхитительно приятный.

Прыжок оказался слишком сильным: я перелетел над головой Кевора».

Стрельба на Луне

Следующий эпизод, взятый из повести выдающегося советского изобретателя К. Э. Циолковского «На Луне», поможет нам уяснить условия движения под действием силы тяжести. На Земле атмосфера, препятствуя движению в ней тел, заслоняет от нас простые законы падения, усложняя их добавочными условиями. На Луне воздух отсутствует совершенно. Луна была бы превосходной лабораторией для изучения падения тел, если бы мы могли на ней очутиться и заниматься там научными исследованиями.

Обращаясь к эпизоду повести, поясним, что два собеседника приводимого далее отрывка находятся на Луне и желают исследовать, как будут двигаться там пули, вылетевшие из ружья.

«– Но будет ли тут работать порох?

– Взрывчатые вещества в пустоте должны проявлять себя даже с большей силой, чем в воздухе, так как последний только препятствует их расширению; что же касается кислорода, то они в нем но нуждаются, потому что все необходимое его количество заключается в них самих.

– Установим ружье вертикально, чтобы пулю после взрыва отыскать поблизости…

Огонь, слабый звук[22], легкое сотрясение почвы.

– Где же пыж? Он должен быть тут, поблизости.

– Пыж улетел вместе с пулей и едва ли от нее отстанет, так как только атмосфера мешает ему на Земле поспевать за свинцом; здесь же пух падает и летит вверх с такой же стремительностью, как и камень. Возьми пушинку, торчащую из подушки, а я возьму чугунный шарик. Ты можешь кидать свою пушинку и попадать ею в цель, даже отдаленную, с таким же удобством, как я шариком. Я могу, при малой тяжести, кинуть шарик метров на 400; ты на такое же расстояние можешь бросить пушинку; правда, ты никого ею не убьешь и при бросании даже не почувствуешь, что ты что‑нибудь бросаешь. Бросим наши метательные снаряды изо всех сил, – которые у нас не очень различны, – и в одну цель: вон в тот красный гранит…

Пушинка опередила немного чугунный шарик, как бы увлекаемая сильным вихрем.

– Но что это? Со времени выстрела прошло три минуты, а пули нет?

– Подожди две минуты, и она, наверное, вернется. Действительно, через указанный срок мы ощущаем легкое сотрясение почвы и видим прыгающий невдалеке пыж.

– Как долго летала пуля! На какую же высоту она должна подняться?

– Километров на семьдесят. Эту высоту создают малая тяжесть и отсутствие воздушного сопротивления».

Проверим. Если для скорости пули в момент вылета из ружейного ствола взять сравнительно скромную цифру 500 м в секунду (для современных ружей это раза в полтора меньше действительной), то высота поднятия на Земле, при отсутствии атмосферы, была бы:

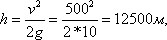
т. е. 12,5 км. На Луне же, где напряжение тяжести в 6 раз слабее, вместо g надо взять 10/6 м/сек²; достигаемая пулей высота должна равняться:

12 500 × 6 = 75 км.

В бездонном колодце

О том, что делается в глубоких недрах нашей планеты, известно пока очень мало. Одни полагают, что под твердой корой в сотню километров толщины начинается огненно‑жидкая масса; другие считают весь земной шар отвердевшим до самого центра. Решить вопрос трудно: ведь самая глубокая скважина простирается не глубже 7,5 км, самая глубокая шахта, в которую проник человек, расположена на глубине 3300 м[23], а радиус земного шара равен 6400 км. Если бы можно было просверлить через нашу планету сквозной колодец, прорезающий земной шар по диаметру, – тогда подобные вопросы были бы разрешены. Современная техника далека еще от возможности осуществления подобных предприятий, – хотя все прорытые в земной коре буровые скважины, взятые вместе, составили бы длину, превышающую диаметр нашей планеты. О прорытии сквозного туннеля через земной шар мечтали в восемнадцатом веке математик Мопертюи и философ Вольтер. К этому проекту, правда, в ином, более скромном масштабе, вернулся французский астроном Фламмарион; мы воспроизводим здесь заглавный Рисунок его статьи, посвященной этой теме (рис. 44).

Ничего подобного, конечно, пока еще не сделано; но воспользуемся воображаемым бездонным колодцем, чтобы заняться одной любопытной задачей. Как вы думаете, что было бы с вами, если бы вы упали в такой бездонный колодец (о сопротивлении воздуха на время забудем)? Разбиться о дно вы не можете, дна здесь не существует, – но где же вы остановитесь? В центре Земли? Нет.

Рисунок 44. Если просверлить земной шар по диаметру…

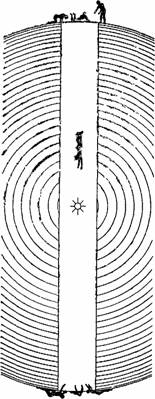
Рисунок 45. Упав в колодец, прорытый через центр земного шара, тело будет качаться безостановочно от одного конца колодца до другого, совершая каждое полное качание в течение 1 часа 24 минут.

Когда вы долетите до центра, тело ваше будет иметь такую колоссальную скорость (около 8 км/сек), что об остановке в этой точке не может быть и речи. Вы промчитесь далее и будете нестись, постепенно замедляя движение, пока не поравняетесь с краями противоположного конца колодца. Здесь надо будет вам покрепче ухватиться за края, – иначе вы вновь проделаете прогулку через весь колодец до другого конца. Если и тут не удастся вам ухватиться за что‑нибудь, вы опять полетите в колодец и будете качаться так без конца. Механика учит, что при таких условиях (если только, повторяю, пренебречь сопротивлением воздуха в колодце) тело должно качаться туда и назад вечно[24].

Какова была бы продолжительность одного такого качания? Оказывается, что весь путь туда и обратно занял бы 84 минуты 24 секунды, т. е. круглым счетом полтора часа.

«Так было бы, – продолжает Фламмарион, – если бы колодец вырыт был по оси от полюса до полюса. Но достаточно перенести точку отправления на какую‑либо иную широту – на материк Европы, Азии или Африки, – и придется принять в расчет влияние вращения Земли. Известно, что каждая точка земной поверхности пробегает на экваторе 465 м в секунду, а на широте Парижа – 300 м. Так как окружная скорость возрастает с удалением от оси вращения, то свинцовый шарик, например, брошенный в колодец, падает не по вертикали, а уклоняется несколько к востоку. Если вырыть бездонный колодец на экваторе, то ширина его должна быть весьма значительна, либо же он должен быть сильно скошен, потому что тело, падающее с поверхности Земли, пронеслось бы далеко к востоку от ее центра.

Если бы входное отверстие колодца находилось на одном из плоскогорий Южной Америки, на высоте, положим, двух километров, а противоположный конец туннеля приходился бы на уровне океана, то человек, который по неосторожности свалился бы в американское отверстие, достиг бы противоположного конца с такой скоростью, что вылетел бы из него на высоту двух километров.

А если бы оба конца колодца приходились на уровне океана, можно было бы подать летящему человеку руку в момент появления его у отверстия, когда скорость полета равняется нулю. В предыдущем же случае следовало бы, напротив, с опаскою посторониться от чересчур стремительного путешественника».

Сказочная дорога

В свое время в С.‑Петербурге появилась брошюра со странным заглавием: «Самокатная подземная железная дорога между С.‑Петербургом и Москвой. Фантастический роман пока в трех главах, да и то неоконченных». Автор этой брошюры, А. А. Родных, предлагает остроумный проект, с которым интересно познакомиться любителю физических парадоксов.

Проект состоит «в проведении 600‑километрового туннеля, который должен соединить обе наши столицы по совершенно прямой подземной линии. Таким образом, впервые явилась бы возможность для человечества совершать путь по прямой, а не ходить кривыми путями, как это было до сих пор». (Автор хочет сказать, что все наши дороги, подчиняясь кривизне земной поверхности, следуют по дугам, между тем как проектируемый туннель пройдет по прямой линии – по хорде.)

Такой туннель, если бы его можно было прорыть, имел бы удивительное свойство, каким не обладает ни одна дорога в мире. Оно заключается в том, что любой экипаж в подобном туннеле должен двигаться сам собой. Вспомним наш подземный колодец, пробуравливающий земной шар. Ленинградо‑московский туннель – тот же колодец, только просверленный не по диаметру, а по хорде. Правда, при взгляде на рис. 46 может казаться, что туннель прорыт горизонтально и что поезду, следовательно, нет причины катиться по нему в силу тяжести. Но это лишь обман зрения: проведите мысленно радиусы к концам туннеля (направление радиуса есть направление отвеса); вы поймете тогда, что туннель прорыт не под прямым углом к отвесу, т. е. не горизонтально, а наклонно.

Рисунок 46. Если бы прорыть туннель между Ленинградом и Москвой, то поезда мчались бы в нем туда и обратно под собственным весом, без паровозов.

В таком косом колодце всякое тело должно качаться, увлекаемое силою тяжести, вперед и назад, все время прижимаясь ко дну. Если в туннеле устроить рельсы, то железнодорожный вагон будет сам катиться по ним: вес заменит тягу паровоза. Вначале поезд будет двигаться очень медленно. С каждой секундой скорость самокатного поезда будет возрастать; вскоре она дойдет до невообразимой величины, так что воздух в туннеле будет уже заметно мешать его движению. Но забудем на время об этом досадном препятствии, мешающем осуществлению многих заманчивых проектов, и проследим за поездом дальше. Домчавшись до середины туннеля, поезд будет обладать такой огромной скоростью, – во много раз быстрее пушечного снаряда! – что с разбега докатится почти до противоположного конца туннеля. Если бы не трение, не было бы и этого «почти»: поезд без паровоза сам доехал бы из Ленинграда в Москву. Продолжительность перелета в один конец, как показывает расчет, – та же, что и для падения сквозь туннель, прорытый по диаметру: 42 минуты 12 секунд. Странным образом она не зависит от длины туннеля; путешествия в туннеле Москва – Ленинград, Москва – Владивосток или Москва – Мельбурн продолжались бы одинаковое время[25].

То же повторялось бы с любым другим экипажем: дрезиной, каретой, автомобилем и т. д. Поистине сказочная дорога, которая, сама оставаясь неподвижной, мчит по себе все экипажи от одного конца до другого, и притом с невообразимой быстротой!

(Интересующиеся математической стороной этой задачи могут найти подробный разбор ее в моей статье, напечатанной в журнале «Математика и физика в школе», 1936, № 3, стр. 106–107.)

Как роют туннели?

Взгляните на рис. 47, изображающий три способа проведения туннелей, и скажите, какой из них прорыт горизонтально?

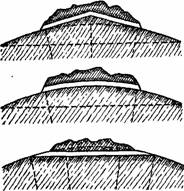
Рисунок 47. Три способа прокладывать туннели сквозь горы.

Не верхний и не нижний, а средний, идущий по дуге, которая во всех точках образует прямые углы с направлением отвесных линий (или земных радиусов). Это и есть горизонтальный туннель, – его изгиб вполне соответствует кривизне земной поверхности.

Большие туннели прорывают обыкновенно так, как показано вверху: по прямым линиям, касательным к земной поверхности в крайних точках туннеля. Такой туннель сначала идет немного вверх, затем вниз. Он представляет то удобство, что вода не застаивается в нем, а сама стекает к краям.

Если бы туннель рылся строго горизонтально, то длинный туннель имел бы дугообразную форму. Вода не имела бы стремления вытекать из него, так как в каждой его точке находилась бы в равновесии. Когда такой туннель длиннее 15 км (Симплонский, например, имеет в длину 20 км), то, стоя у одного выхода, нельзя видеть другого: луч зрения упирается в потолок, так как средняя точка такого туннеля более чем на 4 м возвышается над его конечными точками.

Наконец, если прорыть туннель по прямой линии, соединяющей крайние точки, он будет с обоих концов иметь легкий наклон вниз к середине. Вода не только не будет вытекать из него, но, напротив, скопится в средней, самой низкой его части. Зато, стоя у одного конца такого туннеля, можно будет видеть другой. Прилагаемые рисунки поясняют сказанное[26].

Глава пятая