Формула Вейцзеккера для энергии связи ядра
С капельной моделью ядра связана полуэмпирическая формула Вейцзеккера для энергии связи ядра.
В первом приближении можно считать, что энергия связи ядра 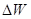 пропорциональна массовому числу А (2.3) (мы исключаем из рассмотрения самые легкие ядра):
пропорциональна массовому числу А (2.3) (мы исключаем из рассмотрения самые легкие ядра):
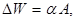 (3.1)
(3.1)
В данном случае предполагается, что все нуклоны в ядре являются равноправными. Далее следует учесть, что нуклоны, которые находятся на поверхности ядра, притягиваются только с внутренней стороны ядра, а не со всех сторон, что имеет место для нуклонов в центре ядра. В связи с этим энергия связи ядра уменьшается на величину пропорциональную поверхности ядра. Поскольку 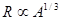 , то энергия связи уменьшается на величину пропорциональную
, то энергия связи уменьшается на величину пропорциональную  . С учетом этого и (3.1) получаем:
. С учетом этого и (3.1) получаем:
 (3.2)
(3.2)
где 
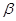 - коэффициент пропорциональности.
- коэффициент пропорциональности.
Следующая поправка к энергии связи ядра связана с кулоновским расталкиванием протонов в ядре. Кулоновская энергия равномерно заряженной ядерной капли пропорциональна  и обратно пропорциональна радиусу капли
и обратно пропорциональна радиусу капли 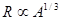 . Кулоновское отталкивание уменьшает энергию связи (3.2):
. Кулоновское отталкивание уменьшает энергию связи (3.2):
 , (3.3)
, (3.3)
где  - коэффициент пропорциональности.
- коэффициент пропорциональности.
Формула (3.3) для энергии связи ядра объяснена в рамках капельной модели. Последующие поправки уже нельзя объяснить в рамках этой модели. Первая такая поправка связана с симметрией в строении атомных ядер. Для легких ядер число протонов примерно равно числу нейтронов. Это приводит к тому, что ядра, у которых 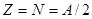 , обладают наибольшей устойчивостью. Отклонение от данного равенства в ту или иную сторону приводит к уменьшению энергии связи. Нарушение равенства между протонами и нейтронами, в пользу последних, наблюдается для тяжелых ядер и обусловлено кулоновским расталкиванием протонов, которое учтено предыдущей поправкой. Следовательно, поправка, связанная с симметрией в строении ядра, может проводиться одинаковым образом для легких и тяжелых ядер. Эта поправка должна зависеть от разности
, обладают наибольшей устойчивостью. Отклонение от данного равенства в ту или иную сторону приводит к уменьшению энергии связи. Нарушение равенства между протонами и нейтронами, в пользу последних, наблюдается для тяжелых ядер и обусловлено кулоновским расталкиванием протонов, которое учтено предыдущей поправкой. Следовательно, поправка, связанная с симметрией в строении ядра, может проводиться одинаковым образом для легких и тяжелых ядер. Эта поправка должна зависеть от разности  и быть симметричной по числам
и быть симметричной по числам  и
и 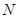 . Такой поправкой может являться
. Такой поправкой может являться 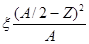 . Данная поправка наилучшим образом соответствует эксперименту. С учетом этого энергия связи ядра
. Данная поправка наилучшим образом соответствует эксперименту. С учетом этого энергия связи ядра
 , (3.4)
, (3.4)
где  - коэффициент пропорциональности. Коэффициенты пропорциональности в формуле (3.4) находятся путем сопоставления с измеренными энергиями связи.
- коэффициент пропорциональности. Коэффициенты пропорциональности в формуле (3.4) находятся путем сопоставления с измеренными энергиями связи.
Как показывают измерения, энергия связи меняется скачкообразным образом при переходе от одного ядра к другому с соседними значениями  и
и  . Формула (3.4) не учитывает такой характер изменения энергии и дает для четно-четных ядер заниженное значение энергии связи, а для нечетно-нечетных завышенное. Для правильного описания энергии связи ядра вводят в формулу (3.4) еще одну поправку
. Формула (3.4) не учитывает такой характер изменения энергии и дает для четно-четных ядер заниженное значение энергии связи, а для нечетно-нечетных завышенное. Для правильного описания энергии связи ядра вводят в формулу (3.4) еще одну поправку  , где
, где
 .
.
С учетом данной поправки формула для энергии связи ядра приобретает вид:
 . (3.5)
. (3.5)
Коэффициенты пропорциональности, подобранные по экспериментальным данным, имеют значения:
 .
.
Из данных значений следует обратить внимание на резкое отличие значения постоянной  от типичного значения удельной энергии связи
от типичного значения удельной энергии связи 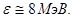 Удельную энергию связи
Удельную энергию связи  , должно было бы иметь гипотетическое ядро больших размеров, состоящее из одинакового числа протонов и нейтронов, при отсутствии кулоновского взаимодействия между протонами.
, должно было бы иметь гипотетическое ядро больших размеров, состоящее из одинакового числа протонов и нейтронов, при отсутствии кулоновского взаимодействия между протонами.
Полная энергия ядра (масса):
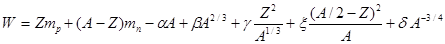 , (3.6)
, (3.6)
где массы протона и нейтрона выражены в единицах энергии (МэВ).
Формула (3.6) называется формулой Вейцзеккера. Данная формула хорошо описывает экспериментальные значения энергий связи. Однако она не объясняет результаты ядерной спектроскопии, магнитные моменты и спины ядер, существование особо стабильных ядер (магические ядра).
