Статическое рассеяние света
Теоретическая часть
Среди методов исследования полимеров в растворе одним из важнейших фактором является статическое светорассеяние, которое дает информацию о средневесовой молекулярной массе (Mw), статистических размерах макромолекул, а также термодинамическом качестве растворителя.
Однородная среда не способна рассеивать свет, так как вторичные световые волны, испускаемые всеми ее элементарными объемами, полностью гасят друг друга при интерференции. Рассеяние света в чистой (оптически «пустой») жидкости обусловлено флуктуациями плотности в объемах, малых по сравнению с кубом длины световой волны λ03. В растворах к этому добавляется рассеяние света на флуктуациях концентрации с растворенного вещества в объемах того же порядка величины. С последним связана интенсивность избыточного рассеяния, представляющая разность между интенсивностями рассеяния раствора и чистого растворителя.
Для удобства рассматривают приведенную интенсивность Iθ, не зависящую от выбора интенсивности первичного светового пучка и объема раствора
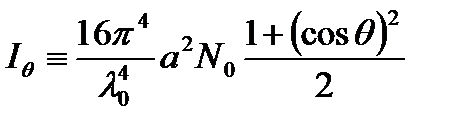 , (2.1)
, (2.1)
где α – поляризуемость молекулы, N0 – число растворенных молекул в единице раствора, θ – угол рассеяния. Заменяя дробь  на фактор рассеяния Дебая P(θ), получаем
на фактор рассеяния Дебая P(θ), получаем
 (2.2)
(2.2)
Число растворенных молекул в единице объема N0 выразим через концентрацию с, молекулярную массу М и число Авогадро NA:  .
.
Выразив поляризуемость молекулы α через диэлектрическую проницаемость и связав последнюю с показателем преломления растворителя n0и раствора n, можно преобразовать выражение (2.2) для вертикально поляризованного света в
 , (2.3)
, (2.3)
где
 (2.4)
(2.4)
оптическая постоянная, а величину 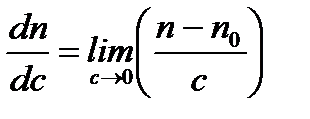 называют инкрементом показателя преломления.
называют инкрементом показателя преломления.
Уравнение рассеяния раствора (2.3) позволяет, в принципе, определить средневесовую молекулярную массу Мw невзаимодействующих молекул, измерив коэффициент рассеяния Iθ (в частности, для θ = 90˚) при одной концентрации раствора с:
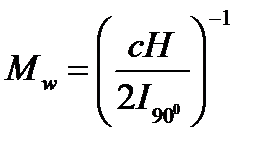 (2.5)
(2.5)
В подавляющем большинстве полимерных растворов сказывается влияние межмолекулярного взаимодействия. Выражение для I90˚ раствора взаимодействующих молекул было получено Эйнштейном на основе термодинамических соображений:
 (2.6)
(2.6)
Осмотическое давление раствора П как функцию его концентрации с можно выразить в виде степенного ряда:
 , (2.7)
, (2.7)
где Аi – вириальные коэффициенты раствора, первый из которых А1 равен 1/Мw. Тогда
 (2.8)
(2.8)
P(90o) = 1.
Для идеального раствора, т.е. раствора, где скомпенсированы межмолекулярные взаимодействия, все вириальные коэффициенты, кроме первого, обращаются в нуль. В этом случае последнее выражение сводится к (2.6). Величина А2характеризует термодинамическое взаимодействие полимера и растворителя. Если А2> 0, то растворитель хороший, отрицательное значение А2 свидетельствует о плохом темодинамическом качестве растворителя.
