Большинство из векторных угловых величин относятся к классу аксиальных (axe (лат.) – ось) векторов

Аксиальные векторы (псевдовекторы) – это векторы, характеризующие вращение.

В отличие от полярных векторов аксиальные вектора всегда направлены вдоль оси вращения и не имеют конкретной точки приложения. При переходе от правой системы координат к левой псевдовектора изменяют свое направление на противоположное.

Полярные вектора при переходе от правой системы координат к левой всегда сохраняют свое направление неизменным.

Векторное произведение двух полярных векторов дают псевдовектор.

Аксиальные векторы могут быть отложены от любой точки на оси вращения.

Угловая скорость.

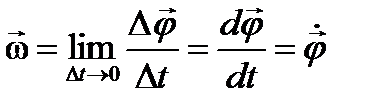
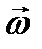Угловая скорость – ВФВ, характеризующая быстроту поворота и равная пределу отношения приращения вектора углового перемещения к бесконечно малому промежутку времени, в течение которого это приращение произошло:

Размерность угловой скорости [w] = 1 рад/с

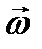Угловая скорость является псевдовектором (аксиальным вектором) как и угловое перемещение.

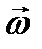
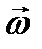Угловая скорость направлена вдоль оси вращения и ее направление всегдасовпадает с направлением вектора углового перемещения

Направление вектора угловой скорости определяется правилом правого винта (правилом буравчика).

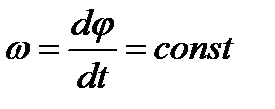Вращение тела вокруг неподвижной оси называется равномерным, если модуль угловой скорости постоянен:

В случае равномерного вращения угол поворота тела прямо пропорционален времени его вращения t:

При равномерном вращении угловая скорость ω показывает, на какой угол поворачивается тело за единицу времени.

Для характеристики равномерного вращения вводятся две величины – период T обращения и частота n обращения.

Период T обращения– это время за которое тело делает один полный оборот.

Размерность периода обращения [T ] = 1 с

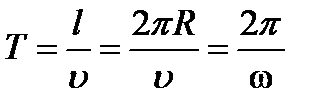Найдем связь периода T обращения с угловой скоростью.

Величина равная обратной величиной периода вращения (обращения) называется частотой вращения или числом оборотом в единицу времени.

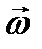Частота n обращения – это число оборотов совершаемое телом за единицу времени, равномерно вращающегося с угловой скоростью .

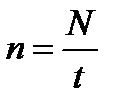
Размерность частоты обращения [n] = 1 с^-1

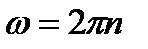Частота n обращения обратно периоду T обращения:

Угловая скорость связана с частотой обращения по формуле:

Угловое ускорение.

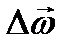
Угловое ускорение –ВФВ, характеризующая быстроту изменения вектора угловой скорости и равная пределу отношения приращения вектора угловой скорости к бесконечно малому промежутку времени , в течение которого произошло приращение скорости:

Угловое ускорение является псевдовектором (аксиальным вектором)как угловая скорость и угловое перемещение.

Размерность углового ускорения [e ] = 1 рад/с².

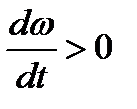
Вектор углового ускорения может принимать всего два направления:

1) 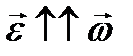Если (ускоренное вращение), то

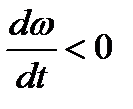
2) 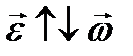Если (замедленное вращение), то