Кинематика вращательного движения
Вращательным движением твердоготела называется движение при котором все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Ось вращения может проходить как через вращающееся тело, так и находиться вне этого тела.
Вращающееся тело имеет одну степень свободы вокруг неподвижной оси.
Положение тела в пространстве определяется значением угла поворота вокруг оси вращения.
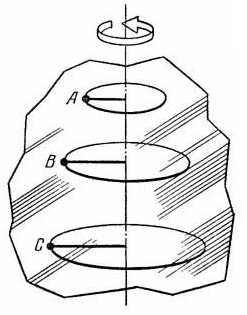
Рассмотрим вращение м.т. по окружности радиуса R.
Пусть в начальный момент времени t0 м.т. находится в положении M и ее скорость равна u0.
Спустя промежуток времени dt = t1 – t0 м.т. пройдет по окружности путь l и окажется в положении M1.
Радиус-вектор точки, проведенный из центра O окружности, повернется на угол j.
Угол j называется угловым путем (углом поворота).
Размерность углового пути [j] = 1 рад.
Из геометрии известно, что длина дуги, на которую опирается центральный угол MOM1, равна:l = jR
Положение тела в пространстве полностью определяется значением угла поворота вокруг оси вращения из некоторого, условно выбранного начального положения этого тела.
Для описания вращательного движения тела неудобно пользоваться понятиями кинематики, как:
1) перемещение;
2) пройденный путь;
3) скорость;
4) ускорение.
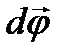 В случае вращательного движения мерой перемещения всего тела за малый промежуток времени dt служит вектор элементарного угла поворота тела .
В случае вращательного движения мерой перемещения всего тела за малый промежуток времени dt служит вектор элементарного угла поворота тела .
18. Момент инерции материальной точки и момент инерции твердого тела. Теорема Штейнера. Моменты инерции.
Момент инерции.
Рассмотрим твердое тело вращающееся вокруг неподвижной оси OZ.
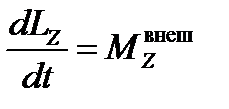 Основной закон динамики тела, вращающегося вокруг неподвижной оси OZ, имеет вид:
Основной закон динамики тела, вращающегося вокруг неподвижной оси OZ, имеет вид:
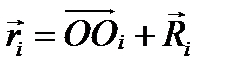 Найдем связь между моментом импульса Lz и угловой скоростью ω.
Найдем связь между моментом импульса Lz и угловой скоростью ω.
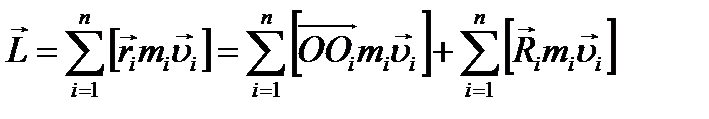 Момент импульса тела относительно начала координат О.
Момент импульса тела относительно начала координат О.
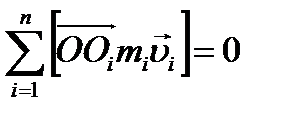 Моменты импульсов точек лежащих на оси вращения равны нулю:
Моменты импульсов точек лежащих на оси вращения равны нулю:
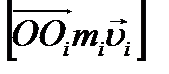
Так как вектор перпендикулярен оси OZ
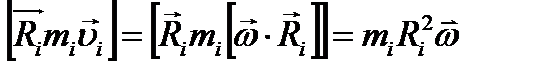 Вектор направлен оси OZ.
Вектор направлен оси OZ.
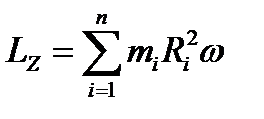
Таким образом,
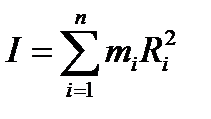 Величина, равная сумме произведений масс всех материальных точек, образующих механическую систему, на квадраты их расстояний от данной оси вращения, называется моментом инерции системы относительно этой оси:
Величина, равная сумме произведений масс всех материальных точек, образующих механическую систему, на квадраты их расстояний от данной оси вращения, называется моментом инерции системы относительно этой оси:
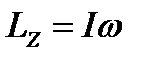 Таким образом, момент импульса тела относительно оси OZ равен:
Таким образом, момент импульса тела относительно оси OZ равен:
где I – момент инерции тела относительно оси вращения OZ.
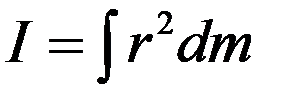 Если известен закон распределения массы тела, то момент инерции твердого тела можно определить по формуле:
Если известен закон распределения массы тела, то момент инерции твердого тела можно определить по формуле:
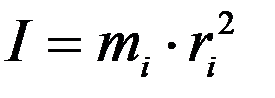 Моментом инерции м.т. относительно некоторой осиназывают скалярную физическую величину, равную произведению массы материальной точки на квадрат расстояния до оси вращения:
Моментом инерции м.т. относительно некоторой осиназывают скалярную физическую величину, равную произведению массы материальной точки на квадрат расстояния до оси вращения:
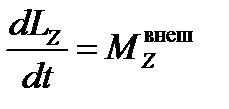
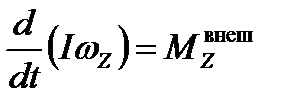
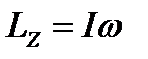
Уравнение с учетом можно написать в виде:
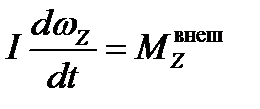 В процессе вращения считается, что I=const, т.е. тело не деформируется:
В процессе вращения считается, что I=const, т.е. тело не деформируется:
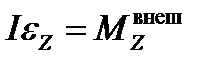
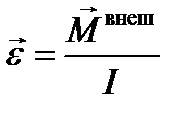 Из уравнения видно, что угловое ускорение обратно пропорционально моменту инерции. Следовательно, момент инерции тела относительно оси является мерой инертности тела в его вращении вокруг этой оси.
Из уравнения видно, что угловое ускорение обратно пропорционально моменту инерции. Следовательно, момент инерции тела относительно оси является мерой инертности тела в его вращении вокруг этой оси.
Основное уравнение динамики вращательного движения:
В динамике вращательного движения момент инерции играет ту же роль, что и масса в динамике поступательного движения. Момент инерции определяет величину углового ускорения, получаемого телом под действием данного момента силы. Величина момента инерции определяется не только массой тела, но и распределением этой массы относительно оси вращения. Одно и то же тело может иметь различные моменты инерции относительно разных осей, и тела разной массы могут при определенном распределении масс в них иметь одинаковые моменты инерции.
