Каноническое распределение Гиббса
Удобно записать теорему Лиувилля в виде:
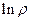 - есть интеграл движения, точнее
- есть интеграл движения, точнее 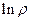 есть функция различных интегралов движения.
есть функция различных интегралов движения.
Поместим систему в жёсткий неподвижный ящик, тогда, т.к. не может двигаться так: 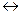 , то нет сохранения импульса. И так как не может вращаться , то нет сохранения момента импульса. Тогда осталось сохранение энергии, т.е. можем записать:
, то нет сохранения импульса. И так как не может вращаться , то нет сохранения момента импульса. Тогда осталось сохранение энергии, т.е. можем записать:
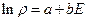
Само распределение пишется:
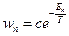
Это каноническое распределение Гиббса; для квантового случая навешивается 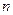 - номер квантового состояния.
- номер квантового состояния. 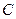 - константа, не зависящая от состояния
- константа, не зависящая от состояния 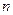 , которая находится из условия
, которая находится из условия 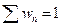 .
.
Здесь 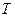 - температура в энергетической шкале – это удобно в теории. Хотя на практике
- температура в энергетической шкале – это удобно в теории. Хотя на практике 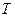 измеряют в градусах.
измеряют в градусах.
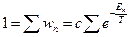 ,
, 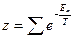
тогда 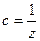 .
.
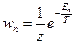
 Система 1 и термостат 2 образуют замкнутую систему. Здесь присутствует микроканоническое распределение.
Система 1 и термостат 2 образуют замкнутую систему. Здесь присутствует микроканоническое распределение.
На базе микроканонического распределения строят каноническое распределение.
Также можно получить каноническое распределение системы через принцип возрастания энтропии.
Рассмотрим систему 1, и считаем что состояние стационарное.
Найдём условие экстремума функции 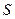 .
.
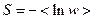
Мы используем 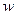 - квантовые функции, т.к. это удобнее, чем использовать
- квантовые функции, т.к. это удобнее, чем использовать 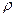 . При использовании
. При использовании 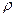 вылезает константа из-за размерности
вылезает константа из-за размерности 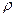 .
. 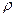 - это размерная величина, а логарифм надо брать от безразмерной величины, каковой и является
- это размерная величина, а логарифм надо брать от безразмерной величины, каковой и является 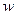 .
.
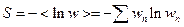
Второе начало термодинамики:
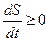
т.е. если система выведена из состояния равновесия, то она идёт в развитии с увеличением 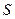 , поэтому:
, поэтому:
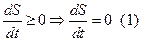 - имеем условие экстремума
- имеем условие экстремума
Отсюда имеем задачу поиска экстремума функции 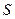 .
.
Вероятность удовлетворяет условию нормировки:
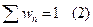 -это условие для отыскания экстремума
-это условие для отыскания экстремума 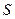
Задача (1) и (2) является задачей поиска условного экстремума.
Однако с помощью метода неопределённых множителей Лагранжа можно найти экстремум 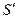 . Для этого вводится функция
. Для этого вводится функция
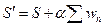 , где
, где 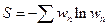
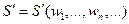
Найдём производную 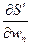 :
:
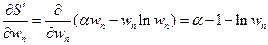
здесь остальные члены при дифференцировании обращаются в нуль.
Найдём вторые производные:
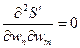 , при
, при 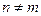
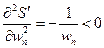 - это выражение отрицательное
- это выражение отрицательное
Стало быть, мы имеем максимум, так как вторая производная меньше нуля.
Тогда из условия 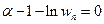 находим само условие экстремума.
находим само условие экстремума.
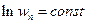
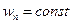
константа находится из условия нормировки:
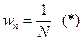 , где
, где 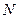 - число всех состояний
- число всех состояний
Выражение (*) есть принцип равной вероятности для замкнутой системы; это есть микроканоническое распределение.
Теперь найдём экстремум энтропии 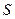 при двух условиях, а именно при:
при двух условиях, а именно при:
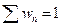 и
и 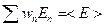
Переходим от условного экстремума энтропии к безусловному экстремуму функции 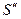 :
:
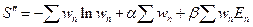
Берём производные:
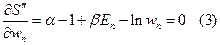
(3) - это условие экстремума 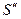 , это одно и то же что условие экстремума для
, это одно и то же что условие экстремума для 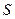 при условиях
при условиях 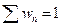 и
и 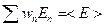 .
.
Обозначим 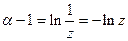 , тогда:
, тогда:
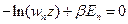
Отсюда для 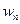 имеем:
имеем:
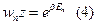
Постоянная 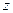 находится из условия нормировки:
находится из условия нормировки:
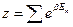 (5)
(5)
Выражение (5) называется статистической суммой. А выражение (4) – это каноническое распределение Гиббса.
Это распределение относится к системе:
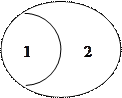 Где 1 находится в тепловом контакте с термостатом 2.
Где 1 находится в тепловом контакте с термостатом 2.
Микроканоническое распределение мы получали для замкнутых систем, где 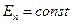 , т.е. условия
, т.е. условия 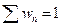 и
и 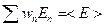 вырождаются в одно
вырождаются в одно 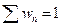 . И для микроканонического распределения мы получили:
. И для микроканонического распределения мы получили:
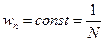
А каноническое распределение получили, когда система 1 была в тепловом контакте с термостатом 2:
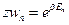
Константа 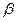 находится из условия
находится из условия 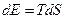 , т.е.
, т.е. 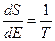 - здесь
- здесь 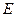 среднее значение энергии, т.к. у нас случай термодинамики.
среднее значение энергии, т.к. у нас случай термодинамики.
Найдём связь энтропии с энергией:
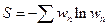
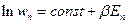
Тогда:
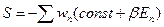
Используем условия 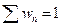 и
и 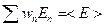 :
:
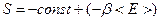
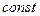 - это константа по энергии.
- это константа по энергии.
В термодинамике 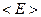 - это наблюдаемая величина, поэтому пишут эту величину просто
- это наблюдаемая величина, поэтому пишут эту величину просто 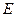 , т.к.
, т.к. 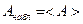 (
( 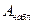 - из эксперимента, а
- из эксперимента, а 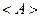 - из теории).
- из теории).
Тогда:
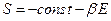
Отсюда имеем 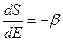 , но ведь
, но ведь 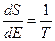 , а значит:
, а значит:
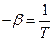
И мы определили второй неопределённый множитель Лагранжа.
Каноническое распределение Гиббса принимает вид:
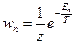 , где
, где 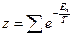
Аналогично пишут для 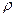 , но тогда вместо статистической суммы
, но тогда вместо статистической суммы 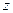 будет интеграл.
будет интеграл.
Здесь 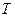 - температура в энергетических единицах.
- температура в энергетических единицах.
