Гармонические колебания и их характеристики
Довольно распространенный тип движения механических систем представляют собой так называемые малые колебания, которые система совершает вблизи своего положения устойчивого равновесия
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания различают механические и электромагнитные. Различные колебательные процессы описываются одинаковыми характеристиками, процессами и уравнениями.
Системы, в которых можно наблюдать периодическое движение называются колебательными. Периодическое движение, один раз возникнув, может продолжаться без постороннего действия внешних периодических сил. Колебания, происходящие в системе, на которую не действуют внешние силы, называются свободными.
Хорошо известно, что в ряде случаев тело, получившее некоторое возмущение, после этого совершает колебания. Хотя такие свободные колебания сами по себе обычно не представляют особенного интереса для техники, знакомство с ними необходимо, поскольку их роль косвенно чрезвычайно важна.
Свободные колебания совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.
Рассмотрим эти движения в наиболее простом случае, когда система имеет всего лишь одну степень свободы. Это значит, что для однозначного определения положения колеблющейся системы в таком пpостpанстве достаточно задать всего одно число. Это не обязательно должна быть декартова координата, а в зависимости от условий задачи может оказаться более удобным выбор какой-то другой величины. Такая величина, однозначно хаpактеpизующая положение системы, называется ее обобщенной координатой.
Простейшим типом колебания являются гармонические колебания, где зависимость координаты х от времени задается уравнением
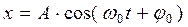 , (19.1)
, (19.1)
где А – амплитуда - максимальное значение колеблющейся величины,
w0 - циклическая частота является основной характеристикой колебаний, не зависящей от начальных условий движения, и в частности, от энергии,
j0 - начальная фаза колебаний при t=0,
φ = (w0t +j0)- фаза колебаний в момент времени t.
Фаза показывает, состояние колеблющейся системы в данный момент времени.
Определенные состояния системы повторяются через промежуток времени называемый периодом колебания Т, время за которое фаза колебаний получает приращение равное 2p
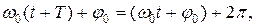 (19.2)
(19.2)
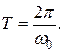
Таким образом, период колебаний Т – это наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебания. К примеру, если система совершает n колебанийза время t , то период Т определяется, как  . Период колебаний в системе СИ измеряется в секундах [T]= c.
. Период колебаний в системе СИ измеряется в секундах [T]= c.
Величина обратная периоду колебаний называется частотой, т.е. число колебаний в единицу времени. В системе СИ единица измерения частоты – Герц [ν]=[Гц]
 . (19.3)
. (19.3)
При подстановке (19.2) в (19.3) получим связь циклической частоты с частотой, а также и с периодом
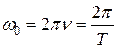 . (19.4)
. (19.4)
