Основные физические величины и законы
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) 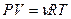 ,
,
где 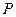 – давление газа (
– давление газа ( 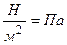 );
);  – объем занимаемый газом (
– объем занимаемый газом (  );
);
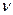 – количество молей газа;
– количество молей газа; 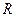 – универсальная постоянная,
– универсальная постоянная,  ;
;
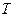 – абсолютная температура газа,
– абсолютная температура газа,  .
.
Для однородного газа
 ,
,
где 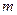 – масса газа (кг);
– масса газа (кг); 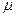 – масса моля (молярная масса)газа (
– масса моля (молярная масса)газа ( 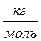 ).
).
Для смеси газов
 .
.
Парциальное давление 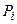 «i» компоненты смеси газов находят из
«i» компоненты смеси газов находят из
 .
.
Основное уравнение молекулярно-кинетической теории идеальных газов
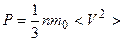 ,
,
где 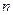 – концентрация молекул,
– концентрация молекул,  ;
; 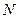 – общее число молекул газа;
– общее число молекул газа; 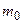 – масса одной молекулы (кг);
– масса одной молекулы (кг); 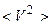 – средний квадрат скоростей молекул (
– средний квадрат скоростей молекул (  );
);  – объем, занимаемый газом (
– объем, занимаемый газом (  ).
).
Средняя кинетическая энергия молекулы
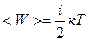 ,
,
где 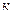 – постоянная Больцмана,
– постоянная Больцмана, 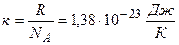 ;
; 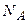 – число Авогадро (число молекул в одном моле);
– число Авогадро (число молекул в одном моле);  – число степеней свободы молекул. Одноатомный газ
– число степеней свободы молекул. Одноатомный газ 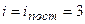 , двухатомные молекулы
, двухатомные молекулы 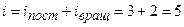 , многоатомные молекулы
, многоатомные молекулы  .
.
Средняя скорость молекул
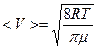 .
.
Средняя квадратичная скорость молекул
 .
.
Средняя длина свободного пробега молекул
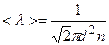 ,
,
где 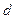 – эффективный диаметр молекулы.
– эффективный диаметр молекулы.
Внутренняя энергия идеального газа
 .
.
Работа, совершаемая газом при изменении объема от 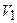 до
до 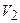
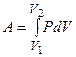 .
.
Работа газа в изопроцессах:
изохорный ( 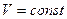 ),
), 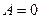 ;
;
изобарный (  ),
),  ;
;
изотермический 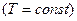 ,
,  .
.
Теплота, полученная (отданная) газом
 ,
,
где 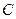 – удельная теплоемкость (
– удельная теплоемкость (  ).
).
Первое начало термодинамики
 ,
,
где 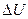 – изменение внутренней энергии.
– изменение внутренней энергии.
Удельная теплоемкость газа при постоянном объеме
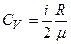 .
.
Удельная теплоемкость газа при постоянном давлении
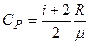 .
.
Уравнение адиабатического ( 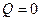 ) процесса – уравнение Пуассона
) процесса – уравнение Пуассона
 ,
,
где  – показатель адиабаты.
– показатель адиабаты.
Работа газа при адиабатическом процессе
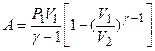 ;
;
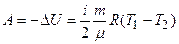 .
.
Коэффициент полезного действия тепловой машины
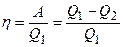 ,
,
где 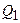 – количество теплоты, полученное системой за один цикл;
– количество теплоты, полученное системой за один цикл; 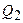 – количество теплоты, отданное системой за один цикл;
– количество теплоты, отданное системой за один цикл;  – работа, совершаемая за один цикл.
– работа, совершаемая за один цикл.
Коэффициент полезного действия цикла Карно (идеальной тепловой машины) 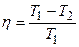 ,
,
где 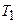 – температура нагревателя;
– температура нагревателя; 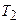 – температура охладителя.
– температура охладителя.
Пример 1.Один баллон емкостью 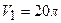 содержит азот под давлением
содержит азот под давлением  , другой баллон емкостью
, другой баллон емкостью 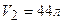 содержит кислород под давлением
содержит кислород под давлением  . Оба баллона были соединены между собой и оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления
. Оба баллона были соединены между собой и оба газа смешались, образовав однородную смесь (без изменения температуры). Найти парциальные давления  и
и 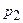 обоих газов в смеси и полное давление
обоих газов в смеси и полное давление 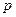 смеси.
смеси.
Дано:  ;
;
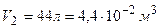 ;
;
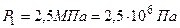 ;
;
 ;
;
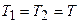 .
.
Найти: 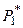 ,
,  ,
, 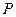 .
.
Решение. Парциальное давление азота 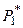 и кислорода
и кислорода  находим из уравнений
находим из уравнений

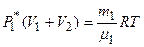
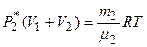 . (1.1)
. (1.1)
В начальных состояниях уравнения Менделеева-Клапейрона для азота и кислорода есть
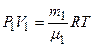
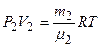 . (1.2)
. (1.2)
 Учитывая формулы (1.2), уравнения (1.1) принимают вид
Учитывая формулы (1.2), уравнения (1.1) принимают вид

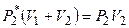 .
.
Получаем
 ;
;  .
.
Подставим заданные численные значения
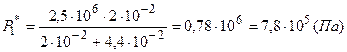 ,
,
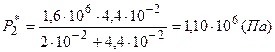 .
.
Полное давление смеси газов равно сумме парциальных
 ;
;
 .
.
Пример 2. Определить среднюю кинетическую энергию  вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа
вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул одного киломоля этого газа  .
.
Дано: 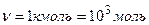 ;
;
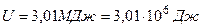 .
.
Найти:  .
.
Решение. Средняя кинетическая энергия вращательного движения молекулы
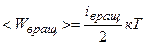 . (2.1)
. (2.1)
где  – число степеней свободы вращательного движения молекулы.
– число степеней свободы вращательного движения молекулы.
Суммарная кинетическая энергия всех молекул газа (внутренняя энергия идеального газа)
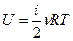 , (2.2)
, (2.2)
где  – общее число степеней свободы молекулы (поступательного и вращательного движений).
– общее число степеней свободы молекулы (поступательного и вращательного движений).
Отсюда  . (2.3)
. (2.3)
Подставляя формулу (2.3) в уравнение (2.1), получим
 .
.
Учитывая, что  ,
,
где 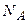 – число Авокадро,
– число Авокадро, 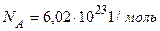 , окончательно получаем
, окончательно получаем
 .
.
Подставим численные значения величин, учитывая, что для двухатомного газа
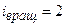 ;
; 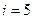 .
.
 .
.
Пример 3.Определить среднюю длину свободного пробега < 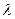 > и среднее число столкновений
> и среднее число столкновений  молекулы гелия за 1с при температуре
молекулы гелия за 1с при температуре
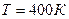 и давлении
и давлении  .
.
Дано: 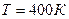 ;
;  ;
;
 ;
;
 .
.
Найти:  ,
,  .
.
Решение. Средняя длина свободного пробега молекул определяется формулой
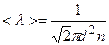 , (3.1)
, (3.1)
где 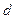 – эффективный диаметр молекулы. Гелий – газ одноатомный. Диаметр гелия находим из справочных таблиц.
– эффективный диаметр молекулы. Гелий – газ одноатомный. Диаметр гелия находим из справочных таблиц. 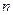 – число атомов в единице объема.
– число атомов в единице объема.
Из уравнения Менделеева-Клапейрона в виде 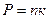 T находим
T находим
 , (3.2)
, (3.2)
где 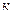 – постоянная Больцмана,
– постоянная Больцмана,  .
.
Перепишем уравнение (3.1) с учетом формулы (3.2)
 .
.
Подставим численные значения
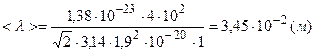 .
.
Среднее число столкновений атомов за единицу времени можно найти из формулы
 .
.
Средняя скорость 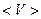 – атомов определяется формулой
– атомов определяется формулой
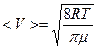 .
.
Таким образом
 .
.
Подставим численные значения
 (1/с).
(1/с).
Пример 4.Кислород массой  занимает объем
занимает объем 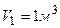 и находится под давлением
и находится под давлением 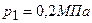 . При нагревании газ расширился при постоянном давлении до объема
. При нагревании газ расширился при постоянном давлении до объема  , а затем его давление возросло до
, а затем его давление возросло до 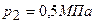 при неизменном объеме. Найти изменение внутренней энергии
при неизменном объеме. Найти изменение внутренней энергии 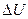 газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
Дано:  ;
; 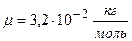 ;
;
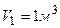 ;
;  ;
;
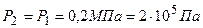 ;
;
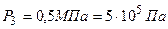 .
.
Найти: 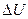 ,
,  ,
,  .
.
Решение. Изменение внутренней энергии газа выражается формулой
 .
.
В данном случае  .
.
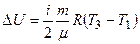 , (4.1)
, (4.1)
где i – число степеней свободы молекул газа ( для двухатомных молекул кислорода i = 5 ).
Температуры газа в каждом состоянии найдем, используя уравнение Менделеева - Клапейрона
 .
.
Отсюда  .
.
Подставим численные значения параметров каждого из трех состояний
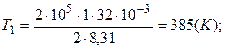
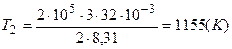 ;
;
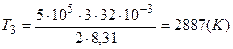 .
.
Подставляя в выражение (4.1) числовые значения находим
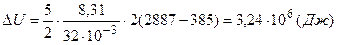 .
.
Работа расширения газа при постоянном давлении выражается формулой
 .
.
Работа газа при 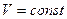 равна нулю.
равна нулю.
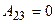 .
.
Таким образом, полная работа, совершаемая газом, равна
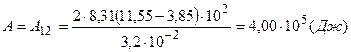 .
.
Согласно первому началу термодинамики теплота Q, переданная газу, равна сумме изменения внутренней энергии 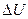 и работы А:
и работы А:  , следовательно,
, следовательно,
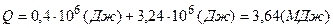 .
.
График процесса приведен на рисунке 5.
 |
Рисунок 5.
Пример 5.Идеальная тепловая машина работает по циклу Карно. Температура нагревателя в 2 раза выше температуры охладителя. Работа цикла
1 кДж. Какое количество теплоты передано охладителя за один цикл?
Дано:  ;
;
 .
.
Найти: 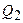 .
.
Решение. Количество теплоты, отданное охладителю, равно разности между теплотой, полученной газом от нагревателя и совершенной им работой
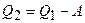 . (5.1)
. (5.1)
Из определения К.П.Д. тепловой машины

следует 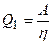 .
.
Теперь уравнение (5.1) примет вид
 . (5.2)
. (5.2)
Для идеальной тепловой машины К.П.Д. равно
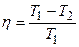 .
.
По условию задачи  .
.
Значит 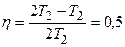 . (5.3)
. (5.3)
Подставляя формулу (5.3) в уравнение (5.2), и с учетом численного значения  , получаем
, получаем
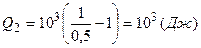 .
.
Задачи
2.01. Сосуд емкостью  содержит азот массой
содержит азот массой 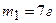 и водород массой
и водород массой  при температуре
при температуре 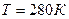 . Определить давление
. Определить давление 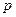 смеси газов.
смеси газов.
2.02. Два сосуда одинаковой емкости содержат кислород. В одном сосуде давление  и температура
и температура 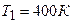 , в другом
, в другом 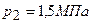 ,
,  . Сосуды соединили трубкой и охладили находящийся в них кислород до температуры
. Сосуды соединили трубкой и охладили находящийся в них кислород до температуры 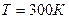 . Определить установившееся давление
. Определить установившееся давление 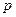 в сосудах.
в сосудах.
2.03. Баллон емкостью 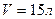 содержит смесь водорода и азота при температуре
содержит смесь водорода и азота при температуре 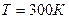 и давлении
и давлении  . Масса смеси
. Масса смеси 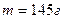 . Определить массу m1 водорода и массу m2 азота.
. Определить массу m1 водорода и массу m2 азота.
2.04. Определить массу m1 одной молекулы сероуглерода CS2. Принимая, что молекулы в жидкости имеют шарообразную форму и расположены вплотную друг к другу, определить диаметр d молекулы.
2.05. Найти плотность ρ газовой смеси, состоящей по массе из одной части водорода и восьми частей кислорода при давлении  и температуре
и температуре 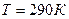 .
.
2.06. В баллоне емкостью  находится аргон под давлением
находится аргон под давлением
 и температуре
и температуре  . Когда из баллона было взято некоторое количество аргона, давление в баллоне понизилось до
. Когда из баллона было взято некоторое количество аргона, давление в баллоне понизилось до  , а температура установилась
, а температура установилась  . Определить массу т аргона, взятого из баллона.
. Определить массу т аргона, взятого из баллона.
2.07. В баллоне емкостью  находится водород при нормальных условиях. После того как в баллон было дополнительно введено некоторое количество гелия, давление в баллоне возросло до
находится водород при нормальных условиях. После того как в баллон было дополнительно введено некоторое количество гелия, давление в баллоне возросло до  , а температура не изменилась. Определить массу гелия, введенного в баллон.
, а температура не изменилась. Определить массу гелия, введенного в баллон.
2.08. Вычислить плотность ρ кислорода, находящегося в баллоне под давлением 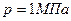 при температуре
при температуре 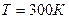 .
.
2.09. Газовая смесь, состоящая из кислорода и азота, находится в баллоне под давлением 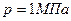 . Считая, что масса кислорода составляет 20% от массы смеси, определить парциальные давления p1 и р2 отдельных газов.
. Считая, что масса кислорода составляет 20% от массы смеси, определить парциальные давления p1 и р2 отдельных газов.
2.10. Баллон емкостью  заполнен азотом. Температура азота
заполнен азотом. Температура азота 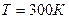 . Когда часть азота израсходовали, давление в баллоне понизилось на
. Когда часть азота израсходовали, давление в баллоне понизилось на 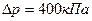 . Определить массу
. Определить массу  израсходованного азота. Процесс считать изотермическим.
израсходованного азота. Процесс считать изотермическим.
2.11. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами. Масса каждой пылинки
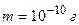 . Температура газа
. Температура газа  . Определить средние квадратичные скорости
. Определить средние квадратичные скорости  , а также средние кинетические энергии
, а также средние кинетические энергии  поступательного движения молекул азота и пылинок.
поступательного движения молекул азота и пылинок.
2.12. Удельные теплоемкости некоторого газа:  и
и
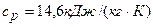 . Определить киломольные теплоемкости.
. Определить киломольные теплоемкости.
2.13. Баллон емкостью 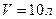 содержит азот массой
содержит азот массой  . Определить среднюю длину свободного пробега молекул.
. Определить среднюю длину свободного пробега молекул.
2.14. Найти среднюю квадратичную скорость молекул газа, плотность которого при давлении 750 мм рт. ст. равна  . Чему равна молярная масса этого газа, если значение плотности дано для температуры 170С?
. Чему равна молярная масса этого газа, если значение плотности дано для температуры 170С?
2.15. Найти диаметр d молекул водорода, если для водорода при нормальных условиях длина свободного пробега молекул 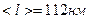 .
.
2.16. Газ занимает объем 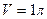 под давлением
под давлением 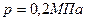 . Определить кинетическую энергию поступательного движения всех молекул, находящихся в данном объеме.
. Определить кинетическую энергию поступательного движения всех молекул, находящихся в данном объеме.
2.17. Некоторый газ находится при температуре  в баллоне емкостью
в баллоне емкостью  под давлением
под давлением 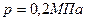 . Теплоемкость этого газа при постоянном объеме
. Теплоемкость этого газа при постоянном объеме 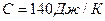 . Определить отношение теплоемкостей
. Определить отношение теплоемкостей 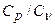 .
.
2.18. Определить среднее число соударений  в секунду молекулы водорода при температуре
в секунду молекулы водорода при температуре 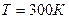 и давлении
и давлении 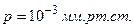 .
.
2.19. Сосуд емкостью 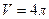 содержит
содержит  некоторого газа под давлением
некоторого газа под давлением 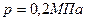 . Определить среднюю квадратичную скорость молекул газа.
. Определить среднюю квадратичную скорость молекул газа.
2.20. Вычислить теплоемкость при постоянном объеме двухатомного газа, заключенного в сосуд 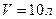 при нормальных условиях.
при нормальных условиях.
2.21. В закрытом сосуде объемом 10 л находится воздух при давлении  . Какое количество теплоты надо сообщить воздуху, чтобы повысить давление в сосуде в 5 раз?
. Какое количество теплоты надо сообщить воздуху, чтобы повысить давление в сосуде в 5 раз?
2.22. При изотермическом расширении одного моля водорода, имевшего температуру 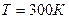 , затрачена теплота
, затрачена теплота  . Во сколько раз увеличился объем газа?
. Во сколько раз увеличился объем газа?
2.23. В цилиндре под поршнем находится азот массой 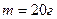 . Газ был нагрет от температуры
. Газ был нагрет от температуры 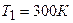 до температуры
до температуры 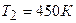 при постоянном давлении. Определить теплоту Q, переданную газу, совершенную газом работу А и приращение
при постоянном давлении. Определить теплоту Q, переданную газу, совершенную газом работу А и приращение 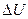 внутренней энергии.
внутренней энергии.
2.24. При адиабатическом сжатии кислорода массой 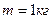 совершена работа
совершена работа  . Какова конечная температура Т2 газа, если до сжатия кислород находился при температуре
. Какова конечная температура Т2 газа, если до сжатия кислород находился при температуре 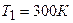 ?
?
2.25. Азот находится в закрытом сосуде объемом 3 л при температуре 270С и давлении 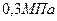 . После нагревания давление в сосуде повысилось до
. После нагревания давление в сосуде повысилось до 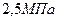 . Определить: 1). температуру азота после нагревания; 2). количество теплоты, сообщенное азоту.
. Определить: 1). температуру азота после нагревания; 2). количество теплоты, сообщенное азоту.
2.26. При изотермическом расширении водорода массой  объем газа V увеличился в два раза. Определить работу А расширения, совершенную газом, если температура газа
объем газа V увеличился в два раза. Определить работу А расширения, совершенную газом, если температура газа 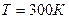 . Определить теплоту Q, переданную при этом газу.
. Определить теплоту Q, переданную при этом газу.
2.27. Из баллона, содержащего водород под давлением  при температуре
при температуре 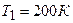 , выпустили половину находившегося в нем газа. Считая процесс адиабатическим, определить конечные температуру T2 и давление р2.
, выпустили половину находившегося в нем газа. Считая процесс адиабатическим, определить конечные температуру T2 и давление р2.
2.28. При изотермическом расширении 2 м3 газа давление его меняется от 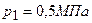 до
до 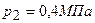 . Найти совершенную при этом работу.
. Найти совершенную при этом работу.
2.29. Гелий находится в закрытом сосуде объемом 2 л при температуре 200 С и давлении  . 1). Какое количество теплоты надо сообщить гелию, чтобы повысить его температуру на 1000 С? 2). Какова будет средняя квадратичная скорость его молекул при новой температуре? 3). Какое установится давление? 4). Какова будет плотность гелия? 5). Какова будет энергия теплового движения его молекул?
. 1). Какое количество теплоты надо сообщить гелию, чтобы повысить его температуру на 1000 С? 2). Какова будет средняя квадратичная скорость его молекул при новой температуре? 3). Какое установится давление? 4). Какова будет плотность гелия? 5). Какова будет энергия теплового движения его молекул?
2.30. Для нагревания некоторой массы газа на 500 С при постоянном давлении необходимо затратить 160 кал. Если эту же массу газа охладить на 1000 с при постоянном объеме, то выделяется 240 кал. Какое число степеней свободы имеют молекулы этого газа?
2.31. Газ совершает цикл Карно. Работа изотермического расширения газа 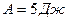 . Определить работу изотермического сжатия, если термический к. п. д. цикла
. Определить работу изотермического сжатия, если термический к. п. д. цикла  .
.
2.32. Совершая цикл Карно, газ отдал охладителю теплоту 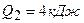 . Работа цикла
. Работа цикла 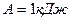 . Определить температуру нагревателя, если температура охладителя
. Определить температуру нагревателя, если температура охладителя 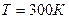 .
.
2.33. Газ совершает цикл Карно. Абсолютная температура охладителя 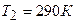 . Во сколько раз увеличится к. п. д. цикла, если температура нагревателя повысится от
. Во сколько раз увеличится к. п. д. цикла, если температура нагревателя повысится от  до
до  ?
?
2.34. Газ совершает цикл Карно. Температура нагревателя 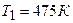 , охладителя
, охладителя 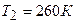 . При изотермическом расширении газ совершил работу
. При изотермическом расширении газ совершил работу
 . Определить термический к. п. д. η цикла, а также теплоту Q2, которую газ отдает охладителю при изотермическом сжатии.
. Определить термический к. п. д. η цикла, а также теплоту Q2, которую газ отдает охладителю при изотермическом сжатии.
2.35. Совершая цикл Карно, газ получил от нагревателя теплоту
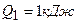 и совершил работу
и совершил работу 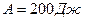 . Температура нагревателя
. Температура нагревателя  . Определить температуру T2 охладителя.
. Определить температуру T2 охладителя.
2.36. Газ, совершающий цикл Карно, получает от нагревателя теплоту  . Какую работу совершает газ, если абсолютная температура Т1 нагревателя в три раза выше, чем температура T2 охладителя?
. Какую работу совершает газ, если абсолютная температура Т1 нагревателя в три раза выше, чем температура T2 охладителя?
2.37. Совершая цикл Карно, газ отдал охладителю 2/3 теплоты, полученной от нагревателя. Определить температуру охладителя, если температура нагревателя 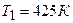 .
.
2.38. Газ совершает цикл Карно. Температура охладителя  . Какова температура нагревателя, если за счет каждой килокалории теплоты, полученной от нагревателя, газ совершает работу
. Какова температура нагревателя, если за счет каждой килокалории теплоты, полученной от нагревателя, газ совершает работу 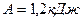 ?
?
2.39. Идеальная тепловая машина, работающая по циклу Карно, получает за каждый цикл от нагревателя 600 кал. Температура нагревателя
400 К, температура охладителя 300 К. Найти работу, совершаемую машиной за один цикл, и количество теплоты, отдаваемое охладителю за один цикл.
2.40. Идеальная тепловая машина работает по циклу Карно. При этом 80% тепла, получаемого от нагревателя, передается охладителю. Количество теплоты, получаемое от нагревателя, равно 1,5 ккал. Найти: 1). к.п.д. цикла;
2). работу, совершенную при полном цикле.
ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
